OM PARAMETERFREMSTILLINGER OG BUELÆNGDE

Parameterfremstillinger og buelængde

1. Parameterfremstillinger

Når man skal beskrive en kurve i et koordinatsystem, er en af mulighederne, at kurven er grafisk billede af en funktion y = f(x). Der er imidlertid ikke så mange kurver, der kan beskrives på denne måde. Det kræver jo, at en lodret linie kun skærer kurven i ét punkt. I stedet bruger man tit parameterfremstillinger, når man skal undersøge en kurves egenskaber. En parameterfremstilling er et udtryk som (x,y) = (f(t), g(t)). Når t varierer, eventuelt kun i et begrænset område, gennemløber (x,y) en kurve med den angivne parameterfremstilling. Lad os f.eks. tage parameterfremstillingen (x,y) = (cost, sint). For enhver værdi af t vil (x,y) opfylde ligningen x² + y² = 1. Parameterfremstillingen fremstiller derfor enhedscirklen med centrum i (0,0). Hvis t varierer frit, gennemløbes cirklen uendelig mange gange. Hvis 0 ≤ t < 2π, gennemløbes cirklen præcis én gang.

Koordinatfunktionerne i parameterfremstillinger opfattes som koordinater for stedvektorer ud fra koordinatsystemets begyndelsespunkt.

Her følger nogle andre vigtige parameterfremstillinger:

(x,y) = (a + bt, c + dt) = (a, c) + t(b, d) fremstiller en ret linie gennem (a, c) med hældningskoefficient α = d/b.

(x,y) = (a + rcosωt, b + rsinωt) = (a, b) + r(cosωt + sinωt) fremstiller en cirkel med centrum i (a, b) og radius r. Hvis t betyder tiden, gennemløbes cirklen med konstant vinkelhastighed ω.

(x,y) = (acosωt, bsinωt) fremstiller en ellipse med centrum i (0,0) og halvakser a og b.

Man kan vise, at parameterfremstillingen

(x,y) = (acosωt + bsinωt, ccosωt + dsinωt)

fremstiller en ellipse, lige meget hvilke værdier konstanterne a,b,c,d og ω har. (Det kan dog også være et liniestykke eller et punkt).

Parameterfremstillinger er særlig vigtige, når man skal beskrive et punkts bevægelse i tidens løb. Så betyder t tiden.

Lad os som et eksempel tage Galileis kasteparabel, der fremkommer, når man kl. t = 0 kaster en grøn partikel fra punktet (0,h) med starthastighed v = (a, b). Accelerationen er konstant, nedadrettet og har størrelsen g. Partiklens koordinater til tidspunktet t betegnes (x(t),y(t)). Ifølge definitionen af acceleration er (x´´(t),y´´(t)) = (0, -g). Heraf fås ved integration, at (x´(t),y´(t)) = (a, − gt + b), hvor integrationskonstanterne er valgt, så begyndelseshastigheden bliver (a, b). Heraf fås ved endnu en integration, at
(x(t),y(t)) = (at, -½gt² + bt + h).

Denne parameterfremstilling for kasteparablen giver langt mere information end den sædvanlige ligning for parablen. Når vi har parameterfremstillingen, ved vi til ethvert tidspunkt, hvor partiklen er.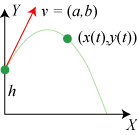

Animationen til venstre viser bevægelsen i et konkret tilfælde. Vi har valgt h = 15 mm, a = 2,5 mm/sek, b = 5 mm/sek og g = 5/6 mm/sek². Det sidste mærkelige tal skyldes at vi vil have pæne tal. Indsættes tallene, fås parablens parameterfremstilling, når x og y er målt i mm:
(x(t),y(t)) = (2,5·t, - 5/12· t² + 5t + 15), 0 ≤t ≤14,3 sek.

Parablen har toppunkt i punktet (15, 30), når vi måler i mm.

2. Buelængde

Ved integration kan man også finde buelængder. Selve formlen er god nok, men det integral, der indgår, er i mange tilfælde svært at udregne, og der er endda mange tilfælde, hvor integralet ikke kan udregnes ved hjælp af de almindelige kendte funktioner.

Vi vil finde længder af buer på en kurve med parameterfremstillingen (x,y) = (x(t),y(t)), hvor t er en parameter, der gennemløber et eller andet interval. Når t gør det, vil punktet (x,y) gennemløbe en kurve, som man orienterer med en pil. Det skal være sådan, at når t vokser, bevæger punktet (x,y) sig i pilens retning. En bue fra A:(x(t₁), y(t₁)) til B:(x(t₂), y(t₂)) på kurven har så positiv længde, når t₂ > t₁, ellers er længden negativ.

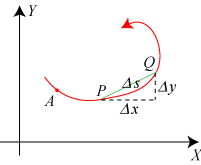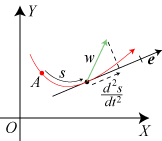
Vi vælger nu et fast punkt A:(x(t_o), y(t_o)) på kurven, og så vil vi beregne buelængden s hen til punktet P:(x(t, y(t)). Det gør vi ved først at udregne differentialkvotienten s´(t). Derfor giver vi t en lille tilvækst Δt. Så får x, y og s tilvækster, som vi betegner Δx, Δy og Δs, som alle tre er vist på figuren. På figuren er det uklart, om Δs er længden af den røde bue eller længden af den grønne korde. Og det er også lige meget. For om lidt lader vi Δt gå mod 0, og så vil forholdet mellem bue og korde gå mod 1. Af Pythagoras fås, at

Δx² + Δy² = Δs².
Så dividerer vi med Δt²: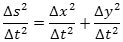

Lader vi nu t→0, får vi en ligning mellem de tre differentialkvotienter:

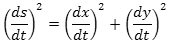
For at få nogle overskuelige formler går vi nu over til at bruge Newtons betegnelse for differentialkvotient: Når han satte en prik over funktionsnavnet, betød det differentialkvotienten. Så får den sidste formel følgende udseende:

Da s er en voksende funktion af t, skal der intet minus foran rodtegnet. Vi kan nu finde s selv ved integration. Da s(t_o) = 0 bliver resultatet, at

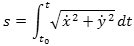
Som nævnt ovenfor er dette integral tit vanskeligt eller endog umuligt at udregne. Men vi tager et eksempel, hvor det kan lade sig gøre.

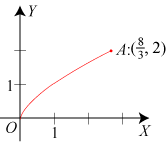Vi vil finde længden af den på figuren viste røde kurve. Den har parameterfremstillingen

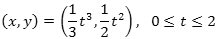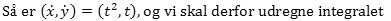
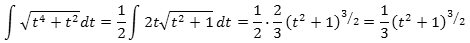
hvilket også kan regnes ud på en god lommeregner. Heraf fås så, at den søgte buelængde bliver

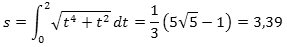
et resultat, der stemmer rimelig godt med figuren.

Til sidst vil vi finde et udtryk for s´´(t), som spiller en rolle i andre sammenhænge.

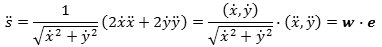Vi tænker os her, at t betyder tiden, så accelerationen er w: (x´´(t), y´´(t)). Ved differentiation af udtrykket for s´(t) fås, at

Her betyder e en enhedsvektor på tangenten, orienteret samme vej som kurven. s´´(t) er altså den med fortegn regnede længde af projektionen af w på tangenten.

Hvis du støder på et ord,
hvis betydning du ikke kender,
så søg på ordet.