Forside Søgning Liste

Polære koordinater

Et polært koordinatsystem i planen blev først beskrevet midt i 1600-tallet. Der var flere matematikere, der omtrent samtidig beskrev begrebet. Senere skrev Newton om polære koordinater i sin "Method of Fluxions" fra 1671, og i en artikel i tidsskriftet "Acta Eruditorum" fra 1691 beskrev Jacob Bernouilli polære koordinater. De kom begge så langt som til at beregne kurvers krumning i polære koordinater. Her beskriver vi polære koordinater i vor tids stil, især med henblik på at antyde, at Newton kan have brugt polære koordinater da han opdagede afstandskvadratloven.

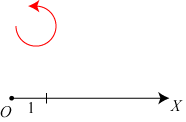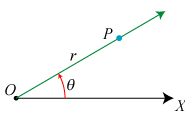Figuren ovenfor viser et polært koordinatsystem i planen. Det består af fire ting: Et begyndelsespunkt O, en orienteret X-akse gennem O, en længdeenhed på X-aksen og en rød orientering af planen. Normalt viser man kun de to første ting. Det er så underforstået, at planen orienteres mod uret, og at der er en enhed.	Et vilkårligt talpar (r,θ) er da polære koordinater for det punkt P i planen, som man finder således: Tegn den orienterede grønne linie gennem O, således at vinklen fra X-aksen til den grønne linie er θ radianer. P er så det punkt på den grønne linie, der ligger sådan, at den med fortegn regnede afstand fra O til P er r. På figuren er r ca. 5 og θ er ca. π/6, θ ≈ 0,52.

Når r og θ er givne findes der kun ét punkt med koordinater (r,θ). Men et punkt P har mange sæt polære koordinater. Man kan nemlig dels addere et multiplum af 2π til θ. Og man kan skifte fortegn på r, hvis man samtidig adderer π til θ. Denne ulempe ved polære kordinater viser sig at være uden større betydning.

Når man skal finde de polære koordinater til en vektor, skal man afsætte vektoren ud fra O. Vektorens koordinater defineres da som endepunktets koordinater.

Lad os nu betragte det vigtige tilfælde, hvor r og θ er funktioner af en variabel t, som vi kalder tiden, (r,θ) = (r(t),θ(t)). Så bevæger P sig i tidens løb på en blå kurve, og vi går nu over til at finde hastighedsvektoren og accelerationsvektoren for denne bevægelse.

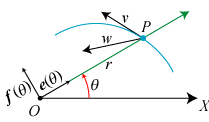Vi indfører de to enhedsvektorer e(θ) og f(θ). Hvis vi supplerer X-aksen med en lodret Y-akse får e(θ) koordinaterne (cosθ, sinθ) og f(θ) får koordinaterne (- sinθ, cosθ). Derfor bliver differentialkvotienterne mht. t Prik over er Newtons betegnelse for differentiation mht. tiden. Stedvektoren til P er OP = re. Hastigheden v fås heraf ved differentiation: og ved yderligere en differentiation fås, at accelerationen bliver

Disse formler får vi brug for, når vi skal vise, hvordan Newtons love for planetbevægelserne kan udledes af Keplers love ved regning i polære koordinater. Samme sted får vi brug for at kende en ellipses ligning i polære koordinater. Den kommer her:

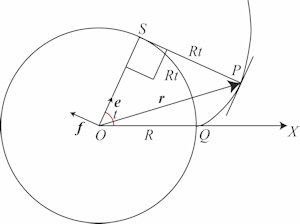
Vi betragter en ellipse, hvis storakse er 2a, og hvis excentricitet er e. Som vist på figuren til højre vælger vi et polært koordinatsystem med storaksen som X-akse og med begyndelsespunkt O i et af ellipsens brændpunkter. Man kan så bevise, at i dette polære koordinatsystem har ellipsen ligningen Beviset er lidt kompliceret, så vi nøjes med at bemærke, at for θ = 0 bliver r = a - ae, hvilket stemmer med figuren. For θ = π bliver r = a + ae, hvilket også er korrekt.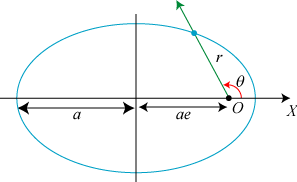

Der er mange problemer, som lettere løses i polære koordinater end i retvinklede. I listelinien 1686 om behandling af Keplers love i polære koordinater er der eksempler af denne art.

I 1762 offentliggjorde Leonhard Euler en meget hensigtsmæssig form på tænderne på tandhjul. I vores beskrivelse af Eulers konstruktion får vi brug for en egenskab ved en art kurver, som kaldes cirkelafviklere eller blot afviklere. Denne egenskab bevises lettest i polære koordinater, så derfor gennemgår vi den her.

Billedet til venstre viser, hvordan en afvikler konstrueres: Der er (med uret) viklet en snor rundt om cirklen på figuren. Snoren ender med et lille øje, der til en start befinder sig i punktet Q. Vi stikker spidsen af en blyant ned i øjet, vikler snoren af cirklen og holder hele tiden snoren stram. Kurven på figuren er så den kurve blyanten tegner, en afvikler. Vi vælger et tilfældigt punkt P på afvikleren og SP er så det afviklede stykke af snoren. Vinklen fra X-aksen op til OS kaldes t og måles i radianer. Det følger så af definitionen af en afvkikler at linjestykket SP har samme længde som buen SQ, nemlig Rt. Vi vil nu finde retningen af tangenten til afvikleren i punktet P. Ifølge formlen for v ovenfor, får man en vektor på tangenten ved at differentiere vektoren r på figuren mht t. Af figuren aflæses, at , og heraf fås ved differentation mht t, at Sensationen er nu at leddene med f hævede hinanden. Vi har altså vist følgende sætning: Afviklerens tangent i punktet P er vinkelret på linjen SP

Denne sætning er det bærende fundament under Eulers konstruktion af jævne tandhjul; læs mere i liste 3, år 1762.

Beviset for sætningen svigter, når t=0. Beviset kan føres ved at udregne hældningskoefficienten for linjen PQ, og dernæst finde dens grænseværdi for t→0, men det er ret besværligt. Resultatet er, at X-aksen er tangent til afvikleren i punktet Q.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.
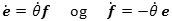
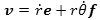
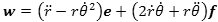
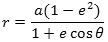
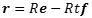