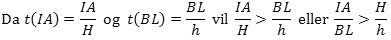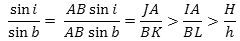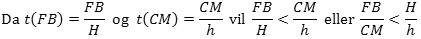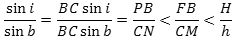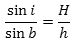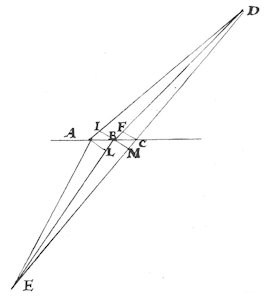
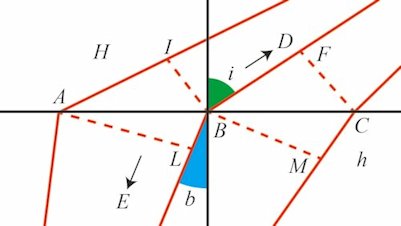
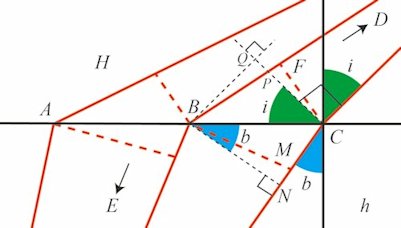
Den 27. november 1677 offentliggjorde Rømer et arbejde om lysets brydning. Fermats princip siger, at lyset på sin vej fra et punkt D til et punkt til et punkt E bevæger sig ad den hurtigste vej fra D til E. Specielt gælder dette også, hvis lyset på sin vej passerer en grænseflade mellem to forskellige materialer med forskellig lyshastighed. I sin afhandling udleder Rømer Snells brydningslov ved hjælp af Fermats princip. Vi beskriver her Rømers udledning i et moderne sprog - "moderne" matematisk set.

På figurerne herunder adskiller linjen AC to materialer. Over linjen AC er der et materiale, f.eks. luft, hvor lyshastigheden er H, og under linjen AC er der et andet materiale, f.eks. glas, hvor lyshastigheden h er mindre. Vi tænker os, at hvis lyset skal fra D til E, så er vejen DBE den hurtigste.

Rømers originale illustration til artiklen

Herover viser vi den centrale del af Rømers illustration i let ændret og forstørret udgave. De punkterede linjer er tegnet så DI = DB, DF = DC, EA = EL og EB = EM. Der er altså 4 langstrakte ligebenede trekanter på figurerne. Vinklerne ved grundlinjerne er < 90°. Fire gange bruger vi i argumenterne nedenfor, at to vinkler er lige store, hvis højrebenene er vinkelrette på hinanden, og venstrebenene er vinkelrette på hinanden Når vi skriver f.eks. BL mener vi længden af linjestykket, og hvis vi skriver t(BL) mener vi den tid, som lyset er om at komme fra B til L. På figurerne nedenfor er de punkterede sorte linjestykker tegnet så de viste vinkler er rette.

Her undersøger vi strålen DAE. Da t(DAE) > t(DBE) vil t(IA) > t(BL). Dette skyldes, at DI = DB og AE = LE. Videre fås, at

Her undersøger vi strålen DCE. Da t(DCE) > t(DBE) vil t(CM) > t(FB). Dette skyldes, at DF = DC og EB = EM. Videre fås, at

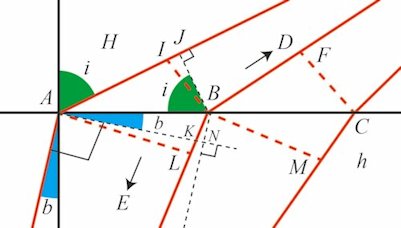
Hvis man lader punktet A glide hen mod punktet C ser man, at forholdet mellem de to sinusser ved passagen af punktet B vil skifte fra at være større end hastighedsforholdet til at være mindre end hastighedsforholdet. Derfor vil det for den øverste figur gælde, at

og dette en netop Snells brydningslov, endda i Huygens´ version.

Tankegangen i beviset ovenfor følger nøje Rømers egen fremstilling. Men udtryksmåden er forskellig fra Rømers. Rømer skriver ingen formler, han baserer sig hele tiden på "forhold", og det gør det vanskeligt at følge hans fremstilling. Siden græsk oldtid havde man talt om forhold i stedet for om tal. Rømer levede i en periode, hvor man gik over til at bruge tal og udtrykke sammenhænge i algebraiske formler. Selv om mange mennesker ikke kan lide formler, så er det faktisk sådan, at formlerne øger forståeligheden.

Vi viser en oversættelse til dansk af Rømers originale artikel her. Kilden til oversættelsen kan ses i referencerne.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.