Forside Søgning Liste

Optik

Scheiner opdagede, at øjets evne til at akkommodere, dvs stille skarpt, kommer i stand derved, at nogle muskler rundt om øjets linse kan ændre linsens krumning og derved tilpasse brændvidden, så der dannes et skarpt billede på nethinden af det objekt, som opmærksomheden er henledt på.

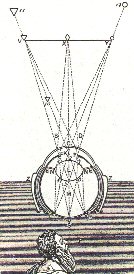
Figuren ovenfor viser Descartes opfattelse af strålegangen i et øje. Ved NE og EN aner man de muskler, der kan ændre linsens krumning. Scheiner brugte ved sine undersøgelser øjne fra dissekerede lig. Han skrællede forsigtigt det yderste af bagvæggen af øjet, og kunne så bagfra se det billede, som øjets brydende system danner på nethinden. Billeddannelsen sker i det væsentlige ved lysets overgang fra luft til hornhinde. Øjets linse giver kun en mindre men vigtig korrektion af den samlede brydning. Scheiner blev også klar over, at det er nethinden, der er den lysfølsomme del af øjet.

Astronomi

På skærmen opdagede Scheiner solpletter, uafhængigt af Galileis opdagelse. Iagttagelsen blev første gang gjort den 21. marts 1611 sammen med Scheiners elev Johann Baptist Cysat. Skærmen gjorde det let at tegne pletterne ind på et billede af solskiven. På den måde opdagede de, at pletterne bevæger sig, og som de første iagttog de, at pletterne nær Solens ækvator (i ekliptikas plan) bevæger sig hurtigere end pletter længere væk fra ækvator. Scheiner, der var jesuit, fortalte om opdagelsen til en højerestående ordensbroder. Han fik omgående besked på at holde kæft med sin opdagelse med den begrundelse, at den for det første stred mod Solens renhed, og for det andet at Aristoteles ikke havde beskrevet en sådan forurening af Solen. Scheiner fortsatte dog arbejdet og bestemte ved sine studier af solpletter retningen af Solens omdrejningsakse og Solens omdrejningshastighed.

På baggrund af Keplers beskrivelse i sin bog Dioptrik fra 1611 konstruerede Scheiner i 1613 (som den første?) en astronomisk kikkert.

Pantografen

En pantograf er et mekanisk instrument. Det kan bruges til at forstørre eller formindske stregtegninger. Du kan se Scheiners egen tegning af en pantograf i vores biografi, klik på Liste øverst her på siden. Til højre kan du se et eksempel, hvor en pantograf forstørrer billedet af en halvcirkel 3 gange. Pantografen består af 4 stænger, 2 røde og to blå. Stængerne omkranser et parallellogram, og den øverste røde stang stang kan dreje sig om det sorte punkt øverst til venstre. Når man skal bruge pantografen tager man f.eks. fat i det nederste punkt af den lange blå stang. Så bevæger man dette punkt sådan, at spidsen af den korte røde stang følger den stregtegning, som skal forstørres. Under bevægelsen bevares parallellogrammets sidelængder. Også længderne ef den lange røde stang og den lange blå stang er konstante.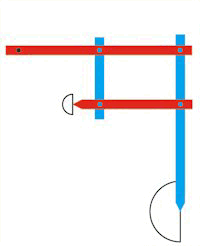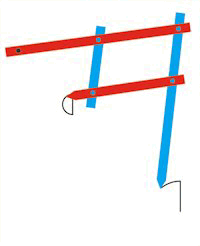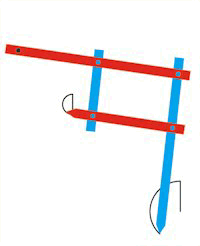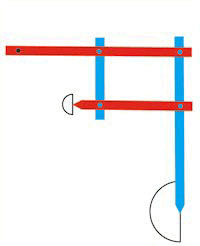

Vi går nu over til at bevise, at pantografen virker. Vi bruger det taleksempel, som er brugt i animationen, altså de stanglængder, der står på figuren til højre. Argumenterne kan uden videre bruges i andre taleksempler, og også hvis man bruger bogstaver i stedet for tal. Det er afgørende, at stængerne danner et parallellogram med konstante sidelængder. På animationen kan man se, at den punkterede linje OQ drejer sig uregelmæssigt under bevægelsen, og man ville derfor ikke forvente, at afstanden DE skulle være konstant under bevægelsen. Det er ikke så svært at vise, at afstanden DE faktisk er konstant, men kun et meget kreativt menneske kan få den ide, at når stængerne er koblet sådan sammen, så er afstanden DE konstant. Så vi sender Scheiner en lykønskning med tilbagevirkende kraft.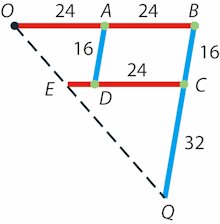

Her kommer så beviset for, at DE er konstant under bevægelsen:
De to trekanter OBQ og ECQ er ensvinklede. På den lange blå linje kan man se, at længderne af siderne i den lille trekant er ⅔ af længderne af de tilsvarende sider i den store trekant. Derfor gælder at EC = ⅔·48 = 32, og så må ED have længden 8 under hele bevægelsen. Det forholder sig altså sådan, at det faste punkt O, den venstre ende E af den korte røde stang og punktet Q ligger på en ret linje, den som vi har tegnet punkteret. Dette faktum er meget overraskende.

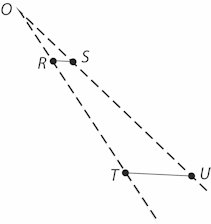Vi lader nu punktet E bevæger sig på en figur, som f.eks, kunne være den lille halvcirkel på animationen. Under denne bevægelse beskriver punktet Q en anden figur, som kunne være den store halvcirkel. Vi vil vise, at denne figur fås af den lille ved 3 ganges forstørring. Vi betragter to vilkårlige tidspunkter under bevægelsen. På figuren til venstre har vi tegnet stillingerne af den punkterede linje til de to tidspunkter. Vi vælger så til de to tidspunkter to vilkårlige punkter R og S på den lille figur. T og U er de punkter, hvor den nederste ende af den lange blå stang befinder sig på de valgte tidspunkter. Af ensvinklede trekanter på figuren ovenfor følger det at OT = 3·OR og OU = 3·OS. De to trekanter ORS og OTU er derfor ensvinklede, det vidste allerede Euclid. Derfor er TU = 3·RS. Alle afstande på den store figur er altså 3 gange så store som de tilsvarende afstande på den lille figur, og derfor fås den store figur af den lille ved 3 ganges forstørring

Pantografen blev i århundreder brugt ved løsning af mekaniske problemer. Lad os forestille os at en kunstner havde udarbejdet en tegning en af ny mønttype. For at få en formindsket udgave af tegningen kunne man anbringe tegningen nede ved spidsen af den blå stang, og man kunne lægge en lille messingplade der, hvor den formindskede kopi skulle være, dvs i nærheden af spidsen af den korte røde stang. Og i den spids kunne man så fastgøre en lille spids nål. Når man dernæst følger kunstnerens store tegning med den blå spids, så vil nålen ridse en formindsket kopi i messingpladen. Stanglængderne skulle så vælges sådan, at man at man får en kopi i den ønskede størrelse.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.