Forside Søgning Liste

I 1673 begyndte Huygens at studere det, man kalder sinusformede eller harmoniske svingninger. Der er tale om en bestemt type svingninger, som udføres af et punkt eller en partikel, der bevæger sig frem og tilbage på en ret linie. Her forklarer vi i nutidens matematiske sprog, hvad det er for nogle svingninger, og vi definerer de vigtige begreber, som er knyttet til dem. Vi vender senere tilbage til dem i fysikken (se bl.a. under 1664 Hooke og 1677 Bølgebevægelse).

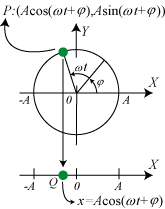På figuren viser vi øverst et grønt punkt P, der bevæger sig jævnt rundt på en cirkel med radius A. Til tidspunktet t har vinklen fra X-aksen til OP størrelsen ωt+φ, hvor ω og φ er konstanter. Nedenunder viser vi det grønne punkts projektion Q på X-aksen. Til tidspunktet t er afstanden x = OQ = Acos(ωt+φ). I tidens løb bevæger Q sig frem og tilbage på X-aksen. Denne bevægelse kaldes en harmonisk svingning eller en sinusformet svingning. A kaldes svingningens amplitude, ω kaldes dens vinkelfrekvens og φ dens fase. Svingningen kaldes sinusformet, selv om det er en cosinus, der indgår i definitionen. Da sin v = cos (v−π/2), kunne vi i formlen ovenfor lige så godt have skrevet sinus i stedet for cosinus.

Vi illustrerer begrebet harmonisk svingning med animationen nedenfor, hvor de tre farvede punkter forneden udfører harmoniske svingninger. Punkterne foroven udfører jævne cirkelbevægelser, og ved projektion på en ret linie fås en harmonisk svingning.

Konstanten A kaldes som nævnt svingningens amplitude. For alle de tre svingninger på figuren er A = 15 mm, men det kan nu afhænge lidt af din skærms opløsning. Det røde og det grønne punkt er 18 sekunder om en hel svingning. Det kaldes svingningstiden. Da funktionen x =  Acos(ωt+φ), har periode 2π/ω er 2π/ω = 18 sek. Derfor er vinkelfrekvensen for den røde og den grønne svingning ω = π/9 sek⁻¹ = 0,35 radianer pr sekund. Det blå punkt bruger kun 9 sekunder på en svingning. Det har derfor vinkelfrekvensen ω₁ = 2π/9 sek⁻¹ = 0,70 radianer pr sekund.

Konstanterne A og ω kan altså bestemmes, når man kender bevægelsen. Sådan er det ikke med konstanten φ. Den kan man først bestemme, når man ved, hvornår uret er startet. For svingningerne på animationen gælder følgende:

Når det røde punkt er i højre yderstilling for t = 0, beskrives svingningerne således:

RØDT PUNKT	GRØNT PUNKT	BLÅT PUNKT
x = Acos ωt	x = Acos(ωt−π/4)	x = Acos ω1 t

Når det grønne punkt er i højre yderstilling for t = 0, beskrives svingningerne således:

RØDT PUNKT	GRØNT PUNKT	BLÅT PUNKT
x = Acos(ωt+π/4)	x = Acos ωt	x = Acos (ω1 t+π/4)

Læg mærke til, at selv om fasen for en harmonisk svingning ikke kan bestemmes ud fra bevægelsen alene, så er faseforskellen mellem to harmoniske svingninger med samme svingningstid bestemt af de to bevægelser. F.eks. er differensen mellem det røde punkts fase og det grønne punkts fase π/4, fordi det røde punkt er vinklen π/4 foran det grønne; det ses lettest på cirkelbevægelserne.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.