| Ind til listen: |
Snells arbejder med brydningsloven og prismer
1. Brydningsloven
Cleomedes var vist den første, der skrev om lysets brydning, dvs. den ændring af retningen, der sker
med en lysstråle, når den går fra ét gennemsigtigt legeme til et andet. Cleomedes brugte brydningen
som forklaring på et astronomisk fænomen, men brydningen spiller en rolle i mange andre sammenhænge.
Selve den lov, som man bruger til at beregne brydningen med, blev imidlertid først fundet af Snell i
1621.
Lad os starte med at kigge på en lysstråle, der går fra luft ned i vand:
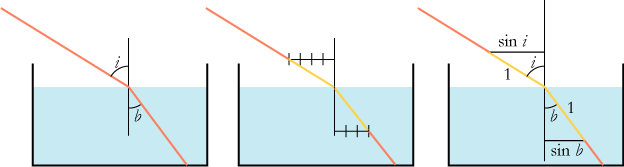
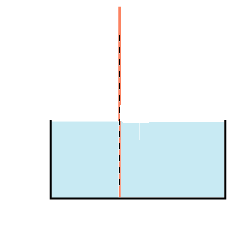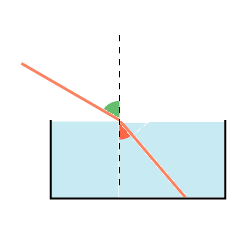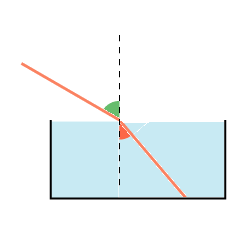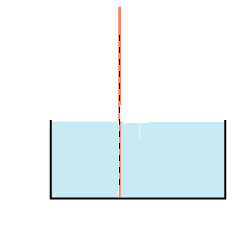
På figuren til venstre ser man en lysstråle, der rammer en vandoverflade i et punkt. I det punkt har vi tegnet en lodret linie. Den kaldes indfaldsloddet. Læg mærke til, at lysstrålen nede i vandet afbøjes ind mod indfaldsloddet. Strålen bliver efter afbøjningen i skærmens plan, den bøjes hverken udad eller indad. Snell fandt, at afbøjningen bestemmes af det såkaldte brydningsforhold n, der afhænger af, hvilke to stoffer lysstrålen går igennem. Ved overgangen fra luft til vand er brydningsforholdet 4/3. Hvad det betyder, kan man se på figuren i midten: Man afsætter to lige lange stykker på strålen fra vandoverfladen og i begge retninger. Det er de to lyse stykker. De to vandrette stykker fra enderne af det gule og ind til indfaldsloddet, skal så forholde sig som 4 til 3, sådan som det er vist på figuren. Når der er tale om overgang fra luft til vand, skal forholdet 4/3 anvendes hver gang, uafhængigt af indfaldsvinklens størrelse. Snell vidste det ikke, men faktisk skal brøken 4/3 ændres lidt, efter hvilken farve lyset har. Erfaringen viser, at strålegangen kan vendes, så hvis strålen kommer nede fra vandet og går op i luften, da bliver brydningsforholdet 3/4. På figuren til venstre kan du se, at hvis lysstrålen kommer nede fra, så bliver den afbøjet ned mod vandoverfladen.
Figuren ovenfor til højre illustrerer, at hvis brydningsforholdet ved overgang fra et stof til et andet
er n, da er sammenhængen mellem indfaldsvinklen i og brydningsvinklen b givet
ved brydningsformlen
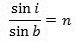
For Snell var formlen en erfaringssag. Han kendte ikke sammenhængen mellem brydningsforholdet n på den ene side. og de to stoffers fysiske egenskaber på den anden. Det var først Huygens, der fandt ud af det.
Vi illustrerer nedenfor brydningen ved overgang mellem luft og vand med en animation. Efter behag kan man tænke sig, at strålen går oppefra og nedad eller nedefra og opad. Vi standser animationen et øjeblik for at illustrere, at strålen følger brydningsloven.
Hvis brydningsforholdet ved overgang fra stof 1 til stof 2 er n, vil brydningsforholdet ved overgang fra stof 2 til stof 1 være 1/n. Heraf følger, at når en lysstråle passerer gennem en glasplade, der er lige tyk over det hele, da parallelforskydes strålen, men den skifter ikke retning:
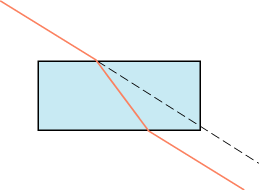
Af figuren ser man, at hvis glaspladen er tynd nok, kan man se bort fra parallelforskydningen, og strålen går da ubrudt gennem glaspladen.
En af grundene til, at det var svært at finde brydningsloven, kan være, at det er naturligt først at prøve at finde ud af, hvordan afbøjningsvinklen v afhænger af indfaldsvinklen i:
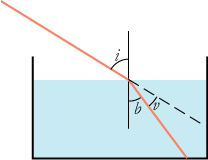
Sammenhængen mellem i og v er imidlertid så kompliceret, at man ikke kan finde den,
før man har brydningsloven. Sammenhængen er, at
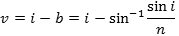
og det er jo ikke noget, man lige kommer på! Det her er et eksempel på, at det er vigtigt at stille det rigtige spørgsmål.
Newton fandt senere ud af, at brydningsforholdet afhænger af lysets farve. I tabellen nedenfor angiver
vi brydningsforholdet for gult natriumlys ved overgang fra luft til en række forskellige stoffer. (Se lyset
ved at drysse lidt salt i en gasflamme).
| Stof | Kvartsglas | Let kronglas | Let flintglas | Tungt flintglas | Diamant | Vand |
|---|---|---|---|---|---|---|
| Brydningsforhold | 1,46 | 1,51 | 1,61 | 1,75 | 2,42 | 1,33 |
Det spiller en afgørende rolle ved konstruktion af sammensatte linser, at de forskellige typer glas har forskellige brydningsforhold.
Hvis en stråle går fra vand til luft, så bestemmes brydningsvinklen af formlen
Hvis man her vælger en indfaldsvinkel i tæt på 90°, bliver sin b tæt ved 4/3, og det er jo umuligt. Snell synes ikke at have undersøgt dette paradoks, men det gjorde Kepler.
| Opgave 2 Forklar hvad der foregår på billedet ovenfor. |
2. Brydning i prismer
Vi går nu over til at omtale brydning i et prisme, f.eks. et glasprisme med trekantet tværsnit. Det, vi skriver her, er vist ikke fundet af Snell.
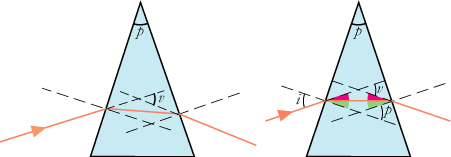
Figuren til venstre viser et glasprisme og en lysstråle i skærmens plan, der passerer to af prismets sideflader. De to flader skærer hinanden i prismets brydende kant, som vinkelret på skærmen går gennem prismets øverste punkt. Størrelsen af vinklen foroven kaldes p, den kaldes prismets brydende vinkel. Den samlede afbøjningsvinkel kaldes v. v er summen af de to afbøjninger, som strålen får ved de to passager fra luft til glas og omvendt. Læg mærke til, at ved overgangen fra luft til glas bøjes strålen ind mod indfaldsloddet, men ved overgangen fra glas til luft brydes strålen væk fra indfaldsloddet. I almindelighed er det kompliceret at udregne afbøjningen, men i det specielle tilfælde, som er vist til højre, hvor strålegangen er symmetrisk, er det ret let. Lad r betegne størrelsen af en rød vinkel og g størrelsen af en grøn vinkel. Så er indfaldsvinklen til venstre i = r+g, og brydningsvinklen er g. Hvis n er brydningsforholdet ved overgang fra luft til glas, siger brydningsformlen altså, at
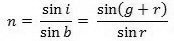
De to røde vinkler er tilsammen v, og de to grønne vinkler er tilsammen p. Derfor er
r = v/2 og g = p/2, og alt i alt får man derfor formlen
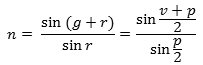
Denne formel er god til bestemmelse af brydningsforholdet n, den kræver nemlig kun måling af p og den samlede afbøjning v.
Under omtalen af linser får vi brug for et meget specielt tilfælde af denne formel: Det er det tilfælde,
hvor prismet er meget spidst, altså hvor p er lille, og hvor strålen ikke afviger ret meget fra
indfaldsloddet, altså hvor i og derfor r og g er små. Hvis vinklerne måles i radianer,
kan vi så erstatte sinus til vinklen med vinklen, og man får så, at
n=½(v+p)/½p = v/p + 1, eller v = (n-1)p
Denne formel kan bruges ved bestemmelse af styrken af en linse, sådan som vi skal se i omtalen af linser.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |
