|
Forside
Søgning
Liste |  |
Snells triangulering
Triangulering betyder opdeling i trekanter. Det var i gamle dage det vigtigste hjælpemiddel,
når man skulle lave landkort. I årene efter 1615 skete der et afgørende fremskridt inden for
triangulering. Metoden blev foreslået
af den hollandske matematiker Rainer Gemma Frisius allerede i 1533, men det var Snell,
der først udviklede metoden til
praktisk brug.
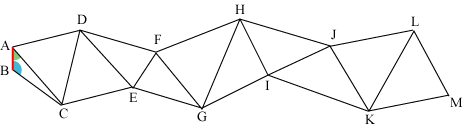
Ideen er, at man vælger to punkter A og B beliggende bekvemt i terrænet og måler afstanden mellem A og B med så stor nøjagtighed som muligt. Så vælger man et højt beliggende punkt C i omegnen og måler den grønne og den blå vinkel. Så kender man en side og to vinkler i trekant ABC, og derfor kan man regne ud, hvor lange siderne AC og BC er. Bagefter sigter man fra A og C mod D og udregner AD og CD. Ved at fortsætte sådan kan man udregne alle siderne på figuren, og til slut kan man regne de afstande ud, som man ønsker at bestemme, f.eks. DM.
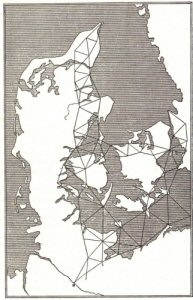
Ved trianguleringen af Danmark i 1800-tallet var AB en 2,5 km lang strækning på Amager, mens trekantsiderne i det store net af trekanter
var ca. 25 km lange. Den danske triangulering var knyttet sammen med den svenske og den tyske. Billedet nedenfor viser den
overordnede danske triangulering i 1800-tallet.
Der er klart, at et godt vinkelmåleinstrument var nødvendigt for at udføre trianguleringen. Til målingen benyttede man
det
instrument, som senere blev kaldt en teodolit. Med en teodolit kan man måle vinkler både i en vandret og i en lodret plan.
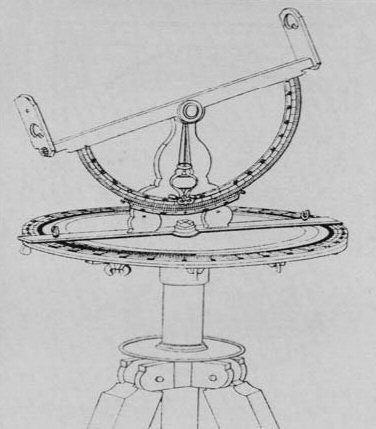 |
Tegningen viser den ældste teodolit, som vi har kunnet finde et billede af. |
Snell benyttede sig formodentlig af et instrument, der minder om det på figuren ovenfor. Som det ses, kan man ved at rette sigtelinealen mod et fjernt punkt aflæse en retningsvinkel på den vandrette gradskala. Sigter men derefter mod et andet punkt og aflæser vinklen, er vinklen mellem de to sigtelinier differensen mellem de to aflæsninger. Man gik nok ret hurtigt over til at bruge en kikkert i stedet for en sigtelineal.
Som man kan se på tegningen, kan man også på den lodrette gradskala aflæse, hvor meget linealen hælder. Hvis der er mærkbare højdeforskelle, må man tage hensyn til sigteliniernes hældning ved beregningen. Ved større opgaver må man også tage hensyn til Jordens krumning.
Snell benyttede bl.a. triangulering til at bestemme, hvor langt der er mellem to breddecirkler, f.eks. 57° og 58°.
Det skal jo (ifølge definitionen af en meter) give 111, 111 km, men vi har ikke kunnet finde ud af, hvor godt Snells resultat var.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |