Forside Søgning Liste

1. Historien om en soldat

Der kom et kompagni soldater marcherende hen over en græsmark. De gik fremad i række og geled. Rækkerne var på langs, og geledderne på tværs, og de var vinkelrette på hinanden. Geleddene var skiftevis røde og blå; det så godt ud. De gik 7 kilometer i timen, og det var onsdag. Så kom de til en pløjemark. Der kunne de kun gå 4 kilometer i timen. "Ligeud," råbte sergenten, "og hold række og geled." Det gjorde de, så godt de kunne, men geledderne blev skæve:

Det blev sergenten sur over, så næste dag lød kommandoen: "Når I kommer til pløjemarken, går I stik syd, og hold geleddene!" Den besked forstod soldaterne, for markskellet gik øst-vest. Men igen blev geledderne skæve.

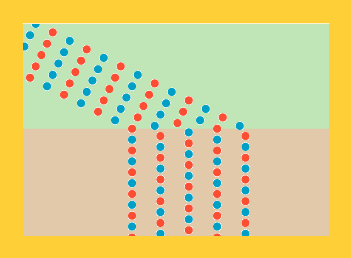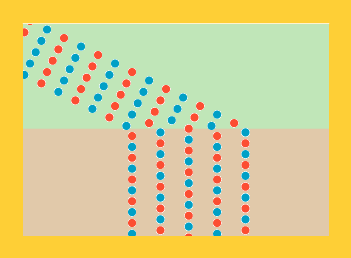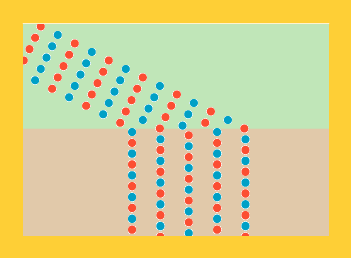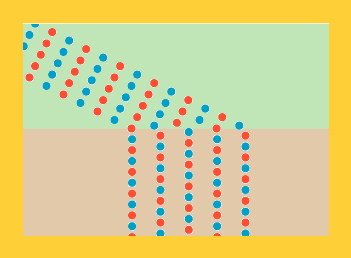
Men så var der en rød soldat ude i højre række - altså til venstre på figurerne - der hed Christiaan. Han er tegnet gul på figurerne nedenfor.

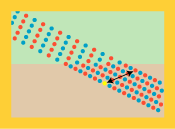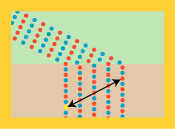Onsdag	Torsdag

Christiaan lagde mærke til, at om onsdagen var det sådan, at når alle i hans geled var kommet ud på pløjemarken, så var han selv længere tilbage end de andre i geleddet. "Det er jo logisk," sagde han til sig selv, "jeg var jo den første, der begyndte at gå langsomt." Men om torsdagen var Christiaan også den første i sit geled, der kom ud på pløjemarken. "Det var ligegodt satans," tænkte han, da han opdagede, at da de andre i hans geled også var kommet ud på pløjemarken, da var han længst fremme i sit geled. Han fandt hurtigt ud af, hvorfor onsdagslogikken ikke virkede om torsdagen. Kan du også finde ud af det, kære læser?

Og så tænkte Christiaan: "- når jeg er bagerst i geleddet, når vi går ligeud, og når jeg er forrest, når vi går mod syd, så må der næsten være en marchretning derimellem, hvor geleddene også på pløjemarken er vinkelrette på marchretningen." Og så tegnede han en forstørret udgave af det lille hjørne af kompagniet i det øjeblik, han selv nåede frem til pløjemarken:

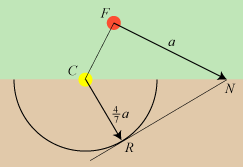
Christiaan, C, er selv gul på figuren. Hans gelednabo hed Frederik, F, han er rød på figuren. Og så tænkte Christiaan sådan: "Når Frederik om lidt er nået ned til pløjemarken i punktet N, har han gået en afstand, som vi kalder a. På det tidspunkt har jeg gået afstanden ⁴/₇ a, så jeg må være et eller andet sted på den sorte halvcirkel. Og det gælder så om at vælge et punkt R på halvcirklen, der ligger sådan, at Frederik og mig også på det tidspunkt danner geled vinkelret på den nye marchretning. Det punkt finder man frem til ved at tegne den tangent til halvcirklen, der går gennem N. R er så røringspunktet, for så passer det, at RN er vinkelret på marchretningen CR. Og hvis vi så til sidst lader beskeden om den nye marchretning gå videre hen langs geleddet, ja, så kommer det om fredagen til at passe hele vejen igennem."

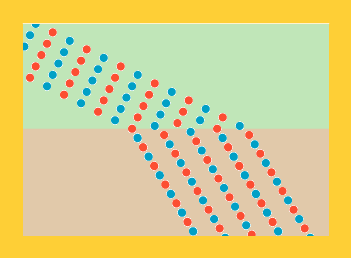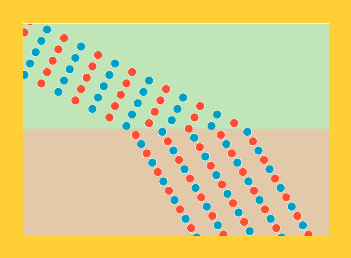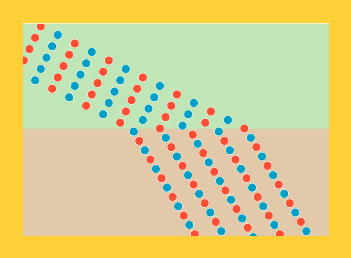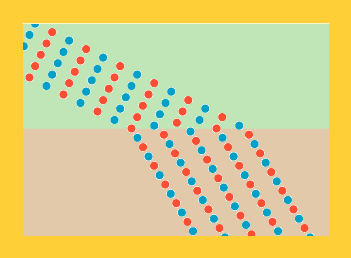
Da sergenten så, hvor fint det gik, blev han glad. "Slut for i dag," sagde han, "og hav en god weekend!"

Nu har vi lavet en geometrisk konstruktion af den nye marchretning. Til sidst vil vi vise, hvordan man kan udregne retningen:

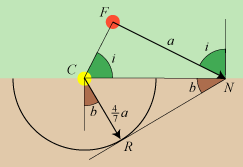
Vi skal først kende den retning, soldaterne marcherer i på græsmarken. Den er bestemt af vinklen i, der findes to steder på figuren. i kaldes indfaldsvinklen. Det er vinklen mellem marchretningen og en linie vinkelret på markskellet. Marchretningen på pløjemarken er bestemt af vinklen b. Den kaldes brydningsvinklen, og den findes også to steder på figuren. Af de to trekanter CNF og CNR fås, at

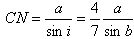
Brydningsvinklen kan derfor bestemmes af formlen

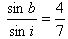
Hvis soldaterne går med hastigheden c₁ på græsmarken og med hastigheden c₂ på pløjemarken, fås med samme argument, at

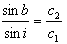
Det er tankevækkende, at denne formel minder om Snells formel for lysets brydning ved overgang fra et materiale til et andet. Den første, der fandt denne formel var Christiaan Huygens.

2. Soldaten og brydningsforholdet

Lad os overveje, hvad der egentlig foregår. Lad os antage, at der er en masse tætstående små sorte soldater i hvert geled, så et geled faktisk er et liniestykke. Og vi tænker os, at vi vil bruge dette liniestykke til at illustrere en bølgefront i en lysbølge. Vi antager altså to ting:

1. Lyset er en bølgebevægelse med bølgefronter, der langt fra lysgiveren er plane, på figurerne rette liniestykker.
2. Lysbølgen bevæger sig vinkelret på bølgefrontens retning.

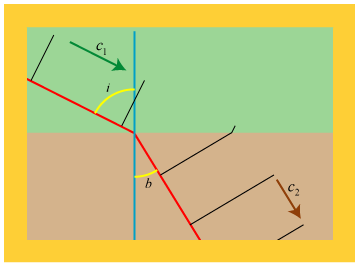
Det, vi ovenfor har vist, er følgende: Hvis vores lysbølge i et medium bevæger sig med konstant hastighed c₁, og hvis den passerer et plant, på figurerne retlinet, skel til et nyt medium, hvor hastigheden er c₂, da ændres bølgens bevægelsesretning i overensstemmelse med brydningsloven med brydningsforholdet n = ^c₁/c₂. Snells brydningsformel er altså en konsekvens af vores to antagelser. Og det er jo opmuntrende. Og mens Snell ikke udtalte sig om, hvilke egenskaber ved de to medier, der bestemmer brydningsforholdet, så medfører vores to antagelser altså, at brydningsforholdet er forholdet mellem lyshastighederne i de to medier. Og så er vi begejstrede: Vi har først og fremmest fået en klar fortolkning af begrebet brydningsforhold. Og yderligere er det et resultat, som før eller senere kan kontrolleres ved måling. Og omvendt, hvis den ene lyshastighed er kendt, kan man ved måling af en indfaldsvinkel i og en brydningsvinkel b bestemme den anden lyshastighed.

Vi ved ikke, hvornår argumentet med de marcherende soldater er opfundet, vi kender det fra La Cour. Men de to antagelser, som vi gjorde ovenfor, blev benyttet både af Huygens og Descartes.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.