Forside Søgning Liste

Torricelli og barometret

Vi bruger her ordet vakuum om det tomme rum, altså et rum uden atomer. Ordet blev brugt i denne betydning fra den græske oldtid og frem til arbejder af Torricelli (Kviksølvbarometret, 1644) og von Guericke (Sugepumpen, 1647). I oldtid og middelalder brugte man begrebet "horror vacui", "angsten for det tomme rum", som forklaringsmodel for en række fysiske iagttagelser.

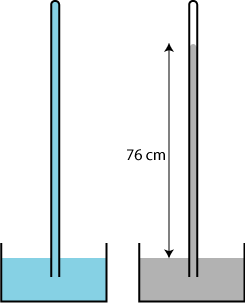Lad os tage et eksempel: Vi tager et meterlangt glasrør, der er lukket i den ene ende. Det fylder vi med vand, holder fingeren for den åbne ende og stikker hånden ned i et kar med vand, så bunden af glasrøret vender opad. Hvad mon der sker, hvis vi fjerner fingeren. Hvis vandet sank nedad i røret, ville der være vakuum foroven i røret. Men indtil den tid troede man ikke, at der kunne eksistere et vakuum. Troen kaldtes angsten for det tomme rum, "horror vacui". Og det passer med, at hvis vi fjerner fingeren, da ser vi, at alt vandet bliver oppe i røret. Torricelli opdagede fejlen i dette argument: Han erstattede vand med kviksølv, sådan som det er vist på figuren til højre. Nu var der ikke nogen horror vacui, der dannedes et tomt rum oppe over kviksølvet. Torricelli gav også den rigtige forklaring: Det er atmosfærens tryk på væskeoverfladen i skålen, der holder væsken oppe i røret. Denne ide virker helt naturlig i vore dage. Men dengang var den udtryk for en helt ny og meget fremmedartet måde at tænke på.

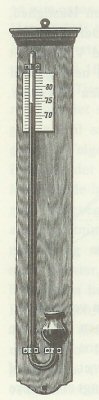Under sine forsøg med kviksølvsøjlen lagde Torricelli mærke til, at søjlens højde varierede lidt fra den ene dag til den anden. Torricelli var straks klar over, at det måtte skyldes variationer i atmosfærens tryk, og at fænomenet derfor måtte hænge sammen med vejrliget. Han havde opfundet barometret! På figuren viser vi, hvordan et kviksølvbarometer kunne være indrettet i gamle dage. Det består af et meterlangt glasrør, der er lukket i den øverste ende. I den anden ende er der en ombøjning, der ender i en udvidelse, der er åben opadtil. Før barometeret tages i brug, anbringes røret nogenlunde vandret, og man fylder den lange lige del og ombøjningen med kviksølv. Når man så løfter den tilsmeltede ende opad, dannes der et lufttomt stykke øverst i røret. Til sidst anbringes der en skala bag røret. Tallene angiver højdeforskellen mellem de to kviksølvoverflader, målt i cm. Man siger, at man måler trykket i cmHg, hvor Hg betyder kviksølv. Torricellis opdagelse var udgangspunkt for en helt ny opfattelse af lufthavet. Tidligere havde man troet, at verdensrummet var fyldt med luft, en opfattelse, der hang sammen med angsten for det tomme rum. Men efter Torricelli og især efter Pascals opdagelse i 1648 blev man klar over, at lufthavet ligger som et dække over Jorden og følges med Jorden i dens bevægelser. Et af de gamle argumenter for, at Jorden ikke bevæger sig, var, at hvis Jorden bevægede sig, ville her være et farligt blæsevejr. Denne betænkelighed ved Jordens bevægelse forsvandt med Torricellis og Pascals opdagelse.

Torricellis arbejde med kasteparabler

I fortsættelse af Stevins arbejder (1586) lavede Torricelli forsøg med et apparat som vist på figuren nedenfor:

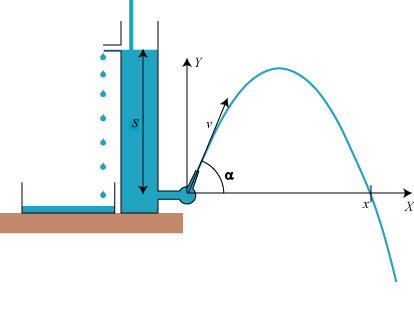
Ovenfra løber der vand ned i beholderen, og det øverste siderør sørger for, at der er konstant vandstand i beholderen. Vandet forlader så siderøret forneden i en smuk kasteparabel. Den var let at aftegne på en skærm bag parablen. Galilei havde fundet ud af, at hvis vandstrålens starthastighed er v, og strålens startretning danner vinklen α med vandret, da er skudvidden

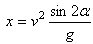
I formlen betyder x altså skudvidden, v betyder udstrømningshastigheden, og α betyder den vinkel, som starthastighedens retning danner med vandret. Her er vinklen α og tyngdeaccelerationen g kendte, og skudvidden x kan let måles. Derfor kan vandets starthastighed beregnes, og Torricelli fandt, at udstrømningshastigheden er uafhængig af vandstrålens startretning. Det er et resultat, der er beslægtet med et andet, som Stevin (1586) fandt: Han fandt, at trykket i et punkt nede i en væske i hvile er det samme i alle retninger. Men Toricelli tænkte videre: Når udstrømningshastigheden er uafhængig af skudretningen, så bør den jo være et eller andet udregneligt. Og Torricelli fandt, at hvis vanddybden ned til udstrømningsrøret kaldes s, da er udstrømningshastigheden

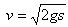
Ifølge en formel af Galilei (1600) er det præcis hastigheden af den vanddråbe, der befinder sig vandret ud for udløbsrøret. Et nydeligt resultat, ikke sandt!

Men Torricelli fandt ud af mere endnu. Han prøvede mange forskellige værdier af hældningsvinklen α og fandt frem til følgende billede:

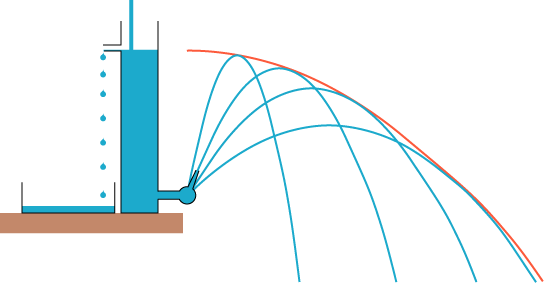
Her kunne han se, at lige oven over parablerne findes der en rød kurve, som alle parablerne rører nedefra. Denne røde kurve kaldes indhyllingskurve for kasteparablerne. Torricelli bestemte sig nu til at finde ud af, hvad den røde indhyllingskurve er for en. Vi bruger ikke Torricellis fremstilling, men bruger vor tids formelsprog.

For at svare på spørgsmålet skal vi bruge Galileis ligning for kasteparablen. Vi bruger det koordinatsystem, der er vist på figuren højere oppe. Ifølge Galilei er ligningen for kasteparablen

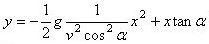
Her indsætter vi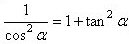

og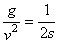

og får derved ligningen for kasteparablen på følgende bekvemme form:

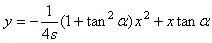
Den røde kurve rører altså alle de parabler, som fremstilles af denne ligning for forskellige værdier af α. For nu at løse problemet bruger vi den såkaldte "gad vidst-metode" og siger:

Gad vidst, om den røde kurve ikke skulle være parablen med ligningen

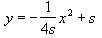
Det drejer sig nu om at bevise, at der findes et og kun et punkt (x,y), der passer i begge de to sidste ligninger. Vi ganger nu begge ligninger med 4s og trækker dernæst den øverste fra den nederste. Det giver, at

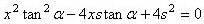
Pointen er nu, at her er venstre side kvadratet på en toleddet størrelse,

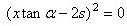
og den ligning er der kun én x-værdi, der passer i. nemlig

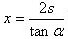
Den tilsvarende y-værdi bliver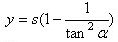

og derfor er punktet

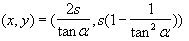
det eneste punkt, der ligger på begge parabler. Kasteparablen rører altså den anden parabel i dette punkt.

Så er problemet løst, men den opmærksomme læser vil nok undre sig over "gad vidst metoden". Hvor i alverden dukker den parabel op fra?? Her er det en ikke sjælden skik i matematik, at forfatteren holder overlæben stiv og antyder, at det jo ikke er forbudt at få en god ide. Det bliver læseren jo ikke meget klogere af, så nu skal vi fortælle, hvordan vi selv fik ideen. På figuren kunne den røde kurve godt ligne en nedadvendt parabel med toppunkt i punktet (x,y) =( 0,s). Og så kunne det se ud, som om den skærer X-aksen samme sted som 45° kasteparablen. På den måde fandt vi den mystiske ligning, og gættet viste sig altså at være rigtigt.

Resultatet af det hele er, at hvis man vil være sikker på ikke at blive våd af Torricellis springvand, så skal man holde sig over den røde parabel. Det samme gælder, hvis man vil være i sikkerhed for en af fjendens kanoner. Den røde parabel kaldes derfor en sikkerhedsparabel.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.