Forside Søgning Liste

Fra begyndelsen af 1600-tallet blev det mere og mere klart, at mange fysiske størrelser ikke kunne beskrives alene med en talværdi. Det kunne også være nødvendigt med en retning knyttet til den pågældende størrelse. F.eks. er en hastighed ikke velbeskrevet ved oplysningen om, at den er 50 km/t. Der mangler jo en oplysning om, hvad vej bilen kørte. Også begrebet kraft, som blev mere og mere veldefineret i løbet af 1600-tallet, beskrives kun ordentligt ved angivelse af såvel størrelse som retning. Dette behov for samtidig information om størrelse og retning førte til, at begrebet vektor langsomt blev klargjort. Begrebet er skabt af et behov i fysikken, men det er i sin natur rent matematisk. Vi beskriver det her i nutidens sprog, men gør opmærksom på, at det kun langsomt fik en fortjent plads i matematikken, en udvikling der i elementære fremstillinger stadig var igang omkring år 1900. Vektorer findes i både planen og rummet, men for overskuelighedens skyld lægger vi her størst vægt på at beskrive situationen i planen.

1. Definition og addition af vektorer

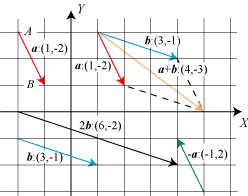En vektor defineres som et orienteret liniestykke, dvs. et liniestykke forsynet med en pil i den ene ende; men med den tilføjelse, at to sådanne vektorer regnes for at være ens, hvis den ene kan føres over i den anden ved en parallelforskydning, som fører enden med pil over i enden med pil. Enden med pil kaldes vektorens endepunkt, og den anden ende kaldes dens begyndelsespunkt. På figuren er de to røde vektorer ens, mens den grønne vektor er forskellig fra de røde. De to blå vektorer er også ens. Hvis liniestykket har længden 0, kaldes det nulvektoren og skrives 0. En vektor i XY-planen har et koordinatsæt (x,y). x er længden (regnet med fortegn) af vektorens projektion på X-aksen, og y er længden af dens projektion på Y-aksen. På figuren kan du se en række eksempler. Hvis man vil fremhæve, at en størrelse er et tal og ikke en vektor, kaldes den en skalar. Nulvektoren har koordinaterne (0,0).

Her navngiver vi vektorer med fede bogstaver, a, b, u, v, ..., og når vi skal angive koordinaterne skriver vi sådan, som det er vist på figuren. Hvis en vektor begynder i A og ender i B, betegnes vektoren AB. Hvis a er en vektor, betegnes længden ( ≥ 0) af liniestykket med a eller |a|. Hvis a:(x,y) gælder, at |a|=(x²+y²)^½, altså kvadratroden af kvadratsummen af koordinaterne. En vektor a:(x,y) kan multipliceres med en skalar k. Det gør man ved at multiplicere længden med |k| (som er ≥ 0). For k>0 beholdes retningen, og for k<0 skiftes til den modsatte retning. Figuren viser b og 2b samt a, og med grønt −1·a = -a. Hvis a:(x,y), vil ka:(kx,ky). To vektorer a og b kan adderes. Summen bestemmes ved, at man afsætter de to vektorer fra samme punkt. Summen a+b er da den vektor, der begynder i samme punkt som a og b, og som ender i det modstående punkt af det parallellogram, som a og b udspænder. Se eksemplet på figuren ovenfor. Såvidt vi ved, har denne definition af addition af vektorer sin oprindelse i kræfternes parallellogram. Når a:(x,y), og b:(u,v), er a + b:(x + u,y + v), sådan som det også let ses i eksemplet på figuren. Nu har udtryk som 3a − 4b +10c også mening.

2. Tværvektorer

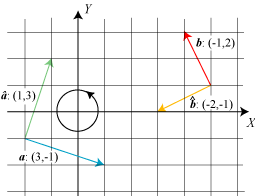
En vektor a i en orienteret plan har en såkaldt tværvektor, som betegnes â. â fås ved at dreje a 90° i orienteringens retning. Der er vist et par eksempler på figuren til højre. Hvis a:(x,y), vil â:(-y,x), en regel som man let overbeviser sig om ved at kigge på eksemplerne på figuren.

3. Skalarprodukt

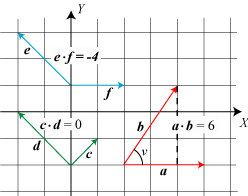Vektorer kan multipliceres på to væsensforskellige måder. Først omtaler vi skalarproduktet af to vektorer a og b. Dette produkt betegnes a·b, hvor prikken aldrig udelades. Produktets værdi er en skalar, nemlig tallet ab cosv, hvor v er vinklen mellem vektorerne, og a og b er deres længder. Man kan også sige, at skalarproduktet af to vektorer er den enes længde multipliceret med længden af den anden vektors projektion på den linie, som den første ligger på. Underforstået et minus, hvis vinklen mellem vektorerne er > 90°. Se eksemplerne på figuren. Et skalarprodukt er 0, både hvis en af faktorerne er 0, og hvis de to vektorer er vinkelrette på hinanden. Hvis a:(x,y) og b:(u,v) kan man vise, at a·b = xu+yv.

Her kommer et eksempel på anvendelse af et skalarprodukt: Lad os sige, at en konstant kraft K virker på en partikel, der bevæger sig fra begyndelsespunktet til endepunktet af en vektor AB. Så er det arbejde, som kraften udfører K·AB. Det er nemlig kun kraftens projektion på bevægelsesretningen, der spiller en rolle for det arbejde, som kraften udfører.

4. Vektorprodukt

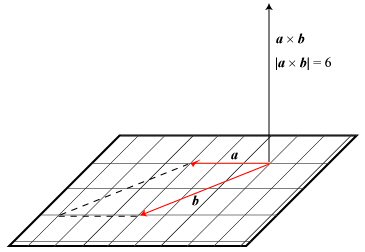Og nu skal vi så til sidst omtale begrebet vektorprodukt. Det er et begreb, der hører hjemme i rummet, så nu betragter vi to vektorer a og b i rummet. De har så et vektorprodukt, der skrives a×b. Vektorproduktet er en vektor, hvis længde er arealet af det parallogram, som vektorerne a og b udspænder, når de afsættes ud fra samme punkt. Retningen af a×b skal være vinkelret på den plan, som a og b ligger i, og så skal orienteringen af a×b vælges, så de tre vektorer a, b og a×b er i højrestilling. Det sidste betyder følgende: Orienter den nævnte plan i retning fra a til b. Drej en proptrækker vinkelret gennem den nævnte plan i orienteringens retning og samme vej rundt, som når du skal skrue den ned i en prop. Proptrækkeren peger så i den retning, som a×b skal orienteres. På figuren skal proptrækkeren komme nedenfra.

Begrebet vektorprodukt kan ved første øjekast virke noget sært og umotiveret. Her er et eksempel på brug af et vektorprodukt: Lad os sige, at der i et kort retlinet stykke ledning fra A til B går en strøm på i ampere. Vi er interesseret i at finde feltstyrken i et vilkårligt punkt P. Det bidrag til denne magnetiske feltstyrke, som stammer fra ledningsstykket AB, er da bestemt ved formlen F  = 0,1· i·AB×AP/r3, hvor r er afstanden AP. Det passer kun med retningen af strøm og feltstyrke, fordi vi i definitionen af vektorprodukt valgte højrestilling. Det må dog bemærkes, at definitionen af retning af en strøm og magnetisk feltstyrke er kulturelt bestemt, ikke fagligt. Det hænger bl.a. sammen med, at definitionerne blev formuleret af fysikere på den nordlige halvkugle. Man kan undre sig over faktoren 0,1 i formlen. Denne faktor skyldes, at strømenheden 1 ampere er defineret ud fra formlen ovenfor, læs nærmere om det under definitionen af strømstyrke.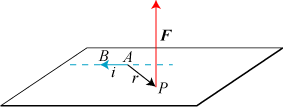

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.