Forside Søgning Liste

I linien om differentiation har vi forklaret, hvad differentialkvotienten for en funktion er. Her forudsætter vi, at det ved du. De funktioner, vi betragtede der, var af typen y = f (x). Her er både x og y reelle variable. Dvs. at de kan antage talværdier, der kan skrives som endelige eller uendelige decimalbrøker. Her skal vi beskrive differentiation af en anden slags funktioner, nemlig den, hvor den uafhængige variabel igen er et tal t, men hvor funktionsværdien er en vektor. Standardnavnet for en vektorfunktion er r = r(t). Her betyder t en reel variabel, mens funktionsværdien r = r(t) er en vektor i planen eller rummet. Grunden til, at man bruger navnet t for den uafhængige variabel, er, at t i mange anvendelser af vektorfunktioner betegner tiden. t behøver ikke at kunne antage alle værdier, typisk vil der være angivet et interval I, inden for hvilket t kan variere. Det er af afgørende betydning, at der til hver af de benyttede værdier af t kun findes én funktionsværdi r(t).

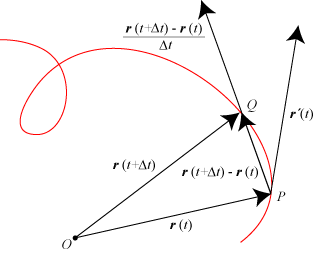Når man grafisk skal afbilde vektorfunktionen r = r(t), hvor t varierer i et interval I , behøver man i første omgang ikke et koordinatsystem, men bare et punkt O. For hver værdi af t tegner man så vektoren r(t), så den får begyndelsespunkt i O. Når man så lader t gennemløbe I voksende, vil endepunktet P af r(t) gennemløbe en rød kurve, og man kan opfatte vektorfunktionen r(t) som en beskrivelse af denne kurve, gennemløbet på en bestemt måde. Vi går nu over til at definere differentialkvotienten r´(t) af vektorfunktionen r(t). Først lader vi t være et bestemt tal, og det giver vi en tilvækst Δt. Så afsætter vi vektoren r(t+Δt) ud fra O. Dens endepunkt betegnes Q, og vektoren PQ er da differensen r(t+Δt) - r(t). Retningen af denne differens er da et bud på retningen af kurvens tangent i P, og hvis Δt er lille, er det et godt bud.

Nu kan man imidlertid ikke finde tangentretningen ved at se på, hvad vektoren PQ nærmer sig til, når Δt → 0. For så nærmer PQ sig nulvektoren. Derfor gør vi PQ længere ved at dividere den med det lille tal Δt. r´(t) defineres da som den vektor, som differenskvotienten nærmer sig ubegrænset til, når Δt → 0, altså

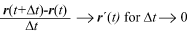
Hvis r´(t) ≠ 0, bestemmer den retningen af tangenten til kurven i punktet P. Det sker, men sjældent, at r´(t) = 0 for en enkelt værdi af t. Så kan man bruge højere afledede til bestemmelse af tangentretningen.

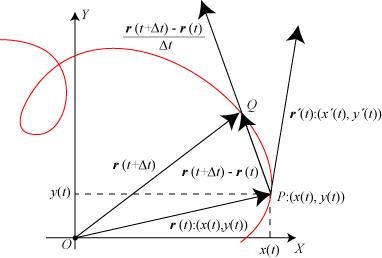
Når man skal arbejde teoretisk med vektorfunktioner, undgår man i reglen at arbejde i et koordinatsystem. Man klarer sig - som ovenfor - med et begyndelsespunkt O. Men når man skal arbejde med en konkret vektorfunktion, arbejder man i reglen i et koordinatsystem. Det lægges med begyndelsespunkt i O, sådan som det er vist på figuren her. Vektoren r(t) har så to (i rummet tre) koordinater, som selv er funktioner af t. Her beskriver vi kun forholdene i planen. Her betegnes koordinatfunktionerne x(t) og y(t), og man skriver som sædvanlig r(t): (x(t),y(t)). Koordinaterne til r´(t) bliver så x´(t) og y´(t), altså r´(t):(x´(t),y´(t)). Man kalder (x,y) = (x(t),y(t)),    a < t < b, for en parameterfremstilling for den røde kurve. Kurvens tangent i punktet P er bestemt af vektoren (x´(t),y´(t)).

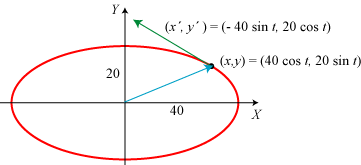Vi tager et lille eksempel: Parameterfremstillingen (x,y) = (40 cos t, 20 sin t),    0 ≤ t < 2π, fremstiller en ellipse med halvakserne a = 40 (mm) og b = 20. Tangenten i det punkt, der svarer til parameterværdien t, er da bestemt af vektoren (x´,y´) = (− 40 sin t, 20 cos t), der er tegnet grøn på figuren. Figuren viser situationen for t = 40°, hvor (x,y) = (30,64 , 12,9) og (x´,y´) = (- 25,7 , 15,3).. Se hvor let det er at finde tangenter, når man har lært at differentiere.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.