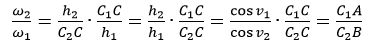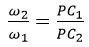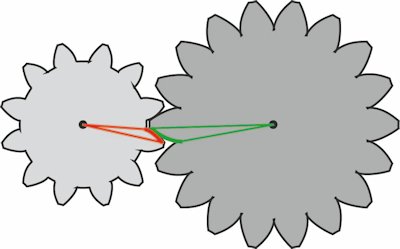
En hovedsætning om jævne tandhjul

Omkring 1675 foreslog Ole Rømer en bestemt form for tænderne i et tandhjul. Den form beskrives udførligt her på siden under Rømer i 1675. Formålet med Rømers tandhjul var at sikre, at når det ene af to tandhjul i indgreb bevæger sig med konstant vinkelhastighed, da vil det andet også bevæge sig med konstant vinkelhastighed. Tandhjul med denne egenskab kalder vi her "jævne". Med jævne tandhjul undgår altså de små variationer af vinkelhastigheden ved passage af hver enkelt tand, der vil finde sted, hvis man bruger tilfældige tandformer. Man kan også sige, at to tandhjul er jævne, når forholdet mellem deres vinkelhastigheder er konstant, mens tandhjulene drejer sig.

Der er en hovedsætning om jævne tandhjul. Jeg ved ikke hvornår sætningen blev fundet, og jeg ved heller ikke hvem der fandt den. D´Alembert kendte sætningen, da han skrev om tandhjul i Encyclopedien. Se under 1748 D´Alembert.

Her kommer sætningen med et bevis.

På figuren til højre viser vi to tandhjul i indgreb. Når man skal undersøge om tandhjulene er jævne er det nok at man undersøger ét forløb, hvor to nabotænder rører ved hinanden. Så på figuren vil vi undersøge det korte tidsinterval, hvor den røde tandside rører den grønne. Den undersøgelse er overordentlig kompliceret. Det fremgår tydeligt af figuren nedenfor, hvor vi viser en forstørret udgave af de to farvede kurver og linjestykkerne fra kurvernes endepunkter ind til tandhjulenes centre.

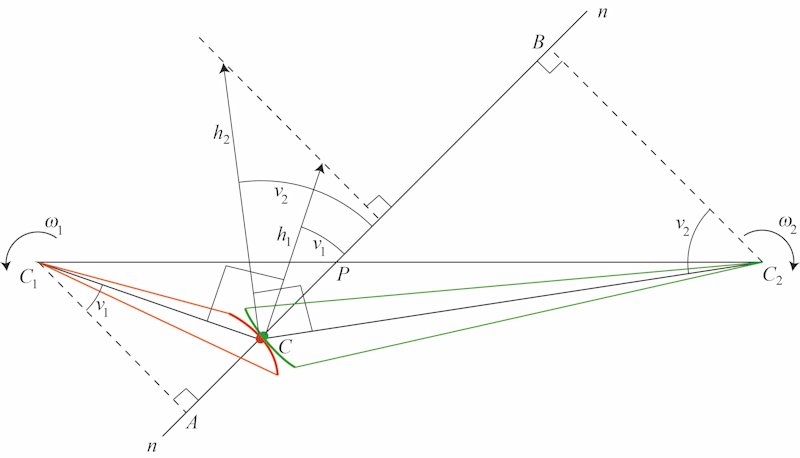
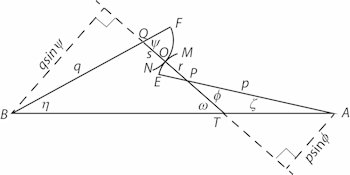
Vi starter med at beskrive, hvad det er, vi viser på figuren: Først og fremmest er den et øjebliksbillede fra den kortvarige bevægelse vi nævnte ovenfor. Den vandrette linje, som ligger stille, forbinder tandhjulenes centre C₁ og C₂ som også ligger stille. Det røde drejer sig om C₁ med vinkelhastighed ω₁, og det grønne drejer sig om C₂ med vinkelhastighed ω₂. Vinklerne måles i radianer. Alt andet på figuren bevæger sig også - med en lille undtagelse, som vi kommer tilbage til. Det øjeblikkelige røringspunkt C bevæger sig på begge kurver, men i vores overvejelser får vi brug for et rødt punkt C og et grønt punkt C. C er et punkt, der ligger fast på den røde kurve og som bevæger sig sammen med den, og C er et punkt, der ligger fast på den grønne kurve og som bevæger sig sammen med den. I det betragtede øjeblik falder C og C sammen med det øjeblikkelige røringspunkt C.

På figuren har den røde og den grønne kurve en fælles tangent i punktet C. Tangenten vises ikke på figuren, men det gør dens normal n i punktet C. Den normal spiller en vigtig rolle i det følgende. n bevæger sig for det gør de to kurver. P er skæringspunktet mellem centerlinjen og n. Linjestykkerne C₁A og C₂B er normaler til n fra de to centre.

h₁ er hastighedsvektoren for det røde C og h₂ er hastighedsvektoren for det grønne C. Disse to hastighedsvektorer må som vist på figuren have samme projektion på n. Ellers ville de to kurver ikke berøre hinanden et øjeblik senere. Da C og C deltager i rotationen af hver sit tandhjul er h₁ vinkelret på C₁C og h₂ er vinkelret på C₂C. Af samme grund er længderne af hastighedsvektorerne

h₁ = ω₁·C₁C    og    h₂ = ω₂·C₂C.

Som nævnt har h₁ og h₂ samme projektion på n. Derfor er

h₁ cos v₁ = h₂ cos v₂

Vi kan nu udregne forholdet mellem de to vinkelhastigheder:

Da trekanterne A C₁P og B C₂P er ensvinklede fås heraf, at

Af denne formel aflæses følgende 2 hovedresultater:

1. Hvis forholdet mellem vinkelhastighederne er konstant under bevægelsen vil P ligge fast under bevægelsen som det punkt, der deler centerlinjen i stykker der forholder sig som vinkelhastighederne. Linjen n går hele tiden gennem P.

2. Hvis man omvendt iagttager, at der er et punkt Q på centerlinjen, som alle normaler går igennem, må specielt må n på iagttagelsestidspunktet gå gennem Q. Q er derfor punktet P på figuren ovenfor, og af formlen aflæser man så at forholdet mellem vinkelhastighederne er konstant.

I den supplerende artikel om tandhjul er Euler tæt på at bevise i hvert fald det første hovedresultat. Vi viser herunder med kommentarer, hvad Euler skriver om hovedsætningen.

Lad Π være det tryk, med hvilket tænderne i punktet O påvirker hinanden. (Euler tænker på trykkets komposant på linjen QT) I begge retninger ligger trykket på linjen QT. Så vil momentet på hjulet A være M = Πp sinΦ, og på hjulet B vil det være Πq sinΨ. Vi antager nu, at det moment, der får hjulet med centrum A til at dreje om sit centrum er sådan, at vinklen ζ forøges og at momentet M er konstant. Hvis det andet hjul også drejer sig med konstant vinkelhastighed må det være påvirket af et konstant moment. Da vil det moment, som det andet hjul drejes omkring B med være M1  =  ΠqsinΨ  = og dette vil ske på den måde, at vinklen η forøges. Brøken skal altså have en konstant værdi. Men så må forholdet mellem linjestykkerne AT og BT også være konstant nemlig AT:BT = psinφ:qsinψ . Ud fra dette vil punktet T være fast, sådan at AT´s forhold til BT er lig med forholdet mellem de momenter, der drejer A rundt og B rundt.

I dag vil man betragte drejningsmomenter, som noget der skal afgøres i fysisk eller teknisk sammenhæng. At finde en form på tænderne i to tandhjul, der sikrer at begge tandhjul drejer sig med konstante vinkelhastigheder er ren matematik. Når tandhjulene er konstruerede kan de dreje sig uden ydre påvirkning. Det kommer som en overraskelse at Euler inddrager drejningsmoment i sine overvejelser. Det resultat, han kommer frem til, nemlig at den nævnte brøk er konstant, er korrekt. Euler nævner ikke direkte, at dette forhold er lig med forholdet mellem de vinkelhastigheder, som tandhjulene drejer sig med. Dette er den ene halvdel af en central sætning om tandhjul, som vi her på siden beviser under 1742 En sætning om tandhjul, der er link for oven. Jeg ved ikke hvem der først fandt denne sætning.

Nedenfor viser jeg et eksempel på to jævne tandhjul. De er af den type, som Euler fandt.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.