|
Forside
Søgning
Liste |  |
Centrifugalkraft
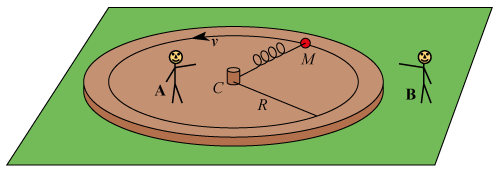
På en græsplæne er der en brun karrusel uden rækværk. Den drejer sig om centrum C, så punkterne på cirklen med radius R har hastigheden v. Fysiker A står på karrusellen og taler med fysiker B, der står på græsplænen:
A: Jeg begriber det ikke. Jeg har en rød kugle med masse M. Da jeg for lidt siden
lagde kuglen ned på karrusellen begyndte den af sig
selv at trille til siden. Efter mange forsøg fik jeg den i ro ved hjælp af en fjeder, der via to snore forbinder
kuglen til cylinderen C. Fjederen hiver ret kraftigt i kuglen.
B: Hvad er problemet??
A: Hvorfor hiver fjederen ikke kuglen ind mod C, der er jo ikke noget, der hiver den anden vej?
B: Har du overhovedet lagt mærke til, at karrusellen drejer rundt?
A: Ja, men Newtons love gælder vel også på karruseller!
B: Nej, det gør de faktisk ikke.
A: Det kunne han godt have sagt.
B: Det gjorde han også, han sagde nemlig, at tingene skulle beskrives i et koordinatsystem, der ligger
fast i forhold til stjernehimlen.
A: Hvad gør man så, hvis man står på karrusellen, og skal regne noget ud, baseret på iagttagelser?
B: Set fra mit synspunkt er der ikke noget problem.
Ifølge 1659 Huygens og Newtons 2. lov er den kraft, som fjederen påvirker M med
M·v2/R, så det er netop den kraft, der kan holde kuglen på
plads i sin cirkelbevægelse. På karrusellen mangler du en udadrettet kraft af samme størrelse. Så hvis du tilføjer den
så kan du godt foretage dine observationer og beregninger på karrusellen, uden på anden måde at tage hensyn til at den
roterer. Det er denne tilføjede kraft, der kaldes centrifugalkraften. Paradokset forsvinder så fordi fjederkraften
ophæves af centrifugalkraften og kuglen derfor godt kan ligge stille på karussellen, sådan som du har iagttaget.
A: Det kan jeg godt se, men er det ikke en mystisk kraft, der ikke kommer nogen steder fra?
B: Jo, og derfor kalder man den også en fiktiv kraft. Men du har tit mærket den. Når f.eks. bilen drejer til venstre,
så mærker du tydeligt en kraft, der presser dig til højre.
Vi tager et eksempel:
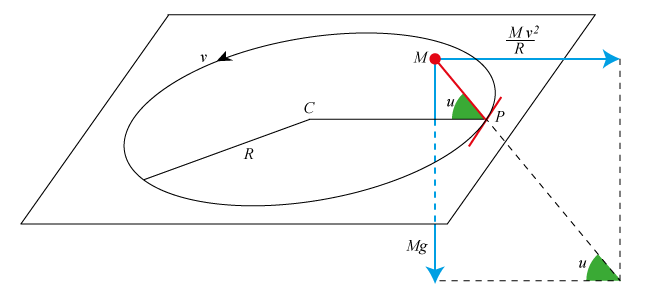
Vi vil undersøge ligevægtsbetingelsen for den røde model på billedet. Vi fortæller senere, hvad det er en model af. Modellen består af to korte vægtløse stænger og en punktformet masse M. Stængerne er vinkelrette på hinanden, og de mødes i punktet P. Den ene stang er hele tiden tangent til banecirklen, og den anden stritter skråt op i luften. Den danner vinklen u med vandret og den bærer foroven massen M. Punktet P gennemløber banecirklen med hastigheden v. M gennemløber en vandret cirkel et stykke oppe, og da den skrå stang er kort i forhold til cirklens radius regner vi med, at de to cirkler er lige store og at de gennemløbes lige hurtigt. På figuren har vi vist to kræfter, som M er påvirket af, nemlig tyngdekraften Mg og centrifugalkraften M·v2/R. Kræfterne er vektorer, der er tegnet blåt på figuren.
Hvis u er større end 90° vil kræfterne få M til at falde ned til højre i den vandrette plan. Hvis u er i nærheden af 0° vinder tyngdekraften og M falder ned til venstre i den vandrette plan. Der må derfor være en værdi af u for hvilken M balancerer på enden af sin stang. Denne situation opstår, når summen af de to kraftvektorer går i forlængelse af MP, sådan som det er vist på figuren. Da de to grønne vinkler er lige store, fås af figuren, at
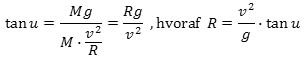
Hvis R vælges sådan balancerer massen M på toppen af den skrå stang.
 |
Den røde figur kunne være model af en skøjteløber, |
Hvis man f.eks sætter v = 4 m/sek (= 14 km/T), g = 10 m/sek2 og R = 10 m får man tan u = 100/16 = 6,25, hvoraf u = 80°, og det virker rimeligt.
| Opgave 19 - eller måske er det snarere et projekt, som passende kunne udføres af en lille gruppe gymnasieelever. Jeg kunne godt tænke mig et billede af en cyklist i stedet for skøjteløberen ovenfor. Foruden billedet skal der være måling af baneradius, hastighed, og vinkel alle med angivne usikkerheder. Kommenter også hvor godt det passer med formlen. Hvis rapporten er god, kommer I også på forsiden i en periode. |
Ideen til disse eksempler fik jeg fra følgende spørgsmål fra en bruger af hjemmesiden: En bil, der har dæk, der ikke kan skride ud, kører 72 km/T = 20 m/sek. Hvor skarpt et hjørne kan den dreje omkring uden at vælte? Den røde model kunne være en model af bilen. Den vandrette stang er den nederste højre side af bilen og M er bilens masse, samlet i dens tyngdepunkt. Så er den situation, som vi har bestemt ovenfor grænsen mellem en bil der vælter ud til højre og en bil, der kører videre langs cirklen. Vinklen u er summen af vippevinklen og den vinkel, som PM danner med vandret, når bilen kører almindeligt
Hvis vi i formlen sætter v = 20 m/sek, g = 10 m/sek2 og for eksempel u = 20° får man, at R = 14 meter.
Af formlen ses, at hvis hastigheden v fordobles, så øges den kritiske R-værdi til det 4-dobbelte. Vinklen u skal være lille, hvis man vil kunne køre meget krumt. Det opnås med en bred bil med et lavt tyngdepunkt. Hører jeg nogen mumle Formel 1?
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |