Forside Søgning Liste

Tyngdefeltet omkring en kugle.

Newton lagde stor vægt på, at det var et bevis for holdbarheden af hans gravitationslov, at det er den samme lovmæssighed, der bestemmer Månens bevægelse om Jorden, som den, der bestemmer faldet af en genstand her på jordoverfladen. Newton kunne først føre dette bevis, når han havde fundet ud af, hvordan Jordens tyngdefelt varierer tæt ved Jordens overflade. Problemet er, at man så skal tage i betragtning, at Jorden mildt sagt ikke er en punktformet massepartikel, men har en betydelig udstrækning.

Newton fandt tyngdefeltet omkring Jorden ved først at opfatte Jorden som sammensat af tynde homogene kugleskaller med centrer fælles med Jorden. Kugleskal skriver vi. Det betyder, at den er hul indeni. Newton starter med at bestemme det tyngdefelt, som sådan en kugleskal danner omkring sig.

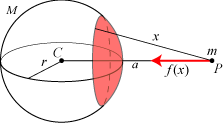På figuren viser vi én af disse tynde kugleskaller. Kugleskallen har radius r, masse M og centrum i Jordens centrum C. Til højre på figuren er der en partikel P. Den har masse m, og dens afstand fra C er a. Newton starter med at bestemme den tyngdekraft F, som kugleskallen påvirker P med. Vi løser opgaven ved hjælp af integration. Vi starter med at betragte den røde kuglekalot, der er vist på figuren. Alle punkter på dens begrænsningscirkel har afstanden x fra P. Kalotten skal opfattes som en del af kugleskallen. Den røde kraft ud fra P er den tyngdekraft, som kalotten påvirker P med. Det er en funktion f (x) af x, der er defineret i intervallet a-r ≤ x ≤ a+r. Specielt er f (a-r) = 0 og f (a+r) = F, dvs. den søgte tyngdekraft fra hele kugleskallen.

f (x) betyder den tyngdekraft, som den røde kuglekalot påvirker partiklen P med.

Vi vil nu bestemme funktionen y = f (x) ved først at finde dens differentialkvotient f ´(x). Vi benytter definitionen af differentialkvotient og starter derfor med at give x en lille tilvækst Δx. Herved bliver kuglekalotten forøget med en ring R, som er tegnet blå på figuren. Ringens masse betegnes ΔM. Tilvæksten Δx på x bevirker en forøgelse Δy af tyngdekraften på P. Denne forøgelse skyldes ringen R. Så nu går vi over til at beregne den tyngdekraft, som R påvirker P med.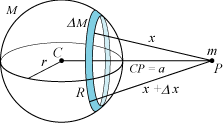

Figuren nedenfor viser en (lodret) snitplan, der indeholder linien CP. Man set to tværsnit i ringen R. De er vist med blåt på figuren. Ved hjælp af et stort antal planer gennem CP skærer vi R i et lige antal kongruente småstykker. De to røde kræfter på figuren er de tyngdekræfter, som de to blå småstykker, der ses på figuren, påvirker P med. Nu kan man af parallellogrammet ude til højre se, at hvert lille blåt ringstykke bidrager til tyngdekraften på P med den røde krafts blå projektion på PC. Adderes disse bidrag hele ringen rundt, får vi af gravitationsformlen, at ringen R påvirker P med en tyngdekraft rettet mod C af størrelsen

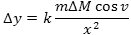
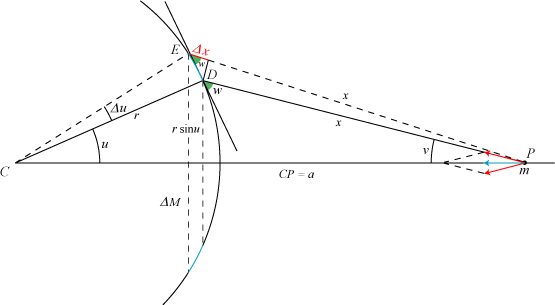
Vi skal nu erstatte de variable ΔM og v med udtryk i x og Δx. Vi starter med at udtrykke ΔM ved M og u. Ringens omkreds er 2πrsinu, og dens bredde er rΔu. Ringens overfladeareal ude på kuglen er produktet af disse to størrelser, altså 2πr²Δusinu. Den lille fejl, som vi begik her, forsvinder, når vi senere lader Δx→0. Da hele kuglens overflade er 4πr², får vi, at

så

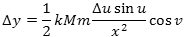
Vi vil nu udnytte, at de to grønne vinkler w er lige store. Herved begår vi en lille fejl. Den forsvinder, når vi senere lader Δx→0. w kan findes ved at man anvender sinusrelationen på trekant PCD:

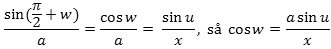
Af den lille trekant for oven fås nu, at

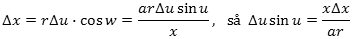
Her har vi igen begået en lille fejl, idet vi har sat buen ED lig et liniestykke. Igen forsvinder fejlens betydning, når vi senere lader Δx→0.

Indsættes dette i udtrykket for Δy fås, at

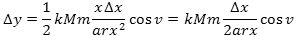
Her kan cosv udtrykkes ved x, ved at man bruger cosinusrelationen på trekant PCD:

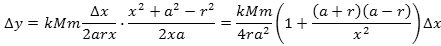
Og så er vi efter en del besvær nået frem til en formel, hvor udtrykket for Δy kun indeholder én variabel, nemlig x. Beviset ændres lidt, hvis D ligger på den venstre halvdel af kugleskallen, men resultatet er det samme. Af formlen følger, at

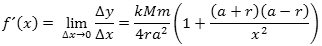
Det ser lidt mærkeligt ud, at forholdet Δy/Δx tilsyneladende ikke afhænger af Δx. Det er også kun tilsyneladende, det skyldes de små fejl, som vi fornuftigvis har begået. Vi kan nu bestemme funktionen f (x) ved integration. Resultatet er, at

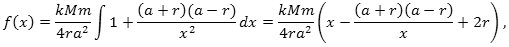
hvor integrationskonstanten 2r er bestemt, så f (a-r) = 0. Den samlede tyngdekraft fra hele kugleskallen på P bliver derfor

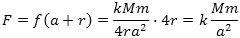
F har altså samme værdi som den ville have, hvis hele kugleskallens masse var samlet i punktet C.

Så mangler vi bare, at lægge kræfterne fra alle kugleskallerne sammen, så vi får den samlede tyngdekraft F, som den massive kugle med masse M påvirker P med. Det er nu en let sag. Vi kalder masserne af kugleskallerne M₁, M₂, M₃, ... og får så ifølge det fundne kugleskalsresultat, at

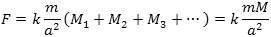
Det gælder altså også for en massiv kugle, af tyngdefeltet omkring den ikke ændres ved, at man samler al dens masse i centrum.

Resultatet er overraskende simpelt, men beviset ovenfor giver ingen anskuelig forståelse af, hvorfor det forholder sig, som det gør. Den grundlæggende struktur i beviset skyldes Newton, men den lange række formler og integrationen findes ikke hos Newton. Den er hos ham erstattet af en vanskelig tekst i klassisk græsk stil. Muligvis har Newton fundet resultatet, omtrent som vi har gjort her, men i publikationen har han altså valgt en anden fremgangsmåde.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.