Forside Søgning Liste

Udgangspunktet for Jordanus arbejder er et aksiom, "Jordanus Aksiom". Det lyder således:

Hvis noget kan løfte en vægt til en bestemt højde, så kan det samme løfte en k gange så stor vægt til en k gange så lille højde

Vi vil gennemgå tre af de anvendelser, som Jordanus gjorde af aksiomet. Det drejer sig om ligevægt på et skråplan og om to versioner af vægtstangsreglen.

1. Ligevægt på et skråplan

Figuren nedenfor viser et skråplan, hvor der er ligevægt mellem to vægte M og m. Vi tænker os, at vægten M flyttes nedad skråplanet langs den punkterede linie, således at den falder højden h. Så løftes vægten m op langs sin punkterede linie og hæves højden H. Det følger da af Jordanus aksiom, at hvis M er k gange større end m, så vil h være k gange mindre end H. Derfor er

Mh = mH

I dag vil vi begrunde denne ligning ved at sige, at mH er m´s tilvækst i potentiel energi, mens Mh er M´s tab af potentiel energi. Da energien er konstant, må Jordanus aksiom derfor være opfyldt. Jordanus kendte ikke begreberne arbejde og energi, men det er tydeligt, at han fornemmede noget i denne retning, da han formulerede sit aksiom.

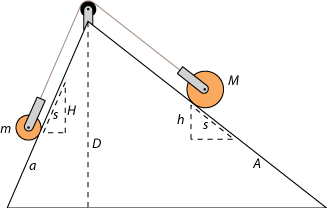
Vi går nu over til at udlede Jordanus ligevægtsbetingelse. I betingelsen indgår længderne A og a af skråplanets to sider.

Af ensvinklede trekanter fås, at

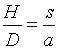og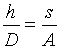

Ved division fås, at

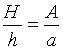
Sammenholdes dette med Jordanus aksiom fås endelig, at

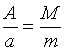
hvilket er Jordanus ligevægtsbetingelse. Set ud fra tidens forudsætninger er det en meget tilfredsstillende betingelse. Betingelsen er korrekt, og det er ikke svært at vise, at den er ækvivalent med det resultat man får ved at bruge reglen om kræfternes parallellogram. Det er interessant, at selv om det drejer sig om at finde en ligevægtsbetingelse, så betragtes undervejs en tænkt bevægelse, en "virtuel bevægelse". Såvidt vi ved, var Jordanus den første, der brugte virtuelle bevægelser i statikken. Virtuelle bevægelser fandt senere en vigtig plads i mekanikken.- Stevin fandt et meget elegant argument for skråplansreglen.

2. Jordanus argument for vægtstangsreglen

Jordanus fandt ud fra sit aksiom et meget originalt bevis for vægtstangsreglen. Jordanus havde ikke kendskab til hverken Herons eller Archimedes arbejder. Vi betragter en vandret vægtstang, som kan dreje sig om et punkt c. Vi tænker os, at der i punkterne a og b er anbragt to vægte, som vi også betegner a og b. Vi vælger afstandene ca og cb så deres forhold er b/a. Og nu følger vi så Jordanus formulering:

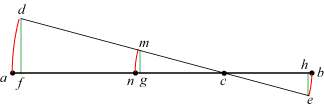
Argumentet er meget originalt. Det fortjener respekt. Igen benyttes en virtuel bevægelse. Det er ikke svært at efterprøve vægtstangsreglen ved praktiske forsøg. Når Jordanus ikke desto mindre foretrækker en aksiomatisk fremstilling frem for eksperimenter, skyldes det formodentlig den succes, som Oldtidens grækere havde med en aksiomatisk opbygget matematik og vel også grækernes uvilje mod eksperimenter.

2. Den knækkede vægtstang

Nej, det er ikke en vittighed, Jordanus undersøgte faktisk også ligevægtsbetingelsen for en vægtstang, der ikke er retlinet. Vi antager, at vægtstangen selv ikke vejer noget, og betragter den type vægtstang, der er vist med brunt på figuren nedenfor. Den består af to retlinede stænger, der har forskellig længde, og som er stift forbundet med hinanden i et punkt O, som den samlede stang frit kan dreje sig om. I den frie ende af hver af de to stænger er der anbragt en sort vægt, samme vægt begge steder. Vi ønsker at finde ligevægtsstillingen, dvs den stilling, som stangen falder til ro i, hvis den bliver overladt til sig selv. Vi kan roligt antage, at den lange stang er til højre, og den korte til venstre.

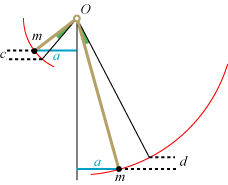Jordanus antager nu, at de to blå liniestykker har samme længde. Liniestykkerne går fra vægtene og vinkelret ind til den lodrette linie gennem ophængningspunktet. Og det skal nu bevises, at der er ligevægt. Beviset benytter igen en virtuel bevægelse, idet vi antager, at hvis vi slipper vægtstangen i den tegnede stilling, så vil den af sig selv dreje sig f.eks. mod uret. På figuren har vi tegnet situationen, når vægtstangen har drejet sig en ganske lille grøn vinkel. De sorte linier viser vægtstangen i den nye beliggenhed. Vægten til venstre har flyttet sig stykket c nedad, mens vægten til højre har flyttet sig stykket d opad. Imidlertid er d > c. Men det er i modstrid med Jordanus aksiom, der i tilfælde af lige store vægte siger, at hvis den ene vægt går stykket c nedad, da vil den anden vægt gå samme stykke opad. Vores antagelse var altså forkert, og den oprindelige stilling var altså ligevægtsstillingen.

At d > c nævner Jordanus uden argumentation. Jeg har ikke kunnet finde noget simpelt argument for, at det er rigtigt. Du kan finde et bevis her.

Selv om Jordanus bevis altså er mangelfuldt, så er resultatet rigtigt og vigtigt. Det introducerer begrebet moment som vægt multipliceret med arm, et vigtigt fremskridt i mekanikkens historie. Heron kendte også resultatet, men det vidste Jordanus ikke. Jordanus er også tæt på begrebet potentiel energi.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.