Om manglen i beviset.
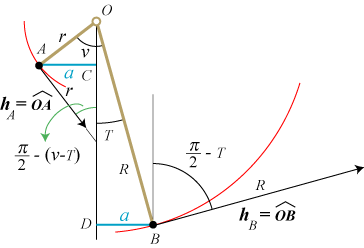
Vi skal vise, at d > c. På figuren viser vi igen den knækkede vægtstang. Vi tænker os, at stangen drejer sig om punktet O med vinkelhastighed 1. Endepunkterne A og B bevæger sig derfor med fart r og R i retning af tangenten til banecirklerne. C og D betegner projektionerne af A og B på den lodrette linie gennem O. T er det tidspunkt, hvor a=AC=BD, og figuren viser situationen til tidspunktet T. Det gælder altså, at
a = r sin (v−T) = R sin T
Det vi skal vise er, at i et kort tidsinterval, der starter med tidspunktet T, bevæger C sig mindre nedad, end D bevæger sig opad.
Hastighedsvektorerne hA og hB for punkterne A og B er tværvektorer til OA og OB, sådan som det er vist på figuren. De hastigheder hC og hD, som C og D bevæger sig med til tidspunktet T, findes ved projektion af hastighedsvektorerne hA og hB på den lodrette linie:
hC = r cos (½ π-( v−T)) = r sin (v−T) og hD = R cos (½ π - T) = R sin T
Øv, til tidspunktet T bevæger de to punkter C og D sig altså mod hinanden med samme hastighed h = hC = hD, så vi fik ikke det ønskede at vide. Men det er da et smukt resultat, at i det øjeblik de to blå liniestykker er lige lange, bevæger C og D sig med samme fart. Ikke desto mindre kan man bruge resultatet til at komme videre med!:
Vi starter med at minde om, at når et punkt P udfører en harmonisk svingning med centrum O, så vokser punktets hastighed, når det bevæger sig ind mod O, mens punktets hastighed aftager, når det bevæger sig væk fra O.
På figuren udfører både C og D harmoniske svingninger omkring centret O. Amplituderne er r og R. Lige efter tidspunktet T vil C bevæge sig væk fra O, og derfor vil C få hastighed < h. D derimod bevæger sig ind mod centret og får derfor hastighed > h. Efter passagen af tidspunktet T har D derfor mere fart på end C, og derfor er d > c.
Jordanus kendte godt sinusfunktionen, men vi ved ikke, om han havde mulighed for at finde på et
argument som ovenstående.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |