Forside Søgning Liste

Bestemt integration blev udført allerede i græsk Oldtid bl. a. af Eudoxos og Archimedes. Senere udførte Oresme, Stevin og mange andre integrationer. Men fælles for alle de integrationer, der blev udført før 1670, var, at integrationsprocessen i hvert enkelt tilfælde blev tilpasset det aktuelle problem. Det, som Newton og Leibniz gjorde omkring 1670, var - på hver sin måde - at udforme en abstrakt integrationsproces, der så, uden store intellektuelle vanskeligheder, kunne anvendes til løsning af et utal af problemer. Den fremstillingsform, der bruges i dag, skyldes Leibniz. Mens begrebet differentialkvotient er udsprunget af ønsket om at kunne bestemme kurvetangenter, var arealbestemmelse et vigtigt incitament til indførelse af integralbegrebet. At disse to problemstillinger er nært beslægtede, kom som en overraskelse for det sene 1600-tals matematikere

1. Ubestemte integraler

Begrebet ubestemt integral bygger på funktionsbegrebet og på begrebet differentiation. En funktion y = f(x), a ≤ x ≤ b er et regneudtryk eller en anden udregningsforskrift med den egenskab, at der for ethvert x i intervallet fra a til b kan udregnes én og kun én værdi y = f(x). Eksempler på funktioner er

En sådan funktion y = f (x) har en differentialkvotient y´ = f´(x), og man kalder så y for integralet (eller det ubestemte integral) af y´ og skriver ∫ y´dx = y. Her kommer nogle eksempler:

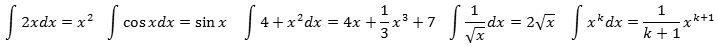
Det mærkelige integraltegn og det tilhørende symbol dx er indført af Leibniz. Oprindelsen til dem forklares nedenfor i afsnittet om bestemte integraler.

Du kan kontrollere, at integralerne er rigtigt regnet ud ved at differentiere resultatet; så skal du få det, der står under integraltegnet. Læg mærke til, at 7-tallet i det tredje eksempel godt kunne fjernes, det forsvinder jo ved differentiationen. Når man har udført en integration, kan man altså altid lægge en konstant til. I matematikken bevises det, at bortset fra en sådan konstant er resultatet af en integration altid entydigt bestemt. Et ubestemt integral af en funktion kaldes også en stamfunktion til funktionen.

For integration gælder der en lang række regneregler. Her følger nogle af de vigtigste:

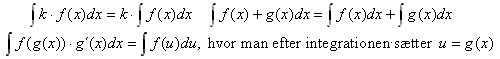
Vi slutter dette afsnit med at vise, at man ved integration let kan finde Galileis formel for det skrå kast.

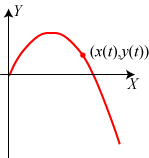Vi går ud fra, at her på jordoverfladen får en partikel af tyngdekraften en lodret nedadrettet acceleration af størrelsen g = 9,8 m/sek². Figuren viser en lodret plan, hvor en partikel til tidspunktet t = 0 fra koordinatsystemets begyndelsespunkt kastes skråt op i luften og beskriver den røde banekurve. Til tidspunktet t har partiklen koordinaterne (x(t), y(t)). Ifølge definitionen af acceleration bliver accelerationen derfor (x´´(t), y´´(t)) = (0, - g). Ved integration fås heraf, at hastigheden til tidspunktet t er (x´(t), y´(t)) = (a, - gt + b), hvor a og b er integrationskonstanter. Deres betydning er, at (a, b) er den hastighed, som partiklen starter med. Ved yderligere en integration fås herefter, at (x(t), y(t)) = (at + c, - ½gt² + bt + d), hvor c og d er to nye integrationskonstanter. De er imidlertid begge 0, da bevægelsen starter i punktet (0,0). Resultatet er altså, at (x(t), y(t)) = (at, - ½gt² + bt) og dette er parameterfremstillingen for en parabel, Galileis kasteparabel.

2. Areal under et stykke parabel

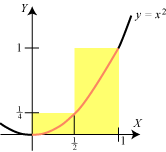
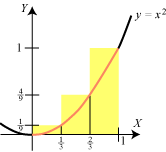
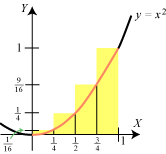
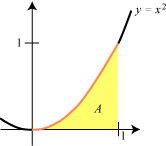Vi vil prøve at bestemme arealet A af det gule område på figuren. Det ligger i intervallet fra 0 til 1 mellem parablen y = x2 og X-aksen. Det er ikke en let opgave. Den sædvanlige måde med at dele i trekanter og lægge deres arealer sammen duer ikke på grund af den krumme parabel. Det er let nok at finde en tilnærmet værdi af arealet. Man kan bare vælge en retlinet figur, som nogenlunde falder sammen med det gule område. Nedenfor viser vi et forsøg i denne retning, hvor den retlinede figur består af rektangler med bredden 1/n for n = 1, 2, 3 og 4. Det ser ud til, at arealet er noget i retning af 0,4, men nogen nøjagtig besked fås ikke af denne metode.

Areal af det gule område	1,000	5/8 = 0,625	14/27 = 0,519	30/64 = 0,469

Det næste, vi så vil prøve, er at regne ud, hvad tilnærmelsen bliver, hvis man deler i n lige store dele, der så hver får bredden 1/n. Figuren viser det p-te gule rektangel, og man ser, at dets areal er p2/n3. Hvis vi så lader p antage værdierne 1, 2, 3, ... , n og lægger arealerne sammen, får vi, at den samlede tilnærmelse An til arealet bliver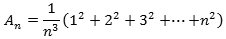 og jeg kan altså ikke finde ud af, hvad denne sum nærmer sig til, når n bliver meget stor. For n = 10 bliver summen 0,385, og hvad ligger det i nærheden af? Det var en metode som denne, som Eudoxos, Archimedes, Oresme og Stevin benyttede, men hver gang kom de til et nyt svært problem som ovenstående. Archimedes løste faktisk vores problem, se her.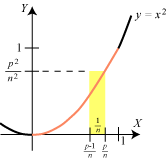

For at komme videre med arealbestemmelsen må vi præsentere læseren for den største opdagelse i matematikkens historie. Intet mindre!

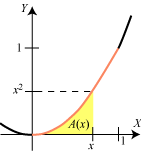Den grundlæggende ide er følgende: Vi vælger et x mellem 0 og 1 og lader A(x) betegne arealet af det område, der er vist på figuren. Og så vil vi bestemme funktionen A(x). (Her vil den interesserede læser sukke dybt og tænke: Det kan da umuligt være lettere end at finde det oprindelige areal A!) Jo, for pointen er, at nu vil vi ikke finde arealet ved tilnærmelse med en retlinet figur, nu vil vi finde A(x) ved at finde dens differentialkvotient A´(x). Da vi nu befinder os i slutningen af 1600-tallet er der det problem, at vi først skal have opfundet differentialregningen. Det tænker vi os nu gjort, og for at finde A´(x) bruger vi definitionen af en differentialkvotient.

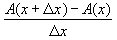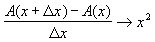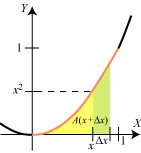Vi giver x en lille tilvækst Δx. Så får A(x) en tilvækst, der er det grønne areal på figuren. Tælleren i brøken er altså det grønne areal på figuren. Når man dividerer arealet af et højt, smalt rektangel med længden af den korte side, får man højden. Og jo mindre Δx er, jo nærmere er det grønne område ved at være et højt smalt rektangel. Når Δx → 0 vil derfor

Der gælder altså A´(x) = x², så vi har fundet den søgte funktions differentialkvotient. Så finder man funktionen selv ved integration:

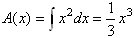
Her har vi, da A(0) = 0, set bort fra integrationskonstanten. Slutresultatet er altså, at A = A(1) = 1/3.

Ved denne simple integration har vi altså undgået en meget svær undersøgelse af summen af de n første kvadrattal, og faktisk har vi som biresultat og af en sær vej fået vist, at

    

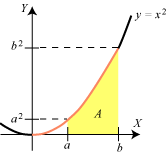
For at få det principielle tydeligt frem ændrer vi nu opgaven en smule, idet vi ønsker at bestemme det gule areal A på figuren til venstre. Det gør vi ligesom ovenfor ved først at bestemme det gule areal A(x) på figuren til højre. Nøjagtigt som før kan man bevise, at differentialkvotienten A´(x) = x². A(x) selv finder vi så ved integration:

Her kan vi ikke se bort fra konstanten k. Men vi kan benytte, at A(a) = 0. Derfor må k = −1/3 a³, så resultatet er, at

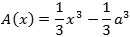
Arealet A fås heraf, ved at man sætter x = b:

Symbolet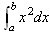

kaldes det bestemte integral fra a til b af funktionen y = x2. Det defineres således:

Først findes en stamfunktion F(x) til y = x².

Så sætter man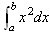

= F(b) − F(a).

Det, som vi har vist ovenfor, er så, at A =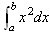

3. En generel arealformel og det bestemte integral

Den behandling, som vi ovenfor har givet funktionen y = x², lader sig uden videre gentage anvendt på en vilkårlig funktion y = f(x). Det gør vi nu:

    

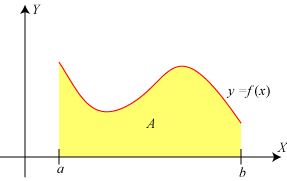
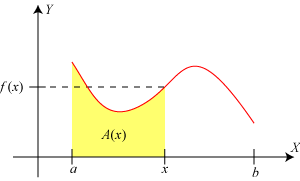
Vi vil bestemme det areal A, som er vist på figuren til venstre. Det gør vi ved først at finde arealet A(x) på figuren til højre. Nøjagtig som ovenfor indser vi, at A´(x) = f(x). Lad F(x) være en stamfunktion til f(x). Så må der findes en konstant k, så A(x) = F(x) + k. Da A(a) = 0, må k = −F(a). Derfor er A(x) = F(x) − F(a), og dermed har vi fundet det søgte areal

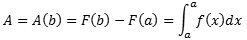
hvor det sidste lighedstegn er definitionen af det bestemte integral. Vi definerer altså det bestemte integral fra a til b af f (x) som differensen F(b) − F(a), hvor F(x) er en stamfunktion til f(x). Af denne definition følger umiddelbart indskudsreglen

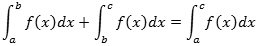
Med disse få bemærkninger har vi altså fundet en formel til at bestemme arealet af et område, der i et interval fra a til b ligger mellem X-aksen og kurven y = f (x). Betingelsen for, at man kan bruge formlen, er, at man kan finde en stamfunktion til f(x). Hvis man regner arealer, der ligger under X-aksen, for negative, gælder formlen også for funktioner, der antager negative værdier.

4. Differential- og integralregningens hovedsætning

Integration kan benyttes til meget andet end arealbestemmelse. I mange tilfælde hænger dette sammen med, at bestemte integraler kan bruges til beregning af en vigtig klasse af summer. Det hænger sådan sammen:

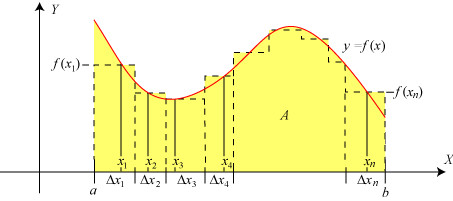
På figuren har vi opdelt stykket fra a til b i n små stykker med længderne Δx₁, Δx₂, Δx₃, ... Δx_n. I hvert interval har vi valgt en x - værdi. De hedder x₁, x₂, x₃ , ... , x_n. Så er det samlede areal af de viste punkterede rektangler

Denne sum kaldes en middelsum for f(x) i intervallet fra a til b. Hvis vi nu lader n vokse ud over alle grænser og lader alle Δ_i - erne aftage ubegrænset mod 0, så vil

f (x1)·Δx1+ f (x2)·Δx2+ f (x3)·Δx3+ ... + f (xn)·Δxn →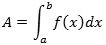

Under grænseovergangen vil det samlede areal af de små "fejltrekanter" nemlig gå mod nul. Man kan f.eks. vælge n så stor og Δ-erne så små, at fejltrekanterne er helt gemt bag den røde kurves tykkelse. Og det kan man, lige meget hvor tynd den røde kurve er tegnet. Derfor må grænseværdien være A.

Dette er differential- og integralregningens hovedsætning, og det er den matematiske sætning, der er vigtigst for anvendelserne. Hvis man er yderligtgående matematiker, vil man kræve et mere præcist bevis for, at det samlede areal af de små "fejltrekanter" på figuren går mod nul, men for os almindelige mennesker synes jeg, at argumentet ovenfor er overbevisende.

Udtrykket for B ovenfor skrives mere kompakt således:

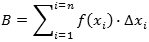
Her er det store tegn et græsk sigma. Her betyder det sum. Og det, der skal lægges sammen, er tallene f (x_i)·Δ_i, hvor i, som skrevet står, skal antage værdierne 1, 2, ... , n. Når man bruger det symbol kan hovedsætningen formuleres sådan:

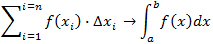
Og nu kan man forstå, hvorfor Leibniz valgte at betegne integration sådan: Integraltegnet er et stiliseret sigma, og f (x)dx minder meget om f (x_i)·Δ_i. Faktisk opfattede Leibniz dx under integraltegnet som betegnelse for en "uendelig lille" tilvækst på x. Dette lidt uldne udtryk "uendelig lille" er så i dag erstattet af en grænseovergang.

Ved anvendelserne skal man tit løse et problem, der munder ud i en sum af formen B ovenfor, også i tilfælde, hvor man overhovedet ikke er interesseret i at finde det tilsvarende areal. Der er et eksempel på det nedenfor.

Når vi nu har gjort så meget reklame for hovedsætningen, må vi hellere vise dens styrke ved at give en anvendelse i fysik:

5. En tyngdepunktsbestemmelse

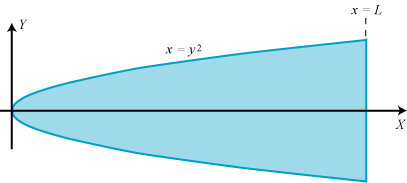
Figuren viser en tung blå plade, der er lige tynd over det hele. Den er begrænset af parablen x = y² og linien x = L. Vi vil finde ud af, hvor pladens tyngdepunkt ligger. For dem, der ikke ved, hvad et tyngdepunkt er, kan vi også sige det på en anden måde:

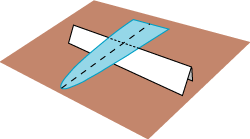Vi vil lægge pladen på en skarp ryg, som er vinkelret på parablens symmetriakse. Og så spørger vi: Hvor på pladen skal den prikkede linie placeres, hvis vi ønsker ligevægt? Det kan man finde ud af ved at dele pladen op i smalle strimler parallelt med den prikkede linie og så bruge vægtstangsreglen til bestemmelse af ligevægtsbetingelsen.

På figuren nedenfor ser vi den blå parabelplade ovenfra i to versioner. Versionen til venstre vil vi bruge til udregning af, hvor meget vægten til venstre for den punkterede linie trykker nedad, og til højre regner vi ud, hvor meget vægten til højre for den punkterede linie trykker nedad. Man skal huske, at for en vægtstang er det ikke alene vægten m, der tæller. Vægtens afstand l fra omdrejningsaksen spiller en lige så stor rolle. Det er momentet, dvs. produktet m·l, man skal regne med. Ligevægtsbetingelsen er, at summen af momenterne på den ene side af omdrejningsaksen er lig summen af momenterne på den anden side af omdrejningsaksen. a betyder afstanden fra parablens toppunkt til den punkterede omdrejningsakse, og vi lader M betegne vægten af en arealenhed af pladen. Pladen deles af omdrejningsaksen i to dele. Hver af dem deler vi nu i n smalle strimler, dem er der vist to af på figuren nedenfor. Da HTML er dårlig til at skrive kvadratrødder, skriver vi x^½ i stedet for √x. HTML er det sprog, som vi skriver hjemmesiden i.

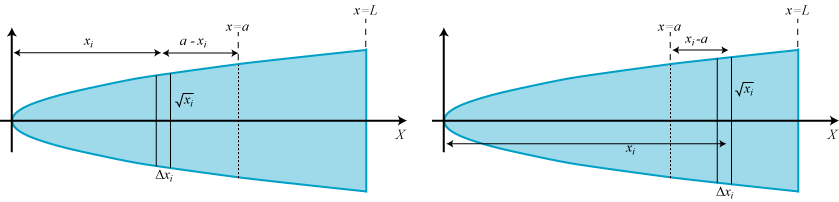
Den smalle strimmel, der er vist på figuren til venstre, har arealet 2xi½·Δxi. Strimlen har derfor vægten 2M·xi½·Δxi, og momentet bliver 2M·xi½(a-xi)·Δxi. Hvis vi adderer alle disse momenter, får vi summen

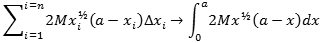Den smalle strimmel, der er vist på figuren til højre, har arealet 2xi½·Δxi. Strimlen har derfor vægten 2M·xi½·Δxi, og momentet bliver 2M·xi½(xi-a)·Δxi. Hvis vi adderer alle disse momenter, får vi summen

i begge tilfælde ifølge hovedsætningen. Ligevægtsbetingelsen bliver derfor, at differensen mellem integralerne er 0:

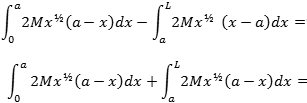
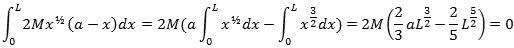
og dette er opfyldt, når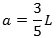

Hermed har vi fundet ligevægtsbetingelsen. For at være sikker på, at jeg havde regnet rigtigt, klippede jeg et stykke pap ud i den rigtige facon og lod det balancere på en smal kant. Og det passede præcist, som du kan se på billedet nedenfor. Der er ikke noget snyd, ikke en klat lim eller sådan noget. Det er tilfredsstillende at se, hvor godt det passer.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.