Forside Søgning Liste

Billedet ovenfor viser en vanddråbe, der ligger på en fuglefjer. Fjerens stråler ses tydeligere gennem vanddråben end ved siden af den. Vanddråben forstørrer billedet. Det må folk have lagt mærke til allerede i stenalderen, så selve linseeffekten har altid været kendt. Kunsten at lave glas opstod i Mellemøsten ca. 2500 f.Kr. Og fra det tidspunkt må man have lagt mærke til, at når man kiggede på ting gennem et buet stykke glas, blev billedet normalt forvredet, undertiden forstørret. Effekten kan meget vel være udnyttet allerede i oldtiden i form af forstørrelsesglas eller briller. Men den første dokumenterede brug af linser (i briller) siger, at Alessandro della Spina i 1284 var en af de første, der lavede briller. Hvem der startede med at lave en teori om linser, ved vi ikke. Men det må være sket ret kort tid efter, at Snell fandt brydningsloven i 1621. Her gennemgår vi den grundlæggende teori om linser.

1. Samlelinsen

Vi kigger først på en almindelig samlelinse. Linsen er af glas med brydningsforhold n. Den er begrænset af to kuglekalotter med fælles randcirkel. Vi tænker os her, at de to kugler har centre på hver sin side af linsen. Forbindelseslinien mellem centrene kaldes linsens akse. Kuglernes radier betegnes q og r. Vi forudsætter, at linsen er tynd i forhold til dens diameter, og at alle de betragtede lysstråler danner små vinkler med aksen. Vi vil bevise den fundamentale egenskab ved linser: Hvis P er en punktformet lysgiver på aksen, da vil de lysstråler fra P, der rammer linsen, brydes, så de efter linsen har et fælles punkt Q, der så kaldes billedet af P. Påstanden bevises her. Resultatet er, at når P ligger i afstanden a fra linsen, vil alle stråler ud fra P efter brydning i linsen gå gennem det punkt Q, hvis afstand b fra linsen er bestemt af formlen

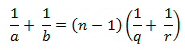
Billedet nedenfor illustrerer denne fundamentale egenskab ved samlelinser:

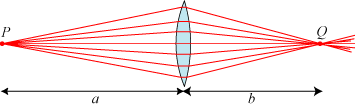
Hvis vi flytter P langt ud til venstre i det uendelig fjerne, er det et parallelbundt af stråler, der rammer linsen. Vi kan så sætte 1/a = 0 i linseformlen og finder, at dette strålebundt samles i et punkt F, hvis afstand f fra linsen er bestemt af ligningen

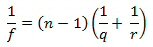
F kaldes af gode grunde linsens brændpunkt, og f dens brændvidde. Blandt børn kaldtes linsen i denne sammenhæng for et brændeglas.

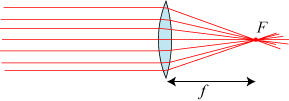
Indføres f i linseformlen, kommer den til at se sådan ud:

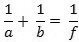Linseformlen bruges i reglen på denne form.

Hvis man vender strålegangen, fås omvendt, at en lysstråle, der udgår fra et brændpunkt, brydes, så den bliver parallel med aksen. Heraf følger igen, at forudsætningen ovenfor, om at P og Q skal ligge på hver sin side af linsen, er opfyldt, når lysgiverens afstand fra linsen er større end F.

Man kunne bruge brændvidden f som mål for linsens styrke. Men det ville være lidt akavet. For når f er lille, bryder linsen lyset meget. Derfor bruger man tallet d = 1/f som mål for linsens styrke. Enheden for linsestyrke kaldes en dioptri, og en linse siges at have styrken d dioptrier, hvis dens brændvidde er f = 1/d meter. En linses styrke i dioptrier er altså det reciprokke af dens brændvidde målt i meter. Hvis en langsynet bruger samlelinser af styrke 4 dioptrier, har linserne altså en brændvidde på 1/4 m = 25 cm.

2. Optisk midtpunkt

I beviset for, at samlelinsen danner billeder, brugte vi, at linsen er tynd, at alle stråler danner små vinkler med aksen, og at strålegangen er nogenlunde symmetrisk. Disse forudsætninger behøver vi ikke i næste afsnit.

En samlelinse har noget, der hedder et optisk midtpunkt. For at definere det tegner vi to grønne parallelle tangentplaner til linsen og kigger på en lysstråle, der inde i linsen går fra det ene røringspunkt til det andet. Den stråle krydser aksen inde i linsen, sådan som det er vist på figuren nedenfor. Det punkt, hvor strålen skærer aksen, er sort. Vi vil beregne, hvor det ligger. Vi tegner radierne til de punkter, hvor strålen går ind i og ud af linsen.

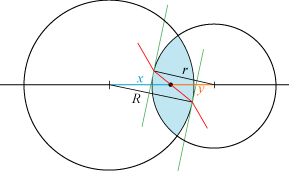
Der opstår så to trekanter, hvor radierne ligger over for det sorte punkt. Disse trekanter er ensvinklede. Derfor vil

Det sorte punkt deler altså liniestykket mellem centrene i to stykker, hvis forhold er lig forholdet mellem radierne. Det sorte punkts beliggenhed er altså uafhængigt af beliggenheden af den betragtede lysstråle. Det sorte punkt kaldes linsens optiske midtpunkt. En stråle gennem det optiske midtpunkt krydser altså linsens overflade i to punkter med parallelle tangentplaner. Som vi så ovenfor, vil en sådan stråle ikke skifte retning ved brydning i linsen, den vil kun blive parallelforskudt. Hvis vi forudsætter, at linsen er tynd nok, kan vi se bort fra denne parallelforskydning, og vi har da følgende resultat:

3. Billedkonstruktion

Vi har bevist, at under visse forudsætninger afbildes et lysende punkt på aksen af en linse i et bestemt punkt på den anden side af linsen. Under de samme forudsætninger gælder det også med god tilnærmelse, at strålerne fra et rødt lyspunkt lidt ved siden af aksen efter brydningen samles i et billedpunkt. Derfor vil en samlelinse danne et billede af en genstand, der ligger i nærheden af aksen. Vi går nu over til at fortælle, hvordan man geometrisk kan konstruere dette billede. På figurerne nedenfor viser vi en samlelinse med to sorte brændpunkter.

Vi vælger nu et objekt, der ser sådan

ud, og som har den grønne ende på aksen.

Billedet af den røde ende findes i skæringspunktet mellem (to af) følgende tre stråler:

1. En stråle fra det røde punkt, som er parallel med aksen. Efter brydningen i linsen går strålen gennem brændpunktet til højre.

2. En stråle fra det røde punkt gennem linsens optiske midtpunkt. Den går ubrudt gennem linsen.

3. En stråle fra det røde punkt gennem brændpunktet til venstre. Efter brydningen i linsen er strålen parallel med aksen.

Billedet af det grønne punkt ligger på aksen og lige så langt fra linsen som det røde billede.

Billedsekvensen nedenfor illustrerer, hvad der sker, når objektet flyttes fra det uendelig fjerne og ind mod linsen.

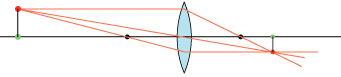	Vi starter med at placere objektet langt ude til venstre. På figuren kan man se, at billedet er omvendt, formindsket og lidt til højre for brændpunktet til højre. Når objektet rykkes nærmere linsen, rykker billedet længere væk, det er stadig omvendt og formindsket. Billedet kan opfanges på en skærm, og dets placering kan beregnes af linseformlen. På min originalfigur er med to betydende cifre a = 59 mm, b = 31 mm og f = 20 mm. Derfor er 1/a + 1/b = 0,017 + 0,032 = 0,049, mens 1/f = 0,050, en tilfredsstillende overensstemmelse.
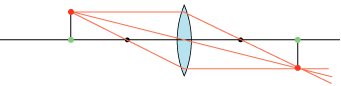	Når det grønne punkt befinder sig dobbelt så langt fra linsen som brændpunktet, er objekt og billede lige store. Billedet er stadig omvendt, og linsen er midt mellem objekt og billede. Det følger af linseformlen. Billedet kan opfanges på en skærm.
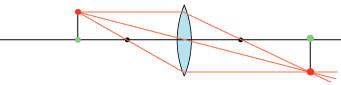	Når vi så flytter objektet længere ind mod linsen, flytter billedet længere væk fra linsen. Det bliver omvendt, forstørret og virkeligt, så det kan opfanges på en skærm. Når objektet nærmer sig brændpunktet, flytter billedet ud i det uendeligt fjerne, og dets størrelse vokser ubegrænset.
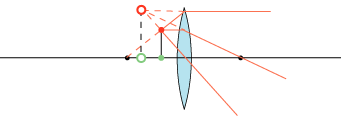	Når endelig objektet befinder sig mellem brændpunkt og linse, spreder de brudte røde stråler sig fra hinanden. De har altså intet fælles punkt. Men hvis man forlænger dem bagud, som det er vist punkteret, er der et fælles punkt. Til højre for linsen ser det altså ud, som om de røde stråler kommer fra punktet . Dette punkt kaldes et indbildt billede eller et virtuelt billede af det røde punkt. Alt i alt danner linsen et indbildt billede af hele genstanden. Billedet er opret og forstørret. Det kan ikke opfanges på en skærm, men vi kan se billedet alligevel. Øjets linse kan nemlig samle strålerne i et punkt på nethinden. Linsen virker som en lup. Placeringen kan beregnes af linseformlen, men når a < f  bliver b < 0. Afstanden til et indbildt billede skal altså regnes negativ. Det indbildte billede passerer brændpunktet, når a = ½ f.

4. Andre samlelinser

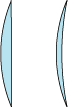Den type af samlelinser, som vi har betragtet ovenfor, kaldes i mere højtidelig sammenhæng for konvekse. Men der findes andre typer af samlelinser. På figuren vises til venstre en plankonveks samlelinse og til højre en konkavkonveks samlelinse. Linseteorien ovenfor kan tilpasses disse linsetyper. De har brændpunkter, brændvidde og optisk midtpunkt. Linseformlen gælder stadig væk, og billedet af et objekt kan konstrueres som beskrevet ovenfor. Det overlades til læseren at finde ud af, hvor det optiske midtpunkt for en plankonveks samlelinse ligger.

5. Spredelinsen

I modsætning til samlelinser er spredelinser tyndest på midten. Teorien for spredelinser kan udvikles fuldstændig analogt med teorien for samlelinser. Vi betragter kun tynde linser og kun objekter, der ligger tæt ved aksen, og vi forudsætter, at alle lysstråler danner små vinkler med aksen. Vi beviser ikke noget her, vi gengiver kun resultaterne.

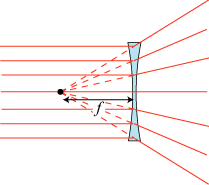Vi betragter nu en spredelinse, der er begrænset af to kuglekalotter, sådan som det er vist på figuren. Linien mellem kuglernes centre kaldes igen linsens akse. Lad os sende et bundt lysstråler, der alle er parallelle med aksen, ind mod en spredelinse. Så spredes strålerne, sådan som det er vist på figuren. De har altså ikke noget fælles punkt. Men hvis man forlænger dem bagud (vist punkteret), vil de mødes i ét punkt. Det er det sorte punkt på figuren. Det kaldes et brændpunkt, selv om der ikke er noget, der går ild i. Dets afstand fra linsen kaldes brændvidden f. I formler regnes f for at være negativ. Linsens styrke d måles i dioptrier. d defineres som d = 1/f , hvor f er målt i meter; en spredelinse har altså negativ styrke. Det bruger optikerne også i dag. Jeg er nærsynet, og mine brilleglas er f.eks. -2 dioptrier. I brugsanvisningen til mit kamera står der, at søgeren kan justeres, så man ser et skarpt billede, selv om man ikke er normalsynet. Der står:"Der kan foretages justeringer på -3,0 til +1,0 1/m (dpt)." - og det bør nu være forståeligt.

Billedet af et rødt punkt konstrueres ved en spredelinse som skæringspunkt mellem (to af) følgende 3 stråler: 1. Strålen fra det røde punkt parallel med aksen. Den brydes, så den får retning væk fra brændpunktet F1. 2. Strålen gennem det optiske midtpunkt; den går ubrudt gennem linsen. 3. Strålen, der har retning mod F2. Den brydes, så den bliver parallel med aksen.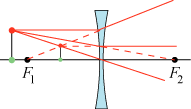

Billedet bliver opret, formindsket og indbildt, så det kan ikke opfanges på en skærm. Men det kan ses, når man kigger ind i linsen fra højre. Strålerne ser ud, som om de kommer fra billedet, men det er (på nær strålen gennem det optiske midtpunkt) kun deres punkterede forlængelser bagud, der stammer fra det røde billedpunkt. Billedet herunder er til højre set gennem mit brilleglas, som er en spredelinse. Jeg har stillet skarpt på billedet i brillen, så kan man se, hvor nyttigt det kan være at gå med briller, selv om de formindsker lidt.

Linseformlen

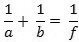
gælder også for en spredelinse. Som nævnt skal f regnes negativ. Det samme gælder b, fordi billedet er indbildt. F.eks. er, på min originaltegning til figuren ovenfor, a = 31 mm, b = -14 mm og f = -26 mm. Det giver, 1/a + 1/b = 0,071 - 0,032 = - 0,039, og det er, igen med to betydende cifre, også lig 1/f.

6. Konklusion

De første kikkerter blev konstrueret lige omkring år 1600, og brydningsloven blev fundet i 1621. Derefter blev det hurtigt klart, at det teoretiske studium af linser var en forudsætning for en forbedring af kvaliteten af briller, kikkerter og mikroskoper. Der var især to typer af fejl, som det var nødvendigt at korrigere for:

Først var der farvefejlen. Den viste sig ved, at et hvidt objekt i kikkerterne viste sig med farvede rande. Newton opdagede grunden til fejlen, og han troede fejlagtigt, at det var principielt umuligt at lave linser uden farvefejl. De første linser med stærkt reduceret farvefejl blev konstrueret af Chester Moore Hall i 1733. Man kan - i hvert fald på min skærm - ane svage farvefejl på billedet med vanddråben øverst oppe.

For det andet var der den optiske aberration (i modsætning til den astronomiske). Ovenfor måtte vi forudsætte, at linserne var tynde, og at alle de betragtede lysstråler var tæt ved at være parallelle med aksen. Og alligevel var skarpheden ikke perfekt, ikke engang teoretisk. Det viste sig senere, at man kunne forbedre billeddannelsen, bl.a. ved at bruge linseoverflader, der ikke var dele af kugleflader.

Men på trods af både teoretiske og praktiske vanskeligheder betød opfindelsen af kikkerten og mikroskopet i begyndelsen af 1600-tallet med det samme voldsomme skridt fremad i f.eks astronomi og biologi. Linser spiller stadig en stor rolle i vores daglige liv. Vi bruger briller eller kontaktlinser, vi fotograferer, selv i vores mobil er der en linse, og en power-point præsentation bliver sendt op på lærredet af en linse.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.