Vi kigger på en almindelig samlelinse. Linsen er af glas, den er begrænset af to kuglekalotter med fælles randcirkel. Vi tænker os her, at de to kugler har centre på hver sin side af linsen. Forbindelseslinien mellem centrene kaldes linsens akse. Kuglernes radier betegnes q og r. Vi forudsætter, at linsen er tynd i forhold til dens diameter, og at alle de betragtede lysstråler danner små vinkler med aksen. Vi vil bevise den fundamentale egenskab ved linser: Hvis P er en punktformet lysgiver på aksen, da vil de lysstråler fra P, der rammer linsen, brydes, så de efter linsen har et fælles punkt Q, der så kaldes billedet af P. Påstanden bevises i tilknytning til figuren nedenfor.

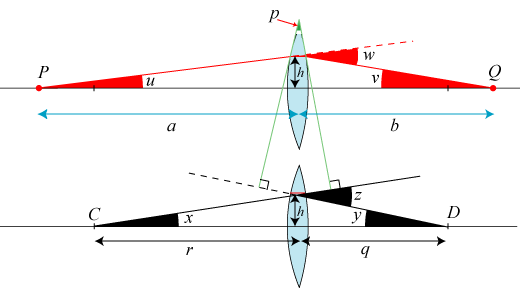
På den øverste figur har vi tegnet en rød lysstråle. Den udgår fra P, bliver brudt i linsen, og går derefter gennem Q. Vi forudsætter, at P og Q ligger på hver sin side af linsen. Tangentplanerne til linsen i de to punkter, hvor den røde stråle går ind i og ud af linsen, er tegnet grønt. De danner et prisme med brydende vinkel p. Strålen bliver brudt i linsen, ligesom den ville blive brudt i dette prisme. (Heraf følger, i parentes bemærket, at strålegangen i en linse kan vendes, ligesom den kan i et prisme.) Strålens samlede afbøjning er

under forudsætning af at vinklerne er målt i radianer.

Så kigger vi på den nederste figur. Den forestiller samme linse. C og D er de to kuglefladers centre. Den del af den røde stråle, som ligger inde i linsen, er også tegnet ind på den nederste figur. Vi tegner to radier i de begrænsende kugleflader. Den ene går fra C til den højre ende af det lille røde stykke stråle. Den anden radius går fra den anden ende af det lille røde stykke stråle og ned til D. Så er vinklen z forneden lig med vinklen p foroven. Det skyldes, at de to vinklers højre ben er vinkelrette på hinanden, og tilsvarende er venstrebenene vinkelrette på hinanden. Begge dele fordi radius og tangent til en kugleflade i samme punkt er vinkelrette på hinanden. Derfor vil

I beskrivelsen af Snells arbejder med brydningsloven fandt vi, at w = (n-1)p, hvor n er glassets brydningsforhold. Hvis vi indsætter udtrykkene for p og w i denne formel, kan vi dividere h væk og får så følgende linseformel

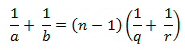
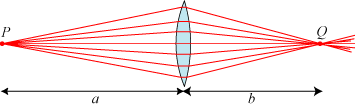
Her er n, q og r kendte størrelser. De afhænger kun af linsens form og brydningsforhold. Vi har valgt et bestemt punkt P, dvs en bestemt værdi af a. Tallet b kan så udregnes ved hjælp af formlen. Heraf følger, at man får samme beliggenhed af Q, uanset hvilken stråle ud fra P man vælger. Pointen var, at h kunne divideres væk. Alle stråler, der udgår fra P, vil altså efter brydningen i linsen gå gennem punktet Q. Dette er den fundamentale egenskab ved en samlelinse:

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.