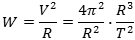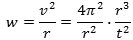Kepler fandt tre love for planeternes bevægelser, arealloven (2. lov), baneloven (1. lov) og afstandsloven (3. lov). Kepler fandt lovene empirisk, altså erfaringsmæssigt. På basis af Tycho Brahes observationer beregnede han banerne punkt for punkt og opdagede, at de inden for målenøjagtigheden passede med de 3 love. Det er naturligt, at senere fysikere på den baggrund søgte efter mere almene naturlove, der som konsekvens havde Keplers love. Mange fysikere deltog i dette arbejde, bl.a. Huygens, Wren, Hooke og Halley, men prikken over i-et var Newtons arbejder. Her skal vi ret detaljeret beskrive den sammenhæng, som Newton fandt mellem Keplers love på den ene side og gravitationsloven og Newtons bevægelseslove på den anden. Vi starter med

1. Arealloven

Keplers areallov siger, at en planet bevæger sig på en plan kurve på en sådan måde, at liniestykket fra Solen til planeten i lige lange tider overstryger lige lange arealer. Her er Newtons resultat, at arealloven er ensbetydende med, at planeten hele tiden har en acceleration rettet mod Solen. Vi viser først, at når accelerationen er rettet ind mod Solen, da gælder arealloven.

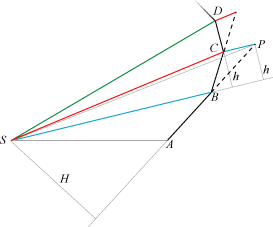Lad S være Solen, og lad os sige, at planeten til et tidspunkt er i A og i et ganske kort tidsinterval af længden Δt bevæger sig fra A til B. Arealet af trekant SAB overstryges altså på Δt sekunder. Hvis der ikke var nogen acceleration, ville planeten fortsætte med konstant hastighed, og efter endnu Δt sekunders forløb ville den være i P, hvor AB = BP. Trekanterne SAB og SBP har samme areal, fordi de har lige lange grundlinier (AB = BP) og samme højde H. Nu er der jo også en acceleration, som er rettet mod Solen. Så til flytningen fra A til B skal føjes den flytning, der sker som følge af accelerationen. Da Δt er lille, kan vi regne med, at accelerationen i det betragtede tidsinterval er konstant og parallel med BS. Så vi skal flytte P til et punkt C, der ligger sådan, at de to blå liniestykker er parallelle. (Der er tale om en addition af to flytningsvektorer, der begge kunne afsættes ud fra B). Trekanterne SAB og SBP har samme areal, og trekanterne SBP og SBC har også samme areal, da de har samme grundlinie SB og samme højde h. Så arealloven gælder for de to betragtede tidsintervaller. Nu kan man gentage argumentet med udgangspunkt i B i stedet for i A. Så får man, at arealet af trekant SCD er lig med arealet af de to andre trekanter. Sådan kan man fortsætte, og hvis man har valgt Δt enormt lille, får man fat i en krum banekurve, hvor arealloven gælder.

Vi vil ikke gennemgå beviset for, at når arealloven gælder, da vil accelerationen hele tiden være rettet mod Solen. Beviset foregår stort set på samme måde. Den eneste ændring, der sker, er, at denne gang ved man, at trekanterne SBP og SBC har samme areal, og så kan man naturligvis slutte, at de to h - er er ens.

Arealloven er altså ensbetydende med den del af gravitationsloven, der handler om gravitationens retning.

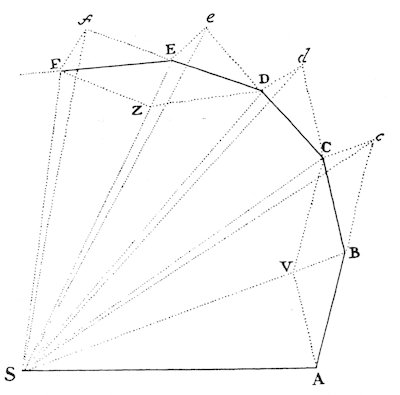
Herover viser vi den illustration fra "Principia",
som Newton brugte i sin bevisførelse.

For en planet med en cirkulær bane med centrum i Solen siger arealloven blot, at planeten bevæger sig med konstant fart. Men helt anderledes ligger det med en elliptisk kometbane. På animationen nedenfor kan man sammenligne den jævne bevægelse af Saturn i sin næsten cirkulære bane med de voldsomme hastighedsvariationer, som arealloven foreskriver i den langstrakte bane for Halleys komet:

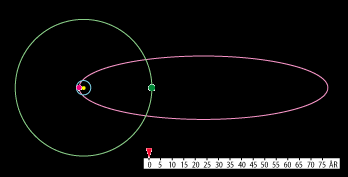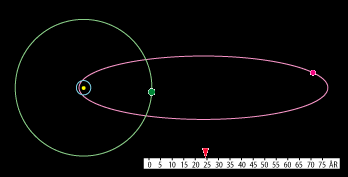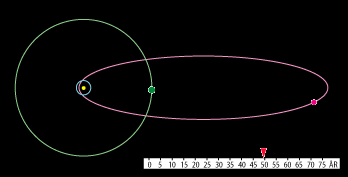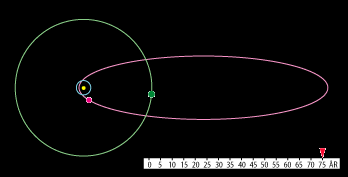
I perioden fra november 1680 til marts 1681 observerede Newton to kometer. De befandt sig på hver sin side af Solen og bevægede sig tilsyneladende i retlinede baner. Hans kollega Flamsteed overbeviste dog Newton om, at det var den samme komet, på vej mod Solen og senere på vej væk fra den. Det var den komet, som senere blev kaldt Halleys.

2. Baneloven

Nu går vi over til at behandle selve baneloven. Den siger, at planetbanerne er ellipser med Solen i det ene brændpunkt. Newton udleder ikke denne sætning af gravitationsloven, han går kun den anden vej; denne påstand er dog stadig genstand for diskussion. Det, han beviser, er, at

Beviset for denne sætning er ret kompliceret. Hvis du gerne vil se beviset, skal du klikke her.

Hvis du har været omme og se på beviset, vil du nok være enig i, at det er svært at forestille sig, hvordan Newton har fået de mange uventede ideer. Måske har han først tænkt helt anderledes og har senere fået det omsat til et formelt bevis, der fulgte tidens spilleregler. Spillereglerne sagde blandt andet, at den klassiske græske geometri var et mere solidt grundlag end den nyere analyse, som var under opbygning af Newton selv, og af Leibniz. Men tilfredsstillende kan man ikke sige, at beviset er. Man siger jo ikke, "nå derfor!" til sig selv, når man har læst beviset. "En matematisk sætning er kun helt tilfredsstillende bevist, når det er muligt at overse betydningen af hvert enkelt led i beviskæden." Det er en - ret beset menneskevenlig - tese i min ungdoms højtelskede foresattes disputats.

Newton viste også, at parabel- og hyperbelformede baner har samme egenskab som ellipserne. Han viste derimod, så vidt vi ved, ikke sætningen den anden vej. Det blev senere vist af Johann Bernoulli.

3. Afstandsloven

De to love, som vi nu har skrevet om, handler begge om, hvordan en planet bevæger sig. Først i den tredje lov sammenligner man, hvordan to planeter bevæger sig. Den tredje lov siger, at jo længere væk fra Solen en planet befinder sig, jo større omløbstid har den. Men sammenhængen mellem middelafstanden R og omløbstiden T er lidt kompliceret: Når R bliver dobbelt så stor, bliver T ganget med √8. Reglen siger, at brøken R³/T ² har samme værdi for alle planeter. Newtons undersøgelse af loven begrænser sig til cirkulære planetbaner med centrum i Solen, hvor planeten bevæger sig med konstant fart. For en sådan bevægelse er der en simpel formel for accelerationen. Formlen blev fundet af Huygens og Newton, uafhængigt af hinanden. Accelerationsformlen siger, at hvis banens radius er R, og hvis planetens fart er V, da er accelerationen rettet mod Solen og har størrelsen V²/R.

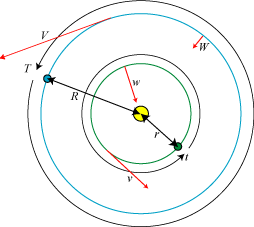Vi betragter nu to planeter, en blå med baneradius R, fart V, omløbstid T og acceleration W, og en grøn, hvor de tilsvarende størrelser betegnes med små bogstaver. Da nu V = 2πR/T får vi af accelerationsformlen, at   og     Ved division fås heraf, at

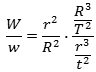Af denne formel aflæses følgende to resultater:

Hvis accelerationerne forholder sig omvendt af afstandenes kvadrat, vil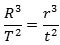

Hvis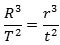

vil accelerationerne forholde sig omvendt af afstandenes kvadrat.

Afstandsloven er altså ensbetydende med, at planeternes accelerationer aftager med kvadratet på afstanden til Solen.

4. Konklusion

Alle de ting, vi har vist her på siden, passer med gravitationsloven. Dels siger den jo, at kraften - og dermed accelerationen - er rettet mod Solen, og dels har den i udtrykket for kraften et R² i nævneren. Så Newton har fundet to almene naturlove, nemlig gravitationsloven og Newtons 2. lov, der som konsekvens har Keplers love.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.