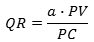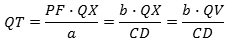Vi giver her Newtons eget bevis for baneloven. Newton viser følgende: Når en planet bevæger sig i en ellipsebane med Solen i et brændpunkt, og når dens acceleration hele tiden er rettet mod Solen, da er dens acceleration omvendt proportional med kvadratet på afstanden til Solen.

Newton starter sit bevis med følgende hjælpesætning. (I matematikken kalder man et resultat, som er uden større selvstændig betydning, men som er af afgørende betydning for beviset for en vigtig sætning, for et lemma.) Altså:

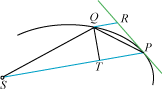Lemma: Vi betragter et punkt, der bevæger sig på en plan kurve, sådan at accelerationen hele tiden er rettet mod et center S. I et kort tidsinterval Δt bevæger punktet sig fra P til Q. R vælges på tangenten i P, sådan at de to blå linier er parallelle, og T vælges, så QT er vinkelret på SP. Da er accelerationen omvendt proportional med

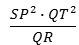Påstanden betyder, at der findes en konstant k, så accelerationen har størrelsen

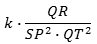
Her afhænger k ikke af beliggenheden af P og Q på kurven.

Formlerne skal forstås således, at Δt skal være valgt så lille, at brøkerne er lig deres grænseværdi for Δt → 0. Man kan også sige, at brøkerne er lig deres grænseværdi, når Q nærmer sig ubegrænset til P. Man kan ikke på dette udtryk se, hvad denne grænseværdi er, det finder vi ud af nedenfor.

Det er interessant, at Newton omtaler brøken (SP ²·QT ²)/QR som et legeme, i originalen på latin "solidum". Det er i overensstemmelse med traditionen fra den græske oldtid, hvor man ikke opfattede størrelser som tal, men som geometriske figurer. Betegnelsen solidum stemmer med, at brøken har dimensionen L³, altså en længde i tredie.

Newtons bevis er vanskeligt at forstå. Vi giver her en version, som vores kilde, Dugas, fandt det nødvendigt at udarbejde: Som oppe under arealloven er PR den flytning, som punktet ville få, hvis det fortsatte med uændret fart fra P i Δt sekunder. Og QR er den flytning, der samtidig sker på grund af accelerationen, som har størrelse w. Da Δt er lille, kan vi regne w for konstant under bevægelsen fra P til Q. Ifølge Galilei vil så QR = ½wΔt². Arealet af trekant SPQ er ½SP·QT, og ifølge arealloven er dette produkt proportionalt med Δt. Accelerationen bliver altså

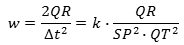
Hermed er lemmaet bevist.

Nu går vi over til at behandle selve baneloven. Den siger, at planetbanerne er ellipser med Solen i det ene brændpunkt. Newton udleder ikke denne sætning af gravitationsloven, han går kun den anden vej; denne påstand er dog stadig genstand for diskussion. Det han beviser er, at

Undervejs i beviset benyttes tre sætninger om ellipser, som ikke er så velkendte. Du kan se sætningerne her. Beviset foregår sådan, tag en dyb indånding først:

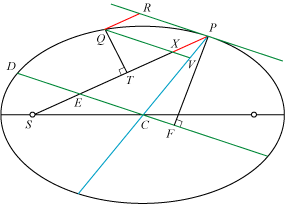Figuren viser en ellipse med halvakser a og b. Den grønne diameter er valgt, så den er parallel med tangenten i P. Det tager en ganske kort tid Δt for punktet at bevæge sig fra P til Q. RQ er som før den flytning, der skyldes accelerationen. Derfor er de røde liniestykket parallelle; det er de grønne også, sådan er QXV tegnet. Den blå diameter er konjugeret med den grønne. Da firkant PRQX er et parallellogram, og da trekanterne PXV og PEC er ensvinklede, vil ifølge sætning 1 XP/PV = QR/PV = a/PC. Trekanterne QTX og PFE er også ensvinklede. Derfor er (igen ifølge sætning 1) QX/QT = a/PF. Ifølge sætning 3 er ab = PF·CD. Af disse formler fås, at og

Det sidste lighedstegn er lidt speget. Det er jo oplagt forkert, at QX = QV. Men i grænsen, når Q nærmer sig ubegrænset til P, vil XV være forsvindende lille, selv i forhold til QX. Det skyldes, at når Q nærmer sig P, vil Q nærme sig meget hurtigere til tangenten end til P. Det betyder noget i retning af, at hvis QX er nul komma x nuller én , da vil XV have størrelsesordenen nul komma 2x nuller én fra tangenten. Princippet er en sag, der først blev fuldt afklaret af matematikere i slutningen af 1800-tallet. Men fra nu af tænker vi os, at Δt er valgt så lille, at QX = QV.

Ifølge lemmaet skal vi undersøge forholdet

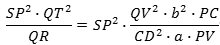
Ifølge sætning 2 vil

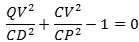
der omskrives til

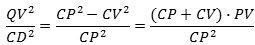
Nu kan vi endelig finde den søgte værdi af lemmaets forhold:

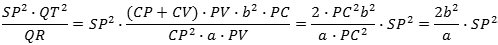
og dette udtrykker ifølge lemmaet, at accelerationen er omvendt proportional med kvadratet på afstanden SP. Hermed er beviset fuldført. Det næstsidste lighedstegn er rigtigt, fordi Δt er så lille, at vi kan sætte CV = CP.

Ja, det er godt nok bevist, men det er svært at forestille sig, hvordan Newton har fået de mange uventede ideer. Måske har han først tænkt helt anderledes, og har senere fået det omsat til et formelt bevis, der fulgte tidens spilleregler. Spillereglerne sagde blandt andet, at den klassiske græske geometri var et mere solidt grundlag end den nyere analyse, som var under opbygning af Newton selv, og af Leibniz.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.