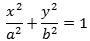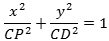På denne side formulerer vi tre sætninger om ellipser, som Newton brugte i sine undersøgelser af sammenhængen mellem Keplers love for planetbevægelserne og gravitationsloven. Sætningerne var kendt i græsk oldtid. Vi beviser kun en af sætningerne.

Sætningerne handler alle om det begreb, som hedder konjugerede diametre i en ellipse. Så det starter vi med at definere.

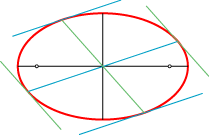Et liniestykke kaldes en diameter i en ellipse, hvis endepunkterne ligger på ellipsen, og ellipsens centrum ligger på liniestykket. På figuren er der tegnet 4 diametre. Nu kigger vi på den blå diameter. I dens endepunkter har vi tegnet to grønne tangenter. Og så har vi med grønt tegnet den diameter, der er parallel med de grønne tangenter. Den grønne diameter kaldes så konjugeret til den blå. Og så ligger landet så pænt, at ellipsens tangenter i endepunkterne af den grønne diameter automatisk bliver parallelle med den blå diameter. Så den blå diameter er konjugeret til den grønne. De to diametre kaldes derfor bare konjugerede. Specielt er de to sorte diametre konjugerede. Der er ingen simpel regel om, hvilke vinkler to konjugerede diametre danner med hinanden eller med ellipsens symmetriakser.

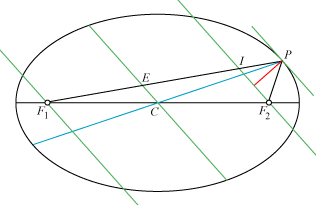
Sætning 1. På figuren er den grønne og den blå diameter konjugerede. Brændstrålen PF1 skærer den grønne diameter i E. Så er PE = a, altså lig med ellipsens halve storakse. Sætningen er let at bevise. De fire grønne linier er tegnet parallelle. Det røde liniestykke er tegnet vinkelret på de grønne linier, så det røde liniestykke halverer vinklen mellem de to brændstråler. Derfor er PI=PF2. De to yderste lange grønne linier ligger lige langt fra den midterste. Derfor er E midtpunkt af IF1. Ifølge definitionen af en ellipse er summen af de to brændstråler 2a. Den består af to lige lange stykker og to lige korte stykker. Så et langt og et kort, dvs PE, er a.

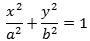
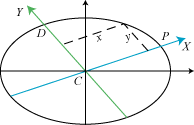
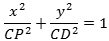
I standardbeliggenheden i et koordinatsystem er ligningen for en ellipse Hvis ellipsen ligger på en anden måde i koordinatsystemet, bliver ligningen næsten altid mere kompliceret. Men der er en ejendommelig undtagelse, som er vist på figuren: Sætning 2. Når man benytter et skævvinklet koordinatsystem med et par konjugerede diametre som koordinatakser, bliver ellipsens ligning Ligningerne er altså formelt identiske, men læg mærke til, at koordinaterne x og y måles parallelt med de farvede koordinatakser X og Y.

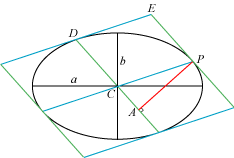
Sætning 3a. På figuren til højre er den blå og den grønne diameter konjugerede. Da er ab = CD·PA. Det er den formel, vi får brug for, men sætningen har et smukkere indhold: CD·PA er arealet af rektanglet PCDE, altså en fjerdedel af det store parallellograms areal. Så sætningen kan også formuleres sådan: Sætning 3b. Alle de parallellogrammer, der udspændes af par af konjugerede diametre, har samme areal, nemlig 4ab.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.