Forside Søgning Liste

Vi skal her betragte den grundlæggende matematiske teori for tandhjul. Set fra et overordnet principielt synspunkt bør to tandhjul i indgreb opfylde følgende tre betingelser:

1. Når det ene tandhjul drejer med konstant vinkelhastighed, da skal det andet også dreje sig med konstant vinkelhastighed.
2. Når det ene tandhjul står stille, må det andet ikke kunne rokkes en tøddel.
3. Tænderne skal rulle på hinanden, der må ikke være gnidning.

Når den første betingelse er opfyldt, findes der to cirkler med centrer fælles med hver sit tandhjul, der ruller på hinanden under bevægelsen. Forholdet mellem radierne er det omvendte af forholdet mellem vinkelhastighederne, og summen af radierne skal være afstanden mellem tandhjulenes centre. Disse cirkler kaldes rullecirklerne.

I møller brugtes tandhjul allerede i middelalderen. De tandhjul, man brugte der, opfyldte ingen af de tre betingelser. De var lavet af træ. I oldtiden fandtes der mekanismer med tandhjul af metal, men der kendes ingen teoretisk behandling af tandhjul, før Ole Rømer i 1675 gav en matematisk beskrivelse af en tandhjulsform, der opfylder de to første betingelser. Os bekendt er det, vi skriver her, det første forsøg på at rekonstruere Rømers tandhjulskonstruktion og dets formål.

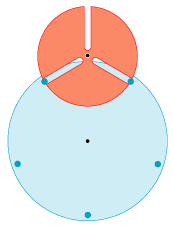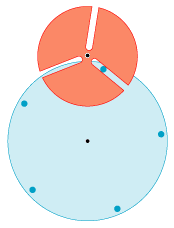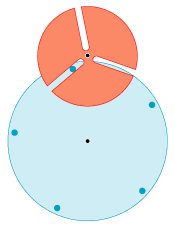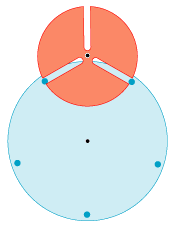Til sagen: Animationen til venstre illustrerer problemstillingen. Det øverste røde tandhjul har tre slidser. I dem passer fem små cylindre, der sidder fast på oversiden af det blå tandhjul. Det blå tandhjul drejer med konstant vinkelhastighed, og resultatet er, at det røde tandhjul tvinges til at dreje med stærkt varierende vinkelhastighed. Man kan argumentere for, at det vil være sådan, uanset tandformen: Når en tand på et blåt tandhjul skubber på et rødt tandhjul med den yderste spids af en tand, så må det af to grunde give det røde tandhjul større vinkelhastighed, end når en blå tand slipper indgrebet: For det første vil en bestemt flytning af den blå tandspids bevirke større rød rotation, når flytningen finder sted nær det røde centrum, end når den finder sted længere ude. Og for det andet sker flytningen, lige før indgrebet slipper, i retning af en rød radius, og så giver det jo slet intet bidrag til den røde vinkelhastighed. Rømer opdagede, at dette argument er forkert, og angav som nævnt en tandform, der opfylder tandhjulsbetingelserne 1 og 2.

Rømer benyttede epicykloider og retlinede hypocykloider i sin tandhjulskonstruktion. Nu skal vi forklare, hvad epi- og hypocykloider er for nogen.

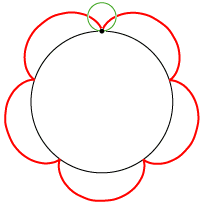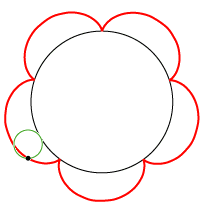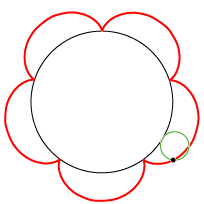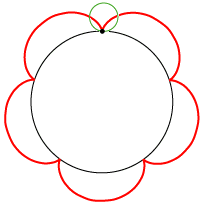
En epicykloide er banekurve for et punkt på en cirkel, der ruller på ydersiden af en anden cirkel. Animationen til venstre viser et eksempel. Der er et sort punkt på en lille grøn cirkel, og cirklen ruller på ydersiden af den sorte cirkel. Så gennemløber det sorte punkt den røde epicykloide. Når vi siger ruller, mener vi uden at glide. Røringspunktet mellem de to cirkler gennemløber altså i samme tid lige lange buer på den grønne og den sorte cirkel. Til højre viser vi tilsvarende, hvordan en hypocykloide dannes. Denne gang ruller den grønne cirkel på indersiden af den sorte. Radius i den sorte cirkel til venstre er fem gange så stor som radius i den grønne cirkel, mens radius i den sorte cirkel til højre er tre gange så stor som radius i den grønne cirkel. Der er et interessant specialtilfælde: Hvis vi til højre vælger den sorte cirkels radius dobbelt så stor som den grønnes, kan man vise, at hypocykloiden (lidt overraskende) bliver en to gange gennemløbet diameter i den sorte cirkel. Vi får nedenfor brug for dette specielle tilfælde. Her er radierne i de sorte cirkler henholdsvis fem og tre gange så store som radius i den grønne cirkel, men der behøver ikke at være sådanne simple talforhold. I det specielle tilfælde, hvor den lille cirkels radius er halvt så stor som den stores, kan man bevise, at hypocykloiden bliver en diameter i den store cirkel. Som vi skal se længere nede, benyttede Rømer i det bevarede materiale kun denne specielle slags hypocykloider, men vi starter med at beskrive sagen i det almene tilfælde.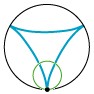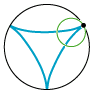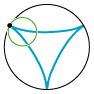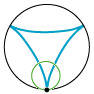

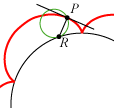Figurerne viser en egenskab ved cykloiderne, som vi bruger nedenfor: I begge tilfælde er bevægelsen en rulning om røringspunktet R. Det lyder derfor rimeligt, at cykloidens tangent i punktet P er vinkelret på PR. Og det er faktisk rigtigt. Det bevises i den matematiske disciplin, der hedder kinematik.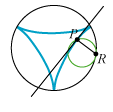

Nu kommer vi så til Rømers gode ide:

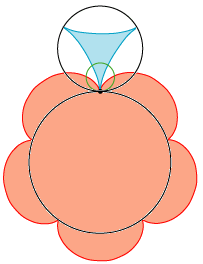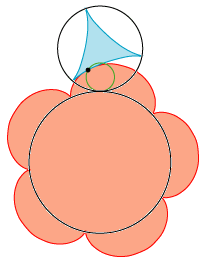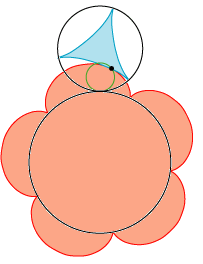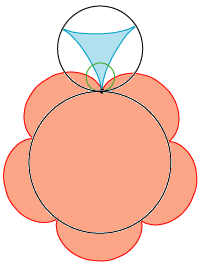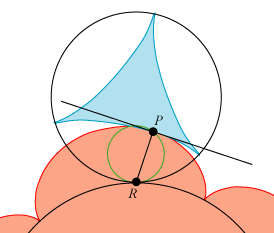På animationen til venstre er de to sorte cirkler, som vi benyttede ovenfor, anbragt, så de rører hinanden udvendigt. Vi tænker os, at de sorte cirkler, basiscirklerne, ruller på hinanden, så cirkelpunkterne passerer røringspunktet i retning mod venstre. Den lille grønne cirkel, rullecirklen, lader vi rulle mod højre på de sorte cirkler, så hurtigt, at den alt i alt ikke flytter sig. Dens vinkelhastighed skal være 3 gange så stor som den lille cirkels, og 5 gange så stor som den stores. Det sorte punkt vil så frembringe begge cykloider. Det ser jo nydeligt ud, når jeg selv skal sige det. Hovedpointen, Rømers opdagelse, er illustreret på stillbilledet til højre: Som nævnt ovenfor er begge cykloiders tangenter i punktet P vinkelrette på RP. De to tangenter er altså sammenfaldende, og det viser, at under hele den jævne bevægelse rører de to cykloider hinanden. Og det er jo lige det, vi har brug for, når vi skal lave tandhjul. Selv om en ingeniør næppe vil være begejstret for den tekniske anvendelighed, synes jeg godt, at vi kan være stolte på Rømers vegne: Animationen til venstre viser to "tandhjul", der begge drejer sig med konstant vinkelhastighed, og som hele tiden rører hinanden! Men læg mærke til, at de to tandhjul ikke ruller på hinanden, der finder gnidning sted.

Der er flere grunde til gåseøjnene. Én er, at når de to cykloider rører hinanden i et punkt midt mellem spidserne, så vil en kraftoverførsel fra det ene tandhjul til det andet være håbløs. Det er faktisk kun, når spidserne er tæt ved hinanden, at der er mulighed for en fornuftig kraftoverførsel. En anden grund er, at det ene tandhjul ikke fastholder det andet i en bestemt stilling. På figuren ovenfor til højre kan man fastholde det blå tandhjul og så alligevel dreje det røde et stykke mod uret. Man kan fjerne disse ulemper og samtidig beholde den grundlæggende ide ved at gøre to nye tiltag:

For det første kan man supplere med de to nye cykloider, der er vist på figuren til venstre. Det er en grøn epicykloide og en brun hypocykloide. De frembringes, når den sædvanlige lille grønne cirkel ruller indeni den store sorte cirkel og udenpå den lille. For det andet behøver man ikke at bruge hele cykloider, man kan i stedet bruge små brudstykker, hentet i nærheden af spidserne.

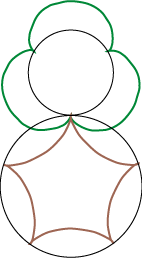
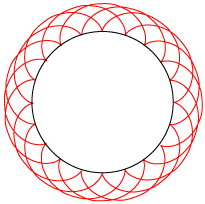
Vi beslutter os nu til, at det store tandhjul skal have 10 tænder og det lille 6. Tandantallene skal naturligvis have samme forhold som cirklernes radier. Vi starter med at vise, hvordan tandhjulenes tænder opbygges af små stykker af cykloidebuer, hentet i nærheden af spidserne. Vi starter med det store tandhjul.

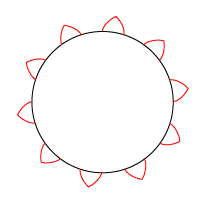
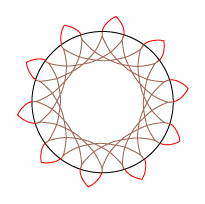
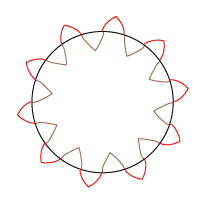
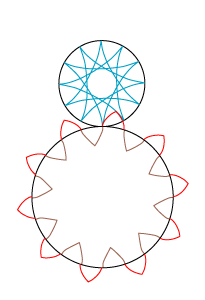
Vi tegner 4 eksemplarer af den røde epicykloide uden om den store sorte cirkel. To naboeksemplarer er forskudt 18° i forhold til hinanden.	Og så beholder vi kun de 20 cykloidestumper, som er vist her. De skal være spidser på det færdige tandhjul. De 18° gjorde, at der blev 10 tænder på tandhjulet.	Så tegner vi 4 eksemplarer af den brune hypocykloide inde i den sorte cirkel. Spidserne skal falde sammen med epicykloidens spidser.	Også her beholder vi kun de viste 20 cykloidestumper. Og så er det store tandhjul færdigt med 10 tænder.

Vi går nu over til at beskrive opbygningen af det lille tandhjul.

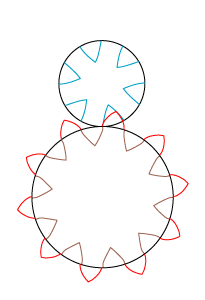
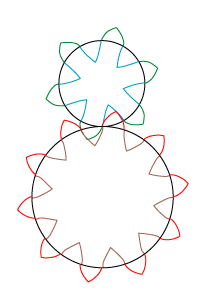
Vi tegner 4 eksemplarer af den blå hypocykloide inde i den lille sorte cirkel. To naboeksemplarer er forskudt 30° i forhold til hinanden. Cykloiderne er placeret sådan, at der forneden er en blå spids, der falder sammen med endepunktet af en rød bue. Det betyder, ifølge Rømers gode ide, at hvis man drejer tandhjulene lidt (med de rigtige vinkelhastigheder), så spidsen og det røde punkt flytter mod venstre, så vil en rød og en blå bue røre hinanden. Det er pointen i hele konstruktionen.	Og så beholder vi kun de 12 cykloidestumper, som er vist her. De skal være bunden af tandmellemrummene på det færdige tandhjul. De 30° gjorde, at der blev 6 tænder på tandhjulet.	Så tegner vi 4 eksemplarer af den grønne epicykloide uden om den sorte cirkel. Spidserne skal falde sammen med hypocykloidens spidser.	Også her beholder vi kun de viste 12 cykloidestumper. Og så er det lille tandhjul færdigt med 16 tænder. Vi sætter nu tandhjulene i gang med vinkelhastigheder, der forholder sig som 5 til 3, og så tænderne i indgreb flytter mod venstre. Så vil som nævnt en rød og en blå bue røre hinanden under bevægelsen. Og når det er slut, vil en grøn og en brun bue af samme grund røre hinanden under den fortsatte bevægelse. Faktisk vil der hele tiden være to eller tre berøringspunkter mellem tandhjulene. Så det ene tandhjuls stilling bestemmer entydigt det andets. Den anden tandhjulsbetingelse er altså opfyldt i dette tilfælde.

På animationen nedenfor viser vi resultatet, to tandhjul, der begge drejer med konstant vinkelhastighed, og som fastholder hinanden på en sådan måde, at det enes stilling entydigt bestemmer det andets:

Rømers tandhjulskonstruktion vakte opmærksomhed i den videnskabelige verden. I breve fra Leibniz og Huygens til Rømer omtales konstruktionen rosende, og der er anbefaling til Rømer om at få det offentliggjort. Rømer fik det imidlertid aldrig skrevet ned, og der er intet bevaret om sagen fra hans hånd. Når vi alligevel kan udtale os sikkert om, hvad der var Rømers bidrag, skyldes det, at Huygens i et manuskript fra 1678 kopierede nogle af Rømers tandhjulstegninger og gav en kortfattet beskrivelse af sagen. Vi viser nedenfor til venstre en af de bedste af Huygens tegninger. Som figurtekst skrev Huygens på latin, her i oversættelse: "Rømers hjul i overensstemmelse med beskrivelsen af epicyklerne."

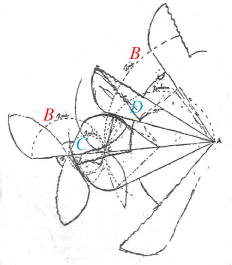Selv om tegningen ser noget skitseagtig ud, kan man godt se, hvad der foregår. Det er mig, der har tilføjet de farvede bogstaver. Basiscirklerne er markeret med et B. Cykloiderne dannes, når rullecirklerne mærket C og D ruller på basiscirklerne. Konstruktionen foregår, som det er beskrevet ovenfor, idet det dog kun er den ene side af tænderne, der beskrives. Rullecirklen mærket C er halvt så stor som den lille basiscirkel. Derfor bliver hypocykloiden som nævnt en diameter i den lille basiscirkel. Tilsvarende er den store rullecirkel D halvt så stor som den store basiscirkel, så ved rulningen dannes der tilsvarende en diameter i den store basiscirkel. Rømer har nok valgt det sådan, fordi det vil lette fremstillingen af tandhjulene, at man vælger hypocykloiderne som liniestykker. Hvis tænderne skal kunne komme til for hinanden, er det kun ret små cykloidedele, der kan benyttes. Vi gengiver eksemplet her, fordi det dokumenterer, at det er Rømer, der har opfundet epicykloidefortandingen.

Animationen her viser, hvordan Rømers tegning skal fortolkes. Sådan som tænderne er antydet på figuren ovenfor, er der ikke plads til dem. Det er nok derfor, Huygens har tegnet begrænsningslinier bugtede. Det betyder: "Jeg ved ikke rigtigt, hvor denne linie skal tegnes." På animationen viser vi i overensstemmelse med tegningen kun tændernes begrænsning til den ene side. Når man betragter animationen, kan man godt undre sig over, at vinkelhastighederne er konstante. Den måde, tænderne skubber til hinanden på, veksler jo hele tiden. På animationen viser vi også, at røringspunkterne mellem tænderne hele tiden ligger på rullecirklerne.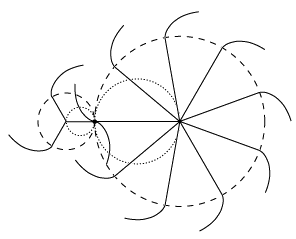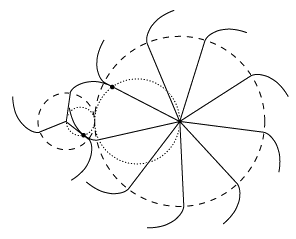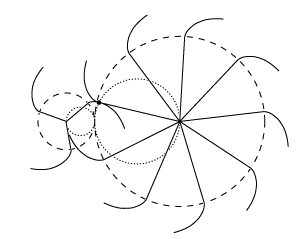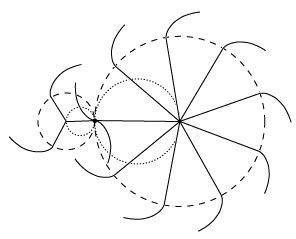

Huygens tegning efter Rømer er faktisk konstruktionstegning for de to tandhjul, der er vist på animationen ovenfor

På Huygens´ tegning vises kun den ene side af tandhjulenes tænder. Til højre viser vi en anden af de tegninger, som Huygens tegnede efter Rømers forlæg. Den viser et komplet tandhjul. Spidserne er dele af epicykloider, mens det inderste af tænderne er begrænset af dele af retlinede hypocykloider. Ligheden med animationen ovenfor er stor.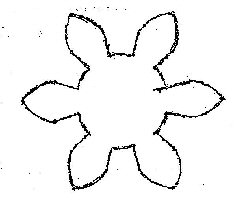

Alt det ovenstående handler kun om teori. Derfor vil det være rimeligt inden vi slutter at spørge, om Rømers tandhjulskonstruktion blev brugt i praksis. Svaret er sandsynligvis et ja. Billedet nedenfor viser et tandhjul fra et ur på museet Kroppedal. Uret kaldes Rømers Ur. Det er fremstillet i Paris af urmager Isaac Thuret (1630 — 1706), som Rømer arbejdede sammen med. Det fremgår af billederne, at Rømer faktisk fik fremstillet tandhjul, efter det ovenfor beskrevne princip.

Her kunne vi godt stoppe gennemgangen af Rømers tandhjul, men i Huygens´ manuskript er der et stykke tekst om en interessant forenkling, som vi her til slut vil kommentere.

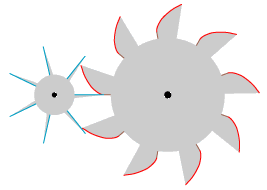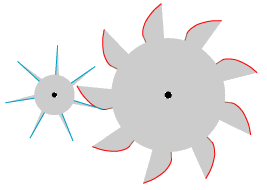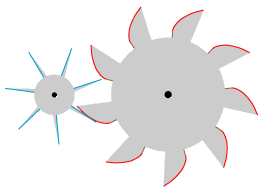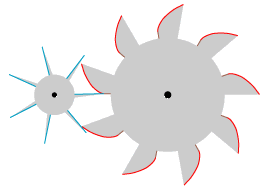
Ud over ovennævnte latinske tekst ledsages figuren ovenfor i Huygens manuskript nemlig af en kort tekst på fransk. Vi har haft besvær med oversættelsen, men vi mener, at der står følgende: "Når det drejer sig om et tandhjul med mere end 4 tænder, som er bevæget af et hjul, så burde man fjerne epicykloiderne fra tænderne og kun beholde de rette linier fra centrum, så der kun bliver presset på den rette linie AB. Så vil den værste gnidning blive fjernet." Teksten kræver lidt fortolkning: "hjul" må være det store tandhjul til højre, og resten af teksten handler kun om det lille tandhjul. "på den rette linie AB" må være "efter passage af centerlinien AB". Ideen er, at man fjerner epicykloiderne på det lille tandhjul, så der kun er de retlinede hypocykloider tilbage. Det har den konsekvens, at der ikke er brug for hypocykloiderne på det store tandhjul. Med disse fortolkninger, og med 7 tænder på det lille tandhjul, viser vi på animationen til venstre, hvad der kommer ud af teksten, idet vi, som ovenfor, kun viser den ene side af tænderne. Det er vist rigtigt nok, at der bliver mindre gnidning, end der var, da epicykloiderne var med. Der kunne være en anden attraktion: Med den tids teknologi må et tandhjul med retlinede tænder have været lettere at fremstille end et med krumme tænder.

Ovenfor har vi kun vist den ene side af tænderne. Vi viser her, hvordan det kan komme til at se ud, når man tegner begge sider af tænderne. På det store tandhjul har vi valgt 20° pr. tand. Heraf har vi brugt 5° til et mellemrum mellem de krumme tænder. Så opnår vi, at de retlinede tænder på det lille tandhjul får en acceptabel bredde.

Knap 100 år efter at Rømer havde fundet sin tandhjulskonstruktion, arbejdede den schweiziske matematiker Leonhard Euler med tandhjulsformer. Det lykkedes for Euler at konstruere et par tandhjul, der begge drejer sig med konstant vinkelhastighed, og hvor det ene tandhjuls tænder er rette linjestykker på linjer gennem centrum. Denne konstruktion var let at lave for Rømer. På animationen ovenfor skulle han bare smalne de retlinede tænder, så de blev erstattet af linjestykker. Vi viser et muligt resultat på animationen til højre.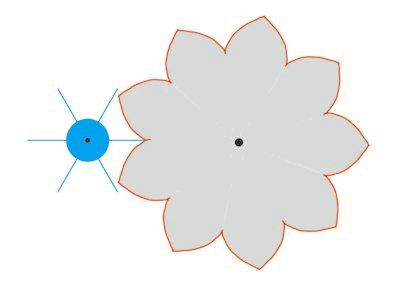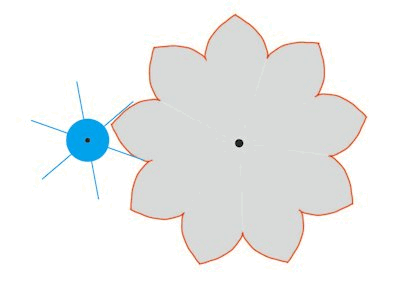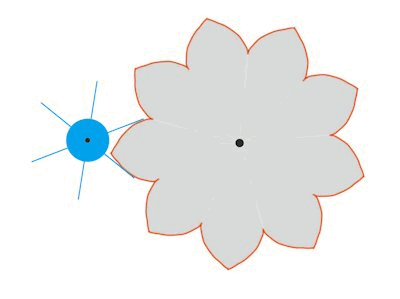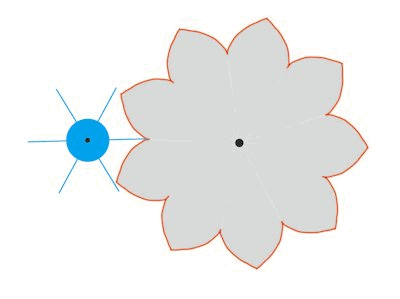

Man kunne også have det ønske, at tænderne på de to tandhjul rullede på hinanden, så der ikke var nogen friktion. Man kan imidlertid matematisk bevise, at når de to vinkelhastigheder er konstante, så kan det ikke lade sig gøre. Der er nemlig i matematisk kinematik en sætning, der siger, at bevægelsen af tandhjulene kun på én måde kan beskrives som en rulning. Og da rullecirklerne ruller på hinanden, kan tandhjulene ikke rulle på hinanden.

Vi har fundet to steder, hvor det påstås, at Rømer lavede cykloideformede tandhjul, hvor tænderne ruller på hinanden. Påstanden er næppe rigtig. Hvis man f.eks. ændrer bevægelsen af den røde og den blå cykloide ovenfor til en rulning, der starter med sammenfaldende spidser, så vil de to cirklers centre få varierende afstand, så det bliver der ikke noget tandhjul ud af. Hvis man dropper kravet om konstante vinkelhastigheder, kan man godt lave tandhjul, der ruller på hinanden. Du kan se et eksempel på, hvordan det kan foregå her.

Vi skulle måske nævne, at cykloidefortanding sjældent bruges i vore dage. Der er mange andre tandformer, som matematisk er lige så gode, men som teknisk er bedre.

Vi kender ikke meget til, om rømerske tandhjul blev brugt i praksis efter hans død. De omtales dog i den store franske encyklopædi. I 1765 udkom bind 21, dvs plancebind 4. Hvis man her søger under Horologie finder man på planche 19 billedet herunder:

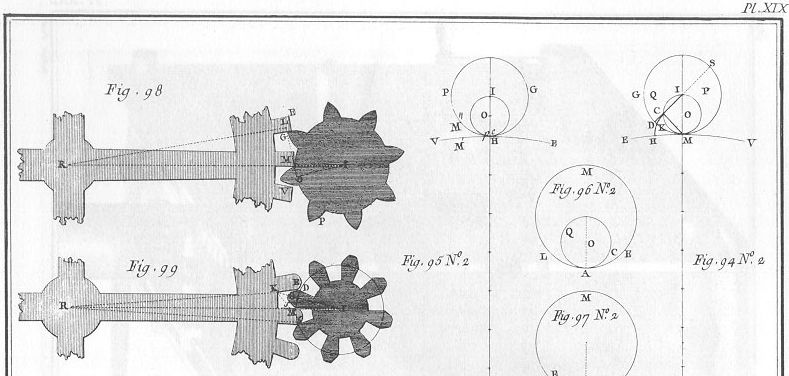
Begge de to tandhjulspar her er klart rømerske, af typer, som vi har beskrevet ovenfor. Så Rømerske tandhjul har været kendt i videnskabelige kredse i Frankrig i midten af 1700-tallet. Til højre for tandhjulsparrene ses den geometriske konstruktion af tændernes form. Der er små fejl på tegningerne.

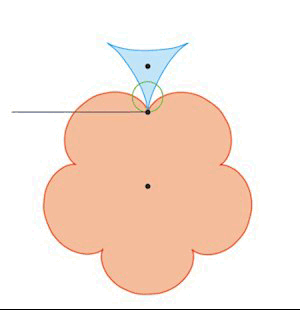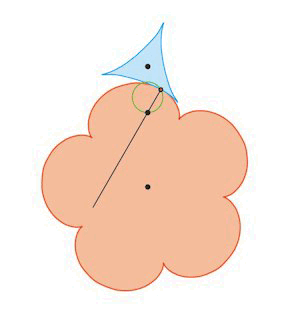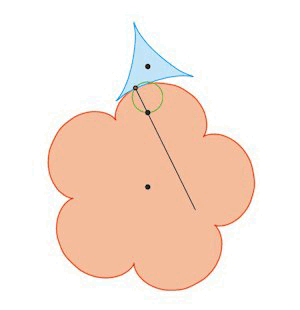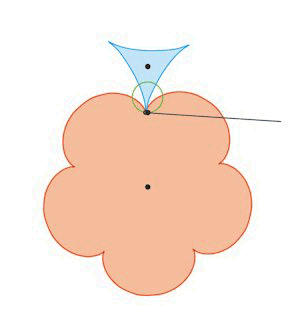
Figuren til venstre er en gentagelse af en af figurerne ovenfor. Det fremgår af denne figur, at normalen til fællestangenten for de to kurver i røringspunktet P hele tiden går gennem det faste punkt R. På figuren til højre viser vi hvordan normalens bevægelse ser ud. Denne iagttagelse kan du læse meget mere om i vores omtale af de tandhjul, som Euler konstruerede.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.