Vi går nu - vi indrømmer, at det er en sidebemærkning - over til at vise, at hvis man dropper ønsket om konstante vinkelhastigheder, kan man lave tandhjul, der ruller på hinanden. Animationen nedenfor viser et eksempel:

Læg mærke til, at hvis det ene tandhjul stoppes, så vil det andet i næsten alle stillinger kunne drejes lidt frem og tilbage. - Animationen er ikke i sig selv et bevis for, at det kan lade sig gøre at lave rullende tandhjul. Vi får brug for noget matematik for at kunne gennemføre konstruktionen, og beskrivelsen her henvender sig til læsere med en uddannelse i matematik.

I den matematiske kinematik betragter man en fast plan og en bevægelig plan, der falder sammen. Man kan tænke sig den faste plan som overfladen af et bord og den bevægelige plan som et stort stykke papir, der glider rundt på bordet. Vi betragter i det følgende en bestemt bevægelse af den bevægelige plan, og vi ser bort fra det tilfælde, hvor der er et tidspunkt, hvor alle hastighedsvektorer er ens. Så findes der til ethvert tidspunkt et og kun ét punkt i den bevægelige plan, der har fart 0. Det kaldes det øjeblikkelige drejningspunkt og betegnes Ø. Så vil hastighedsvektorerne til det tidspunkt være som i en drejning om Ø med en passende vinkelhastighed. Ø vil beskrive en kurve i den faste plan. Den kaldes den faste polkurve. Ø beskriver også en kurve i den bevægelige plan. Den kaldes den rullende polkurve. Man kan så bevise, dels, at den betragtede bevægelse kan fremkomme ved, at den rullende polkurve ruller på den faste polkurve, og dels, at bevægelsen ikke på andre måder kan beskrives som en rulning. Teorien findes i lærebøger i differentialgeometri og i kinematik, se referencerne.

Principielt er det nu let at se, at man kan lave rullende tandhjul: Vælg en konstant vinkelhastighed for det ene tandhjul og en hvilken som helst variabel vinkelhastighed for det andet. Så kan den relative bevægelse af de to tandhjul beskrives som en rulning af to kurver på hinanden, og disse kurver er så tandhjulsformerne. Denne procedure følger jeg nu i beskrivelsen af, hvordan animationen ovenfor er konstrueret.

Ved beskrivelsen af, hvordan tandhjulene geometrisk konstrueres, er det hensigtsmæssigt at antage, at det store tandhjul ikke drejer, mens det lille både drejer rundt om det store og om sig selv. Det store tandhjul ligger altså i en fast plan, og det lille ligger i en bevægelig plan, der falder sammen med den faste. Som udgangspunkt for vores tandhjulskonstruktion tegner vi to cirkler, der rører hinanden: En cirkel med radius R i den faste plan og en cirkel med radius r i den bevægelige plan. Forholdet mellem R og r er lig forholdet mellem antallene af tænder på de to tandhjul. På figuren bevæger den store cirkel sig altså ikke. Linien CD med den lille cirkel starter lodret for t = 0 og drejer om C med konstant vinkelhastighed ω. Derudover drejer den lille cirkel sig om sit centrum med vinkelhastighed ω1. Hvis ω1 er konstant, kan bevægelsen beskrives ved, at en cirkel ruller på en anden, og så kan tænderne ikke rulle på hinanden. Vi må derfor ændre den nærliggende værdi ω1 = R/r·ω lidt, så ω1 ikke bliver konstant. Vi vælger at sætte 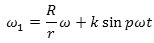Ved at vælge en ikke for stor værdi af k kan vi sørge for, at vinkelhastigheden holder sig i nærheden af den tilstræbte værdi, og ved at vælge p passende kan vi sørge for, at vinkelhastigheden i gennemsnit over en periode holder sig på den ønskede værdi. Vi får brug for at kende den vinkel q(t), som det lille tandhjul har drejet sig i tidsintervallet fra 0 til t på grund af vinkelhastigheden ω1. Man finder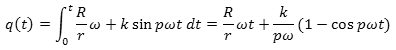

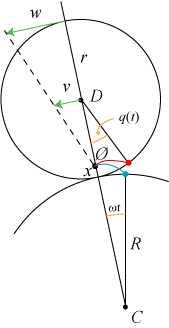
Figuren viser situationen til et tidspunkt t. v er hastigheden af den lille cirkels centrum, v = (R+r)ω. w er hastigheden af det punkt på den lille cirkel, der til tidspunktet t ligger på forlængelsen af CD, så w = (R+2r)ω+rω₁. På figuren har vi konstrueret det øjeblikkelige drejningspunkt Ø. Bevægelsen af det lille tandhjul kan altså fremkomme ved, at Ø´s banekurve i den bevægelige plan ruller på Ø´s banekurve i den faste plan.

Ved hjælp af to ensvinklede trekanter på figuren kan man opskrive en ligning til bestemmelse af den lille afstand x, der bestemmer beliggenheden af Ø. Efter lidt udregning finder man, at

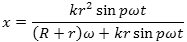
hvor x er positiv, når Ø ligger uden for den store cirkel, og negativ, når Ø ligger inde i den store cirkel.

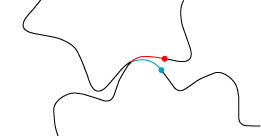
For t = 0 ligger det øjeblikkelige drejningspunkt Ø på den store cirkel lodret over C. Det sted markerer vi med et blåt punkt i den faste plan og et rødt punkt i den bevægelige plan. De to punkter kan først ses, når man drejer lidt. Figuren ovenfor viser som nævnt situationen til tidspunktet t. Det blå punkt ligger, hvor det lå før, men det røde punkt har flyttet sig på grund af den lille cirkels drejning. Punkterne er fremhævet på figuren. Vi markerer nu beliggenheden af det nye Ø i den faste plan med et blåt punkt, og samme punkt markeres i den bevægelige plan med et rødt punkt. De to punkter gemmer sig bag det sorte punkt. Hvis man gennemfører denne konstruktion for mange tætliggende værdier af t, bliver resultatet en blå kurve i den faste tandhjuls plan og en rød kurve i den bevægelige plan, og under bevægelsen ruller den røde kurve på den blå. På figuren ovenfor viser vi den del af de to kurver, der svarer til tidsintervallet fra 0 til t.

Herunder er de to kurvestykker tegnet ind på de færdige tandhjulsprofiler. Profilerne fremkommer som helhed, når man lader t variere op til 360°.

Vi vælger nu talværdier for de forskellige parametre: R = 5, r = 3, ω = 1, k = ½ og p=π/18. Så får vi, ved indsættelse i ovenstående formler, følgende udtryk for x og q(t):

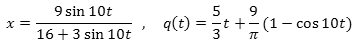
hvor vi også har skiftet vinkelmålet fra radianer til grader. Det er disse udtryk, der er brugt ved konstruktionen af tandhjulene i animationen. De er også, sammen med t = 12°, brugt på de to figurer.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.