Forside Søgning Liste

Begreberne arbejde og energi

De nævnte begreber blev først afklaret et stykke inde i 1800-tallet. Imidlertid viser Coulombs arbejde med måling af elektriske ladninger, at han omkring år 1785 havde en korrekt men begrænset viden om begreberne. Her beskriver vi, uden at gå i detaljer, den viden, som man på Coulombs må have været i besiddelse af. Vi bruger enheder, som også kan bruges i dag, nemlig følgende:

Masse måles i kg.
Afstand måles i mm.
Hastighed måles i mm/sek
Acceleration måles i mm/sek².
Kraft måles i kg·mm/sek².
Arbejde og energi måles i kg·mm²/sek².

Når vi ovenfor bruger længdeenheden mm er det fordi de flytninger Coulomb iagttog var meget små. I andre sammenhænge er det naturligt at bruge længenheden 1 meter.

Når en kraft af størrelsen K påvirker en partikel i hvile med massen m, begynder partiklen at bevæge sig i kraftens retning. Hvis partiklen T sekunder senere har bevæget sig stykket s defineres det arbejde, som kraften har udført, som kraft·vej, altså K·s. Arbejdet måles derfor som nævnt i enheden kg·mm²/sek².

På animationen nedenfor viser vi et eksempel hvor s = 150 mm og hvor T = 20 sekunder. Vi tænker os endvidere, at massen m af den blå kugle er 2 kg. Vejlængden s, accelerationen w og tidsintervallet T er forbundet med hinanden ved ligningen s = ½wT², en ligning som allerede Galilei kendte. Indsætter vi s og T i ligningen får vi, at w = 0,75 mm/sek² . Hvert sekund stiger hastigheden altså med 0,75 cm/sek, og sluthastigheden bliver derfor 20·0,75 = 15 mm/sek, sådan som det også kan aflæses af speedometret.

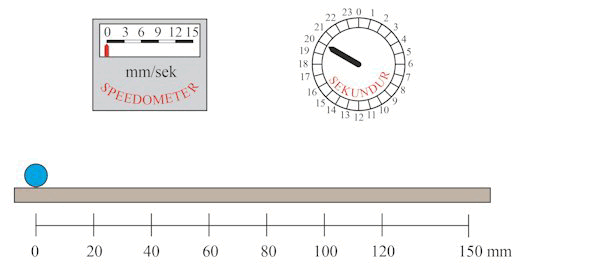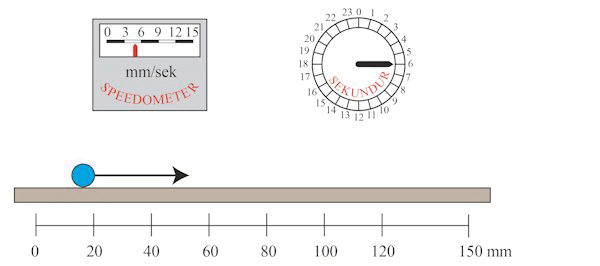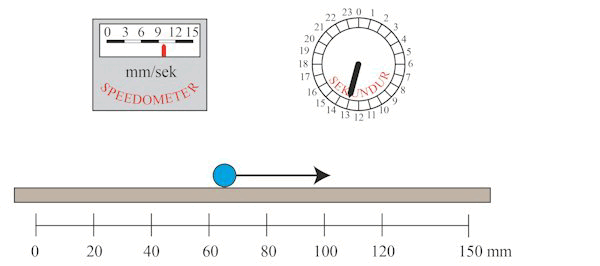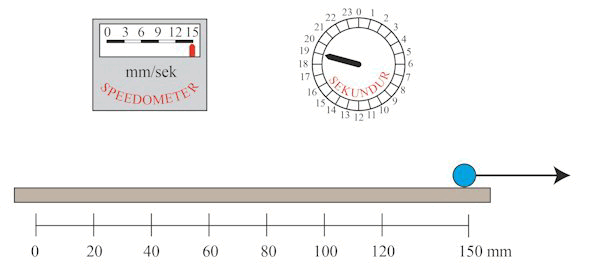
Den sorte pil viser den konstante kraft K, som den blå kugle er påvirket af. Ifølge Newtons 2. lov er K = m·w = 2·0,75 = 1,5 kg·mm/sek² .

Vi kan nu let bestemme det arbejde, som kraften K udfører når den blå kugle bevæger sig de viste 150 mm. Arbejdet er nemlig A = kraft·vej = 1,5·150 = 225 kg·mm²/sek².

2. Begrebet kinetisk energi

Vi betragter nu den samme situation som ovenfor, hvor vi ved hjælp af en konstant kraft K i tiden T udfører et arbejde af størrelsen A = Ks på partiklen med masse m. Partiklen bevæger sig med konstant acceleration w og opnår til tidspunktet T hastigheden v = wT. Nu er partiklen selv i stand til at udføre et arbejde af størrelsen A. Man siger, at partiklen har den kinetiske energi A. Den kan udtrykkes ved partiklens øjeblikkelige egenskaber:

A = K·s = mw·½wT² = ½m(wT)² = ½mv²

Formlen udtrykker, at en partikel med masse m og hastighed v kan kan udføre et arbejde af størrelsen e = ½mv². Dette udtryk bestemmer altså partiklens kinetiske energi.

Formlen gælder uanset hvordan hastigheden v er opnået. I beviset bruger vi, at hastigheden specielt kunne være opnået ved konstant acceleration.

3. Begrebet potentiel energi

Det, som vi har beskrevet ovenfor, kunne godt tænkes at foregå ude i verdensrummet. Men her på Jorden er den en anden type energi, som tit spiller en rolle, og som også bruges i praksis. For eksempel benytter den type vandhjul, som man kalder overfaldshjul, vands potentielle energi ("beliggenhedsenergi"), sådan som man kan se på billedet til højre. Lad os sige, at man løfter et legeme med masse m fra Jordens overflade og op i højden h, og lægger det der. Så har man udført et arbejde af størrelsen e = mgh, hvor g er tyngdeaccelerationen Man siger, at legemet har en potentiel energi af størrelsen e = mgh. Denne energi kan man udnytte på forskellige måder, f.eks. som nævnt i vandmøller. Størrelsen gh er den tyngdekraft, som et lod der vejer 1 kg er påvirket af. Denne tyngdekraft kaldes 1 kg*. Det er tit hensigtsmæssigt at måle kræfter i kg*.

Hvis man løfter 1 kg 1 meter opad, har man udført et arbejde. Man siger, at man har udført et arbejde på 1 kilogrammeter. Dette er en enhed for arbejde og energi, som er let forståelig, og som vi benytter når vi beskriver Joules bestemmelse af varmens mekaniske ækvivalent.

4. Bevares den samlede energi?

Allerede Huygens var klar over, at ved fuldstændig elastiske stød bevares den kinetiske energi. Han var naturligvis også klar over, at ved et stød mellem 2 ens bløde lerkugler, der bevæger sig mod hinanden med lige store hastigheder, så forsvinder den kinetiske energi fuldstændig. På animationen til venstre viser vi to fuldstændig elastiske kugler, en grøn, og en rød, der er dobbelt så tung. Hvis man regner på det kan man se, at den kinetiske energi kan omdannes til en potentiel energi af samme størrelse.

Men masser af daglige erfaringer viser, at den samlede mekaniske energi godt kan forsvinde helt. Hvor bliver den af? Det spørgsmål var Grev Rumford den første, der gav et kvalitativt svar på. Det var i 1798, der er link for oven. Men vi skal helt frem til 1843 før James Prescott Joule gav et kvantitativt svar på spørgsmålet.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.