| Forside Søgning Liste |  |
| Ind til listen: |
Joseph Blacks arbejder med varmelære
1. Blacks kalorimeter og definitionerne af varmemængde og varmefylde
I midten af 1700-tallet var konstruktionen af pålidelige termometre forholdsvis ny. Ole Rømer var først, men Fahrenheits termometre blev bedre kendt. Fahrenheit havde under et besøg hos Rømer set, hvordan Rømers konstruktion foregik. Læs om det under 1702 Rømer, der er link foroven her på siden.
I sine studier af varmelære afstod Black klogt fra spekulationer om, hvad varme er. Han gik konstruktivt til sagen med følgende definition af varmemængde: Varmemængde måles i enheden kalorie.
| 1 kalorie defineres som den varmemængde, der skal til for at opvarme 1 gram vand 1°C. |
Ordet kalorie er afledt af det latinske ord for varme, "calor".
Celciusgraden var kendt på Blacks tid, men Black brugte måske en anden vægtenhed end gram. I vores beskrivelse her bruger vi gram. Definitionen her giver kun mening, hvis der skal samme portion varme til at opvarme 1 gram vand 1°, lige meget hvad begyndelsestemperaturen er. Det kunne Black kontrollere med meget simple forsøg. Han kunne f.eks hælde ½ liter kogende vand og ½ liter vand ved 0° ned i en flaske og så røre rundt. Det viste sig at temperaturen var tæt ved 50°. Der skal altså samme varmemængde til at varme en liter vand op fra 0° til 50° som til at varme det op fra 50° til 100°. Mange forsøg af denne art bekræfter definitionens gyldighed.
Indtil Blacks tid var de grundlæggende fysiske størrelser længde, masse og tid. Det var et meget betydningsfuldt skridt for fysikkens udvikling, at Black til disse tre størrelser føjede den nye størrelse varmemængde. Omtrent samtidig med Black tilføjede Coulomb endnu en grundlæggende fysisk størrelse nemlig elektrisk ladning.
Black blev med det samme klar over, at der ved den beskrevne slags forsøg også måtte tages hensyn til temperaturændringer af den beholder, han benyttede. Black konstruerede derfor sit kalorimeter. Det blev i nogenlunde Blacks udgave brugt frem til opfindelsen af termoflasken. Vi har ikke kunnet finde nogen samtidig tegning af Blacks kalorimeter. Tegningen nedenfor viser et kalorimeter, som det jeg brugte i min skoletid omkring 1950.
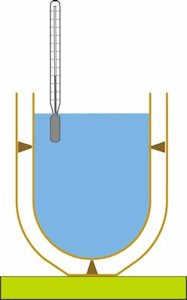 |
Kalorimetret består af to blankpolerede skåle af kobber, den ene er anbragt inde i den anden, fastholdt af nogle isolerende spidser. De var nok af kork. Rummet mellem skålene var et isolerende luftmellemrum, og
varmestråling fra den ene skål til den anden blev i vid udstrækning tilbagekastet, så der skete ingen nævneværdig varmeudveksling mellem skålene. Jeg husker apparatet som ca. 20 cm højt.
Når man bruger kalorimetret, kommer der hele tiden vand med forskellige temperaturer ned i det. Disse temperaturer forplanter sig straks til den inderste kalorimeterskål. Derfor er det nødvendigt at finde ud af, hvor stor varmemængde der bruges til at opvarme den inderste kalorimeterskål. Mere præcist definerede Black et stofs varmefylde:
Enheden for varmemængde bliver kalorie pr. gram pr. grad. - Det danske ord varmefylde er skabt af H.C.Ørsted. På engelsk hedder varmefylde specific heat. |
Nu går vi så over til at bestemme kobbers varmefylde. Vi tænker os, at stuetemperaturen er 18° og at den indre kalorimeterskål vejer 130 gram. Så hælder vi 200 g 50° varmt vand ned i skålen og rører rundt et øjeblik med en tynd pind. Resultatet bliver en temperatur på 48,5°. Vandet har så afleveret 1,5·200 = 300 kalorier til skålens 130 gram kobber, altså 300/130 = 2,31 kalorier pr gram kobber. Da temperaturstigningen af kobberet er 48,5-18 = 30,5 bliver kobbers varmefylde 2,31/30,5 = 0,08 kal/gram·grad. Mere korrekt er kobbers varmefylde 0,091 kal/gram·grad.
Når man på denne måde har bestemt kobbers varmefylde, kan man bruge kalorimetret til at bestemme andre stoffers varmefylde. F.eks. kan man bestemme varmefylden af sølv således:
Nede i kalorimetret stiller man en sølvplade på ca 1×5×5 cm; den vejer 250 gram. Begyndelsestemperaturen er 18°. Så hælder man 200 gram 50° varmt vand ned i kalorimetret og lægger et låg af kork på, så varmen får tid til at brede sig ind i sølvet. Sluttemperaturen bliver 46,39°.
Så har vandet afleveret 200·(50 - 46,39) = 722 kalorier. Den varmemængde, som kobberet har modtaget,
er varmefylde·vægt·temperaturstigning = 0,09·130·(46,39 - 18) = 332 kalorier.
Den varmemængde, som sølvet har modtaget, er 722 - 332 = 390 kalorier. Det bliver 390/250 = 1,56 kalorier pr. gram,
og heraf fås, at det bliver 156/(46,39 - 18) = 0,055 kalorier pr. gram pr. grad.
Varmefylden af sølv er altså 0,055 kalorier pr. gram pr. grad.
Kalorimetret kan også bruges til bestemmelse af varmefylden af væsker. F.eks. kan varmefylden af ren sprit findes således:
Man hælder 200 gram sprit i kalorimetret ved begyndelsestemperaturen 18°. Så lægger man en kobberplade, der vejer 150 gram og som er opvarmet til 45°, ned i spritten. Sluttemperaturen viser sig at blive
20,6°.
Så har kobberpladen afleveret 0,091·150·24,4 = 329 kalorier.
Og så har kalorimetret modtaget 0,091·130·2,6 = 30,8 kalorier.
Derfor har spritten modtaget 329 - 30,8 = 298 kalorier.
Det bliver 298/200 = 1,49 kalorier pr. gram og 1,49/2,6 = 0,57 kalorier pr. gram pr. grad.
Varmefylden af sprit er altså 0,57 kal/gram·grad .
Kalorimetret kan også med noget besvær bruges til at bestemme varmefylden for luftarter. Det gør man ved langsomt at lede en kendt masse opvarmet luft gennem gennem et spiralsnoet kobberrør, som er nedsænket i vand i kalorimetret.
Vi afslutter dette afsnit med en lille tabel over varmefylder:
|
|
|
Som man kan se af tabellen afhænger en luftarts varmefylde af, om opvarmningen sker under konstant tryk eller konstant rumfang.
Vands store varmefylde spiller en afgørende rolle for klimaet. Når sommersolen har lunet vandet i de danske farvande, og når Solen om efteråret står lavt på himlen, så bliver det ikke så koldt, som man kunne tro. Det lune vand indeholder store varmemængder, og det holder luften over Danmark varm, på trods af den lavtstående sol. Om foråret er det anderledes. Her står Solen allerede i april og maj højt på himlen, men luften forbliver kølig, fordi det på grund af vands store varmefylde tager lang tid for Solen at opvarme det kolde vintervand.
Man kan også sige det på den måde, at vands store varmefylde er årsag til, at sankthansaften ikke ligger midt i sommerferien!
|
|
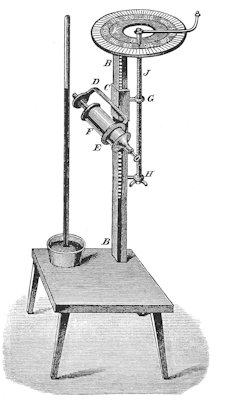
Når man skal arbejde med et kalorimeter spiller nøjagtigheden af temperaturmåling tit en afgørende rolle. På billedet til venstre viser vi et apparat, som Black benyttede ved sin temperaturmålinger. Apparatet
kaldes et katetometer.
Det er konstrueret af Stephan Gray; han er i dag mest kendt for sit arbejde med elektricitetslære.
Katetometret bruges til måling af højdeforskelle i kviksølvsøjler i termometre og barometre. På billedet er det er barometer, man aflæser. Katetometret har en faststående solid lodret søjle BB. C er en lille kasse med et firkantet lodret hul igennem; hullet passer til BB. På siden af kassen er der på en lille stang fastgjort en møtrik G, og gennem møtrikken er der skruet en gevindstang HJ. Stangen ender forneden i et fast punkt H, og for oven er der et håndsving, der peger ud til højre. Den inddelte skive for oven bæres af stangen BB, så den roterer og løftes ikke, når håndsvinget drejes. Derimod kan kassen C løftes og sænkes ved drejning af håndsvinget. Lige under håndsvinget er der fastgjort en lille vandret viser; den drejer rundt sammen med håndsvinget. Yderst er skiven inddelt i grader, men cirkelringen inden for den må, såvidt jeg kan se, dreje med viseren rundt og den må lige omkring viseren være inddelt, sådan som en nonius bør være, se link ovenfor. Vores tegning, som stammer fra LaCour, er uklar på dette punkt. Jeg tror selv, at min fortolkning er korrekt. På kassen C er der fastgjort et vandret mikroskop FE. Mens man i mikroskopet kigger på toppen af kviksølvsøjlen, kan man ved at dreje på håndtaget for oven finde det gradtal, som viseren peger på, og så kan man ved at aflæse nonius få en tilfredsstillende nøjagtighed. |
2. Blacks bestemmelse af smeltevarme
På Blacks tid var det den almindelige opfattelse, at når et stykke is først var opvarmet til smeltepunktet ved 0°C, så skulle der ikke nævneværdig varme til at smelte isen. Black mente, at simple iagttagelser viste, at dette synspunkt var forkert. Som et eksempel nævner han, at når man tager et stykke is fra hård frost ind i varmen, så vil den ret hurtigt blive opvarmet til smeltepunktet ved 0°, men derefter går der lang tid før isen er smeltet tilvand. Og det vand har stadig temperaturen 0°. Der kræves altså en betydelig mængde varme, når et stykke is skal smeltes, selv om temperaturen ikke ændres.
Argumentet ovenfor er overbevisende, men Black udtænkte et meget enkelt forsøg, der ændrede resultatet fra at være kvalitativt til at være kvantitativt.(Dvs. fra at være principielt til at være baseret på tal.)
|
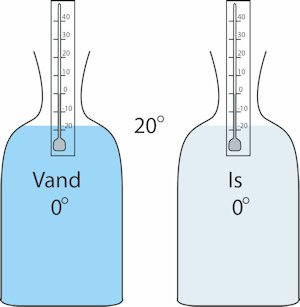
Formålet med forsøget er at bestemme den varmemængde, der kan omdanne 1 gram is ved 0°C til 1 gram vand ved 0°C. Denne varmemængde kaldes isens smeltevarme. På billedet til højre viser vi forsøgsopstillingen. Den består af to ens glasflasker. Den
ene er fyldt med 1 liter vand ved temperaturen 0°C, og den anden er fyldt til samme niveau med is også ved 0°C. Flaskerne står i et rum, hvor temperaturen er 20°. Black finder det så indlysende, at så længe
flaskernes temperaturer er næsten ens vil der hele tiden trænge samme varmemængde ind i de to flasker.
Så kommer resultatet: På 15 minutter blev vandet i vandflasken opvarmet til 4°C, men det tog 5 timer, altså 20 gange så lang tid, før al isen i den anden flaske var smeltet. Temperaturen i den flaske er stadig 0°. Det kvalitative resultat er, at der kan tilføres varme til is, uden at temperaturen stiger. Men der kan også udledes et kvantitativt resultat af forsøget: Den varmemængde, der trænger ind i vandflasken, er 4000 kalorier. Der går altså 20·4000 kalorier til at smelte et kilo is, og derfor går der 20·4 = 80 kalorier til at smelte et gram is ved temperaturen 0°. Man siger, at
| 
|
På samme måde opstår der varme, man kunne kalde det størkningsvarmen, når vand, der er afkølet til 0°, fryser til is ved 0°. I vore dage vil man sige, at størkningsvarmen må være lig smeltevarmen, fordi
varmeenergien er konstant. Sådan kunne man ikke tænke på Blacks tid, men Black kunne med noget besvær kontrollere det med sit kalorimeter.
| Opgave 23 Beskriv et kalorimeterforsøg til bestemmelse af størkningsvarmen for vand. |
3. Blacks bestemmelse af fordampningsvarme og fortætningsvarme
Ligesom Black havde undersøgt overgangen fra fast stof til væske, ville han også undersøge, hvad der sker, når vand ved kogning bliver til vanddamp. Allerede omkring 1681 havde Papin med sin gryde haft mulighd for at undersøge hvad der sker med vand ved kogning. Han kunne. med sin sikkerhedsventil konstatere, at kogepunktet vokser med stigende tryk, og han vidste også godt, at ved konstant tryk ændrer temperaturen sig ikke under kogningen. Han havde dog ikke adgang til gode termometre, så længere kom han ikke. Læs om Papins gryde under 1681 Papin, der er link for oven her.
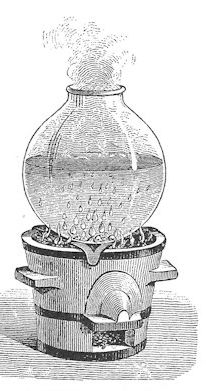 | Det første Black gjorde, var omhyggeligt at iagttage hvad der sker, når koldt vand opvarmes til kogepunktet. Han sætter en glasbeholder med vand på en rist over nogle glødende trækul. Lige til at begynde med sker der ingenting, men lang tid inden kogepunktet er nået stiger der små bobler op nede i vandet, sådan som man kan se på billedet til venstre. Boblerne indeholder luft, der har været opløst i vandet. Jeg ved ikke, om Black vidste dette. Samtidig kommer der en sitrende lyd fra vandet. Efterhånden som vandet nærmer sig kogepunktet, erstattes den sitrende lyd af en boblende lyd, der vedvarer, når kogepunktet er nået. Som vist til højre stiger der bobler op til overfladen, der bliver meget urolig. Under kogningen ændres temperaturen ikke, selv om der stadig tilføres varme til vandet. | 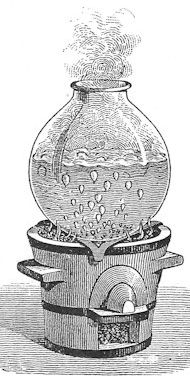 |
Før Black forklarede man dette ved at hævde, at det kun er vandet på bunden af beholderen, der har nået kogepunktet. Vandet højere oppe har ved begyndelsen af kogningen ikke nået kogepunktet. Når alt vandet har nået kogepunktet skal der kun en ganske lille damptilførsel til at omdanne alt vandet til damp. Denne forklaring tilfredsstillede ikke Black. LaCour citerer Black for at skrive følgende:
| Jeg kan let vise, at selv om vandet er opvarmet til en sådan temperatur, at den mindste temperaturforhøjelse vil gøre vandet til damp, så vil dampdannelsen dog kræve en stor mængde varme. Var det ikke således, da ville
hele vandmassen eksplodere (dvs i et øjeblik blive til damp) med en kraft, der kunne sammenlignes med krudtets. Men jeg kan vise, at den nødvendige store varmemængde går jævnt ind i dampen, mens den danner sig, uden at den dog
bliver opvarmet så meget, at det kan iagttages på et termometer. -
Sættes en kedel vand over ilden, da går varmen fra det første øjeblik og til kogningen begynder, hurtigt gennem kedlen over i vandet.
Måske iagttager vi, at vandet i løbet af 5 minutter opvarmes 11°C. Nu har man lagt mærke til, at varmens overgang fra et legeme til et andet sker i forhold til forskellen i temperatur, når de øvrige omstændigheder bliver fuldstændig uforandrede. Derfor kan vi i dette tilfælde, da vandets temperatur under kogning ikke stiger kendeligt (i forhold til ildens temperatur) have lov til at slutte, at varmen (under kogningen) må strømme over i vandet i omtrent samme mængde som før kogningen. Dette fører ikke til noget galt, for jeg har ofte selv set, at når vandet i de sidste 5 minutter før kogningen steg 11°C, så tog det 40 minutter at opvarme vandet til 88°C. Var nu den almindelige mening (om kogningen) rigtig, da er det klart, at hele vandmassen vil blive til damp i nogle minutter, en umådelig udvidelse vil finde sted, og den ville være kraftig nok til at sprænge huset i luften. - Jeg kan ikke huske andet, end at jeg altid har haft en uklar forestilling om, at den gængse opfattelse af fordampningsfænomenet var uforenelig med kendsgerningerne; og jeg tænker mig, at det er gået de allerfleste ligeså, når de har lagt mærke til kogning i en kedel eller i en pande. Men denne mistanke virkede ikke på mig med tilstrækkelig styrke, før jeg havde gjort mine forsøg over isens smeltning. |
Der er flere uklarheder i dette citat. LaCour skriver ikke, hvor han har citatet fra, og jeg gætter på at det stammer fra en af de mange tilhørere, som mødte frem til Blacks forelæsninger.
Black mente, at selv om vand er opvarmet til kogepunktet på 100°C, så skal det tilføres en betydelig varmemængde, før alt vandet er fordampet. Og når dampen forlader vandet, er dens temperatur 100°C. Varmen må altså på en eller anden møde være bundet i dampen, selv om temperaturen ikke er steget. Black definerede så vands fordampningsvarme:
| Vands fordampningsvarme er den varmemængde der skal til, for at omdanne 1 gram vand ved 100°C til damp ved samme temperatur |
Black prøvede at bestemme fordampningsvarmen på følgende måde: Han bragte vand i kog over en jævn ild. Så vil der i lige lange tider blive udviklet lige meget damp. Så målte han den tid der gik med at få vandet op på kogepunktet, og derefter den tid der gik, før alt vandet var fordampet. På den baggrund kunne fordampningsvarmen beregnes. Vi illustrerer metoden med et eksempel:
Mens ilden holdes konstant varmes 1 kg vand op fra 10°C til kogepunktet på 15 minutter. Dernæst går der 90 minutter før alt vandet er fordampet. På 15 minutter går der altså 90 kalorier pr gram vand for at opvarme det til kogepunktet. I de 90 minutter, som kogningen varer, går der 6·90 = 540 kalorier pr. gram vand til at omdanne det 100 grader varme vand til damp ved 100°. Vands fordampningsvarme er altså 540 kalorier pr.gram.
Black nåede ikke selv til dette resultat. Hovedårsagen til det er, at det er vanskeligt at iagttage et præcist tidspunkt for kogningens begyndelse.
|
Når vanddamp rammer et koldt stykke metal, omdannes dampen til vand, der sætter sig som dug på metallet. Hermed bliver metallet opvarmet. Den varme, der går over i metallet, kaldte Black fortætningsvarmen. Mere præcist defineres
vanddamps fortætningsvarme således:
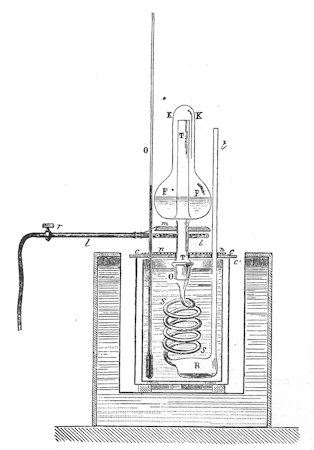
Som nævnt ovenfor kan luftarters varmefylde måles ved at man leder luftarten gennem et spiralsnoet kobberrør, der står i et kalorimeter. Den samme ide kan bruges ved måling af fortæningsvarmen for vanddamp. På figuren til venstre viser vi hvordan det kan foregå. Opstillingen her må være meget senere end Black, der bruges nemlig gas til opvarmningen. Men princippet er det samme, som hvis man brugte trækul. Gassen kommer ind fra venstre, og gasblusset under flasken FF holder vandet i flasken i kog. Røret TT kommer op i flasken nedefra, og på et tidspunkt skubbes flasken og røret nedad, så den situation, der er vist på figuren opstår. Der strømmer nu 100° varm damp ned gennem det spiralsnoede rør, og da der er koldt vand i kalorimetret fortættes dampen til vand, der samler sig nede i beholderen B. Det tynde lodrette rør til højre for flasken er åbent foroven, så der er atmosfærens tryk i hele systemet. |
Hvis man så har styr på alle de variable, kan vands fortætningsvarme udregnes. Vi giver et eksempel:
I et kalorimeter er der 200 gram vand ved 15°C. Nede i beholderen B fortættes der 2,5 gram vand. Temperaturen i kalorimetret er steget til 23°; stigningen er altså 8°.
Vandet i kalorimetret har altså modtaget 8·200 = 1600 kalorier.
Vandet i B er afkølet fra 100° til 23°, altså 77°
Vandet i B har altså afgivet 2,5·77 = 192,5 kalorier.
Ved fortætningen er der altså opstået 1600 - 192,5 = 1407,5 kalorier, dvs. 1407,5/2,5 = 563 kalorier pr. gram
Ifølge dette forsøg er fortætningsvarmem altså 563 kalorier pr gram. Det rigtige tal er 536 kalorier pr. gram.
For ikke at komplicere sagen har vi her set bort fra temperaturændringen i kalorimetret og i kobberet i spiralrøret.
4.Konklusion
Vores viden om Blacks arbejder er begrænset af det forhold, at han publicerede meget lidt. Vores hovedkilde er LaCour, og vi gætter på at LaCour havde sin viden om Black fra de publikationer om Black, som nogle af tilhørerne til hans forelæsninger senere offentliggjorde. Ikke desto mindre mener vi, at Blacks resultater er meget betydningsfulde. Kalorien er en enhed for det, vi i dag kalder energi, og Black opdagede en række processer, hvor varmeenegien bevaredes. Det generelle begreb energi blev først klarlagt i midten af 1800 - tallet.
Black var en nær ven af James Watt, og de må have talt meget med hinanden om varme og damp. Det er dog uklart, om Blacks teoretiske resultater spillede er rolle for Watts arbejde med dampmaskiner.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |