Forside Søgning Liste

For bedre at kunne forklare Bradleys opdagelse af aberrationen starter vi med en animation. Den gule kugle bevæger sig nedad med konstant fart c, og det brune rør bevæger sig mod højre med en anden konstant fart r. Opgaven er at vælge en sådan hældning af det brune rør, at kuglen frit kan bevæge sig ned gennem røret, sådan som det er lykkedes på animationen.

Lad os et øjeblik opfatte røret som en kikkert, som man kigger op igennem, og som bevæges mod højre. Og lad os tænke os, at kuglen er et lysglimt, der kommer oppefra. Hvis man vil se lysglimtet midt i kikkerten, så skal man ikke rette kikkerten mod det sted, som lyset kommer fra. Man skal rette røret skråt fremad i bevægelsesretningen. Lysets retning flyttes altså fremad i kikkertens bevægelsesretning, det ser ud som om lyskilden flyttes et stykke fremad i bevægelsesretningen.

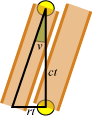Lad os sige, at kuglen er t sekunder om at gennemløbe røret. På figuren til venstre viser vi begge de to situationer, hvor kuglen bevæger sig ind i røret, og hvor den bevæger sig ud af røret. I disse t sekunder har kuglen bevæget sig en lodret strækning af længde ct og røret har bevæget sig strækningen rt til højre. Den grønne vinkel v er den vinkel, som røret skal danne med lodret, hvis forsøget skal lykkes. Af den viste trekant fås, at tan v = rt/ct = r/c. Hvis man kender r og c, kan man altså regne ud hvor skråt røret skal være. Eller omvendt: Hvis man ved, hvor hurtigt røret bevæger sig, og ved forsøg finder den rigtige rørhældning v, så kan man regne ud, hvor hurtigt kuglen bevæger sig.

Nu går vi over til at beskrive Bradleys opdagelse, der blev publiceret i 1728. I årene fra 1669 til 1680 opdagede forskellige astronomer, at visse stjerner tilsyneladende flyttede sig en lille smule frem og tilbage. På den tid ledte man ivrigt efter stjerners parallakse, og nogen troede, at det var den, man endelig havde fat i. For overskuelighedens skyld kigger vi nu på en stjerne tæt på Ekliptikas Nordpol.

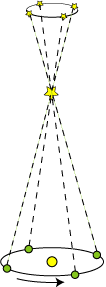
Aberrationen	Parallaksen
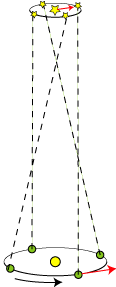Den stjerne, vi kigger på, er i korrekt position vist lidt større end de andre stjerner. Men det er ikke der, man ser den. Bradley og Molineux fandt nemlig ud af, at stjernen i løbet af et år bevægede sig rundt i en lille cirkel. Stjernen bevægede sig i takt med Jorden, men stjernen var hele tiden ¼ omgang forud for Jorden, sådan som det er vist med de punkterede linier, og sådan som det er vist herunder, set højt oppefra.	På Bradleys tid havde man endnu ikke målt nogen parallakse. Men man vidste godt, at det var fordi målenøjagtigheden ikke var stor nok. Man vidste også at parallaksebevægelsen foregår, som det er vist på figuren ovenfor. Stjernen er i korrekt position tegnet stor, og Jordens bevægelse om Solen bevirker, at sigtelinien fra os til stjernen og videre ud mod de fjerne nabostjerner hele tiden skifter. Det ser ud som om stjernen i årets løb bevæger sig rundt på en lille cirkel, sådan som det er vist med de punkterede linier. Man ser, at stjernen i sin bevægelse er en halv omgang forskudt i forhold til Jorden, sådan som det også er vist herunder, set højt oppefra.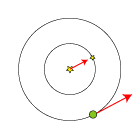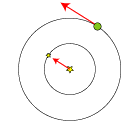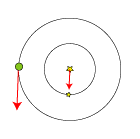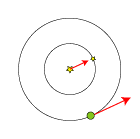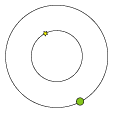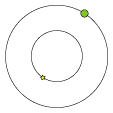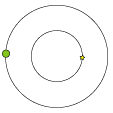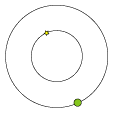

På baggrund af overvejelserne ovenfor kunne man konkludere, at det ikke var stjernens parallaksebevægelse, som Bradley og Molineux var igang med at undersøge, stjernens og Jordens indbyrdes stilling passer ikke med parallakseteorien.

På den anden side var det klart, at det iagttagne fænomen måtte skyldes Jordens bevægelse, ellers ville perioden jo ikke være nøjagtigt et år. Og så var det, at Bradley kom i tanke om det fænomen, som vi startede med at beskrive. Vi så, at hvis en kikkert bevæger sig, og man vil se en stjerne, så skal man ikke rette kikkerten direkte mod stjernen, kikkerten skal drejes lidt fremad i sin egen bevægelsesretning. Og vores kikkerter bevæger sig jo med Jorden rundt om Solen. Og se så på figuren ovenfor, hvor fint det passer. Den nederste røde pil angiver Jordens - og dermed kikkertens - bevægelsesretning og den øverste angiver stjernens flytning. Og de to er parallelle, hele vejen rundt. Hermed havde Bradley givet en kvalitativ forklaring på stjernens (tilsyneladende) bevægelse.

Men passer det nu også kvantitativt, har den lille cirkel en beregnbar størrelse? Observationerne viste, at den lille cirkel havde en vinkeldiameter på 40". 40 buesekunder er 1/90 af en grad, dvs 1/45 af Månens diameter, der jo er ½°. Der er altså plads til 45 af de små cirkler tværs over Månen. Nu er vi så i den situation, som vi startede med at beskrive:

I forhold til den forventede position skal kikkerten drejes 20" fremad, så den grønne vinkel v på figuren er 20". Og rørets, dvs kikkertens hastighed r er Jordens hastighed i sin bane om Solen. Jorden er R = 150 milloner kilometer fra Solen, så Jordbanens omkreds O er

Så langt bevæger Jorden sig på et år. Hvis man vil have bevægelsen på et sekund skal man dividere med antallet af sekunder i et år, altså med

Resultatet er, at Jorden i sin bane om Solen bevæger sig 30 km/sek, og det er så hastigheden r i den øverste formel. Og så skal vi til sidst bruge formlen på formen

hvor det midterste lighedstegn gælder, når vinklen v er målt i radianer i stedet for grader. Gradmålet for v bliver 20/(60·60) = 1/180 = 0,0055. Radianmålet for v bliver derfor 0,0055·2π/360 = 0,0001. Slutresultatet bliver derfor, at

Her bør det give et sæt i læseren: Bradley har fundet lysets hastighed ved at måle diameteren af de små aberrationscirkler, som stjernerne synes at bevæge sig i. Det har nok også givet et sæt i Bradley: Rømer havde jo allerede i 1676 fundet lysets hastighed ved at studere jupitermånernes bevægelser, og der var tilfredsstillende overensstemmelse mellem resultaterne. Når man når til samme resultat på to så forskellige måder, så er der virkelig grund til at tro på det hele. Og samtidig er Bradleys resultater vedrørende aberrationen det først konkrete bevis for, at Jorden faktisk går rundt om Solen. Det er en milepæl i fysikkens historie.

Burde man egentlig ikke tage hensyn til Jordens daglige rotation? Nej, for den hastighed et punkt på Ækvator får på grund af den daglige rotation er 40.000/(24·60·60) = ½ km/sek og det er jo forsvindende i forhold til de 30 km/sek, som vi fandt ovenfor. De 40.000 km er længden af Ækvator, sådan var meteren oprindelig defineret.

Ovenfor har vi ladet som om Bradley vidste, at afstanden mellem Solen og Jorden er 150 millioner km. Det er ikke helt sandt. Det bedste bud på den afstand, som man kendte på Bradleys tid, var 138 millioner km. Det skyldtes Giovanni Domenico Cassini (1625 - 1712). Men Bradleys måling af aberrationscirklens diameter var særdeles god. Han fandt som nævnt 40", og i dag siger vi 41". Kvaliteten af Bradleys målinger kan også måles på en anden måde: Bradley gennemførte også ovenstående udregninger med den ændring, at han benyttede jordbanens radius som længdeenhed. Så bliver omkredsen O = 2π og udregningerne giver da som resultat, at lysets hastighed er c = 0,002 jordbaneradier/sek. En jordbaneradius gennemløbes derfor på 500 sekunder eller 8,4 minutter. Det rigtige resultat er at det tager sollyset 8,3 minutter at nå Jorden. Bradleys resultat er faktisk meget præcist!

For fuldstændighedens skyld skal vi nævne, at det kun er stjerner nær Ekliptikas poler, der har næsten cirkelformede aberrationsbevægelser. Længere væk fra polerne bliver bevægelserne elliptiske, og helt nede i Ekliptikas plan bliver de frem- og tibagegående.

Ud over aberrationen fandt Bradley at præcessionsbevægelsen af jordaksen er overlejret af en mindre vibration, som kaldes nutationen. Den har en periode på 18,6 år og skyldes Månens bevægelse.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.