| Forside Søgning Liste |  |
| Ind til listen: |
Henry Cavendishs bestemmelse af Jordens gennemsnitlige vægtfylde
1. Indledning
Kilden til nedenstående beskrivelse af Henry Cavendishs bestemmelse af Jordens vægt er Cavendishs egen artikel. Titlen er:
Experiments to determine the Density of the Earth. By
Henry Cavendish, Esq. F.R.S. and A.S.
Det er siderne fra 469 til 526 i Royal Societys publikation for 1798. Cavendish fremlagde artiklen i et foredrag den 21.juni 1798. Artiklen er tilgængelig på Google Scholar. Formålet med beskrivelsen her er dels at beskrive det apparat, som Cavendish brugte, og dernæst at gennemgå den metode, som Cavendish brugte til at bestemme Jordens vægt. Artiklen indeholder herudover en mængde detaljer, som vi ikke vil beskæftige os med her.
I sine udregninger bruger Cavendish kun få enkle formler. De fleste af hans udsagn er af typen A forholder sig til B ligesom C til D. I de fleste af disse tilfælde vælger vi her at skrive formler, som vi i vore dage synes er lettere at læse. Men selve Cavendishs tankegang er der ikke ændret på her.
2. Beskrivelse af det apparat, som Cavendish brugte.
Cavendishs apparat minder om den snovægt som Charles Coulomb benyttede omkring 1785, men de to fysikere kendte vist ikke hinandens arbejder.
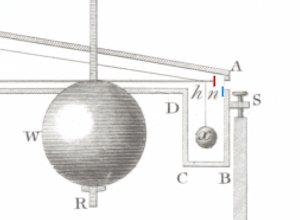
| På billedet til højre viser vi, hvordan apparatet var indrettet. Det står i et værelse, der er ca. 3 meter bredt. Gulvet er meget stabilt. Apparatet består først og fremmest af to små kugler af bly, der hver vejer 725 gram, og som har en diameter på 5 cm. De to kugler hænger under enderne af en 73,3 tommer (180 cm) lang, meget let vægtstang af træ. Stangen er ophængt i en lodret tynd tråd af messing. For oven er tråden fastgjort i den vandrette stang, som starter for oven til højre. Ved at dreje på stangen udefra kan man opnå, at når tråden ikke er snoet, hænger stangen midt i mahognikassen, som man kan se på billedet nedenfor. Tråden er forneden sat fast på tre andre tråde, to som sidder fast i stangens ender, og en kort, som støtter stangen i midten. Det bevirker, at stangen hele tiden er vandret. | 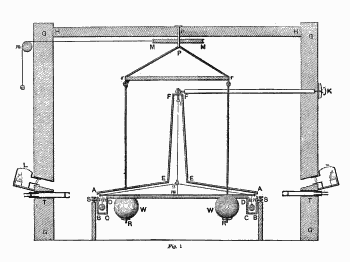 |
Der er også ophængt to store vægte af bly. Som man kan se hænger de i en vandret stang, som man kan dreje udefra ved at trække i en snor, hvis to ender kommer ud af rummet for oven til venstre. Hver af vægtene
vejer 2439000 grains, dvs 158,042 kg. En sfærisk fod er rumfanget af en kugle med radius ½ fod, som er 15,26 cm. Så 1 sfærisk fod vand
vejer
Når vi i det følgende bruger ordene kugle, vægt og stang refererer vi til de tilsvarende dele af Cavendishs apparat.
Ideen er nu, at man først drejer de store vægte langt væk fra de små, og venter på, at de små kugler falder til ro. Dernæst drejer man de store kugler, så de er så nær ved de små, som de kan komme. Så vil Newtons tiltrækningskraft på de små kugler dreje vægtstangen en lille bitte smule, og ved at måle denne drejningsvinkels størrelse kan man så udregne tiltrækningskraftens størrelse.
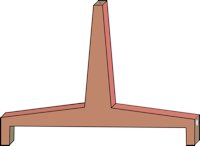 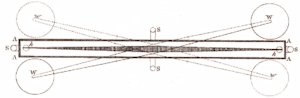
| For at beskytte de følsomme bevægelige dele mod strømninger i luften er de indesluttede i en meget tæt trækasse, som vi viser til venstre. Trækassen er lavet af mahogni, og den er meget stabil. Inde i trækassen hænger de to blykugler i korte, lodrette snore, der er fastgjort i enderne af stangen. Neden under viser vi et tværsnit af kassen, i højde med vægtstangen. Stangen kan fra midterstillingen kun dreje sig ca. 2° væk fra midterstillingen uden at støde på trækassen. Mere er der ikke behov for, fordi snoningskræfterne fra tråden er meget svage. (Cavendish taler overalt om kræfter hvor vi ville benytte drejningsmomenter.) Ideen er nu, at hvis man drejer stangen lidt væk fra ligevægtsstillingen, så bliver tråden snoet lidt, og så påvirker tråden stangen med et drejningsmoment, der er proportionalt med drejningsvinklen, og som er rettet tilbage mod ligevægtsstillingen. |
| På billedet til højre viser vi den situation, hvor en af de store vægte de er drejet så tæt på kassen, som de kan komme. Som man kan se, er linjestykket, der forbinder centret i en lille kugle med centret i en stor vægt, ikke vinkelret på stangen i dens ligevægtsstilling. Det er en konstruktionsfejl, erkender Cavendish. Fejlen gør, at virkningen af tiltrækningskraften er en smule mindre, end den ville have været, hvis den stang, der bærer vægtene, havde været en smule længere. Cavendish beregner formindskelsesfaktoren til 0,9779, vi viser hans udregning her. | 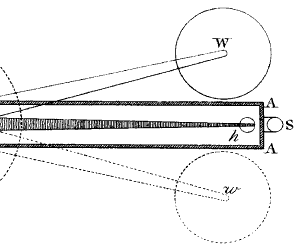 |
 | Der er to små huller i trækassen, et i hver ende. Man kan se det ene hul på billedet af trækassen. Hullerne bliver belyst af de lamper, som man kan se uden for den tykke væg på billedet øverst. Hullet foran lampen er lukket med en linse, der samler lyset på hullet i trækassen. Man kan se ind i hullet i trækassen gennem et teleskop, T på den øverste figur. På billedet til venstre viser vi, hvad man kan se. Det er to små plader af elfenben. Den ene plade, som vi kalder den blå, sidder fast på indersiden af trækassen på det sted der er vist med blåt på figuren. Beliggenheden af den anden plade, som vi kalder rød, er vist med rødt. Den plade sidder fast på enden af vægtstangen. |
| Billedet til højre viser, hvad man kan få at se gennem et teleskop. Nederst ses den fastsiddende blå plade. I den er der lavet 31 lodrette ridser. I det følgende kalder vi disse nummererede
ridser for inddelinger
Afstanden mellem to naboinddelinger er 1/20 tomme dvs 0,25 mm.
Oven over den blå skala ses den røde. Den bevæger sig frem og tilbage, når vægtstangen drejer. Den røde skala virker som en nonius, som du måske kender fra en skydelære, der er link for oven.
Cavendishs inddeling er nu lidt speciel. Afstanden mellem de to yderste ridser på den røde plade er som 4 afstande på den blå, men den er delt i 5 dele, så afstanden mellem to naboridser på den røde plade er 0,2 mm.
På figuren kan man se at den røde 0-streg peger lidt over 7 inddelinger, men da den røde streg efter tre mellemrum står nøjagtigt over 10, er den korrekte aflæsning 7,6. Hvis du synes, at det er svært, så læs
vores beskrivelse af nonius, som her måske burde kaldes quartius. Resultatet er, at aflæsningen kan foregå med en nøjagtighed på 0,05 mm.
Afstanden mellem to naboridser er som nævnt 0,05 tomme. Fra skalaen er der 38,3 tommer ind til midten af stangen. Derfor skal stangen dreje sig en vinkel på 0,05/38,3 = 1/766 radianer, hvis den røde skala skal flytte sig 1 inddeling i forhold til den blå. | 
|
3. Beskrivelse den metode Cavendish brugte til bestemmelse af Jordens gennemsnitlige vægtfylde
Overraskende nok indleder Cavendish sin beskrivelse af, hvordan beregningen af Jordens vægtfylde finder sted med at sammenligne de svingninger, som vægtstangen i hans apparat udfører, med svingninger af et pendul. Det pendul, som Cavendish benytter har en længde, der er halvdelen af vægtstangens, altså 36,5 tommer. Tidens viden om penduler stammer helt tilbage fra Huygens, der er link for oven. Det vigtigste resultat, som Huygens fandt i 1656, var at svingningstiden T for et pendul med længden r er
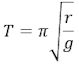
Her betyder g tyngdeaccelerationen. Cavendish definerer svingningstiden som den tid der går fra en yderstilling til den modsatte, hvor man i vore dage definerer svingningstiden som tiden fra en yderstilling til den næste i samme retning. I det følgende bruger vi Cavendishs definition, så et sekundpendul, er et som siger en lyd hvert sekund, nemlig når det er i en yderstilling. Længden af et sekundpendul er 39,14 tommer, hvor en tomme er 2,54 cm. Det følger af Huygens formel, at et pendul med længden 36,5 tommer har en svingningstid T på
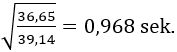
I vores omtale af drejningsmoment, der er link for oven, betragter vi et legeme kan dreje sig om en akse og har inertimoment I. Vi tænker os, at dette legeme er påvirket af et drejningsmoment D = k·A, der er proportionalt med drejningsvinklen A, og som er rettet ind mod ligevægtsstillingen. k er altså drejningsmomentet når drejningen er 1 radian. Som nævnt er svingningstiden for sådan et legeme
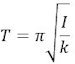
Jeg ved ikke, om Cavendish har kender denne formel, men her i vores fortolkning er det nærliggende at bruge formlen.
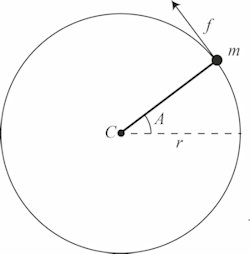 | 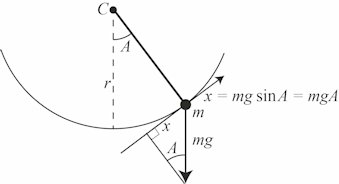 |
| Ovenfor viser vi Cavendishs vægtstang set fra oven, så det foregår i en vandret plan. Vi betragter kun den ene halvdel af vægtstangen, der altså har samme længde, r = 36,9 tommer, som pendulet til venstre. f er den kraft i tangentens retning, der kan holde vægtstangen i ligevægt, når den er drejet vinklen A væk fra ligevægtsstillingen. Kraften f er proportional med drejningsvinklen A, f = y·A. Jo stivere tråden er, jo større bliver y. Vi vælger nu en tråd med en sådan stivhed, at y = mg. Så bliver f = mgA, og drejningsmomentet bliver mgrA. | Ovenfor viser vi et pendul med længden r = 36,5 tommer og med vægten m. Det foregår altså i en lodret plan. På figuren kan man se, at en kraft på tangenten, der kan holde pendulet i ligevægt, når det danner vinklen A med lodret er x = mgA, og det drejningsmoment som kraften påvirker pendulet med bliver mgrA. |
Jeg tror, at Cavendish tænkte sig af kraften f opstår på den måde at en snor går fra m i tangentens retning hen til et hjul og videre nedad til en masse af størrelsen m.
Formlen ovenfor gælder i begge tilfælde, og da både inertimomentet og drejningsmomentet k er det samme i begge tilfælde, følger det af formlen, at svingningstiderne også er ens.
Cavendish har fundet at svingningstiden for vægtstangen er 0,968 sekunder når det moment, der kan dreje stangen 1 radian er mgr.
Cavendish bruger ikke ordet drejningsmoment, men hans argumenter er korrekte alligevel. Det har været meget tidskrævende for mig at oversætte Cavendishs argumenter til et moderne sprog:
Vi ønsker nu at ændre trådens stivhed sådan, at svingningstiden ændres fra 0,968 sek. til N sek. Vi har vist, at
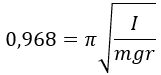
Vi multiplicerer nu på begge sider af lighedstegnet med N/0,986. Resultatet er, at
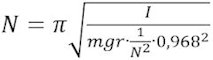
For at opnå en svingningstid på N sek. skal man altså vælge trådens k - værdi til
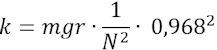
Hvis man vil dreje stangen vinklen A skal man altså bruge drejningsmomentet
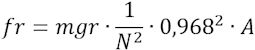 ,
,
hvor f er den kraft, der virker i afstanden r.
I vores omtale af skalaen ovenfor har vi vist, at stangen drejer sig 1/766 radianer, når aflæsningen på skalaen flytter sig 1 inddeling. Den kraft, der f1, der kan dreje stangen 1/766 radianer er
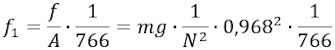
Derfor er
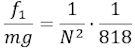
Denne formel bestemmer den snoningskraftkraft, der kan dreje vægtstangen 1 inddeling på skalaen. N er den aktuelle svingningstid, og Cavendish opdagede, at denne svingningstid måtte måles i forbindelse med hvert eksperiment.
Newton fandt ud af at den tiltrækning en homogen kugle yder på en partikel på kuglens overflade eller uden for den ikke ændres, hvis man tænker sig at kuglens masse er samlet i dens centrum. Dette er en afgørende forudsætning for de følgende overvejelser. Du kan se beviset under 1682 Newtons tiltrækningslov.
Vi går nu over til at bestemme, hvor mange gange mere Jorden trækker i en partikel med masse m på Jordens overflade, end en blyvægt trækker i en partikel med masse m når centerafstanden er 8,85 tommer. I det følgende skriver vi t i stedet for tommer, og 8,85 t er det nærmeste en kugle midt i kassen kan komme på en vægt.
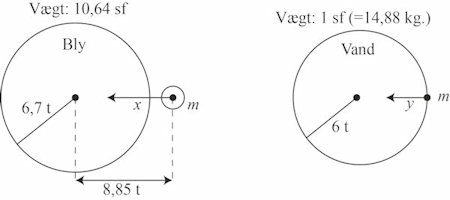
På figuren nedenfor viser vi til venstre en af blyvægtene, der som nævnt vejer 10,64 sf. sf betyder en sfærisk fod, dvs vægten af en vandkugle der er 1fod (= 12 t) i diameter. 1 sf er 14,88 kg. x er den kraft som en vægt påvirker en kugle med, når centerafstanden er 8,85 t. Til højre viser vi en vandkugle med diameter 12 t = 1 fod. y betegner den kraft med hvilken kuglen påvirker en partikel med masse m, der befinder sig på kuglens overflade. Neden under billedet af kuglerne bruger vi Newtons tiltrækningslov, hvor vægt måles i sf.
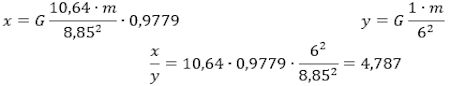
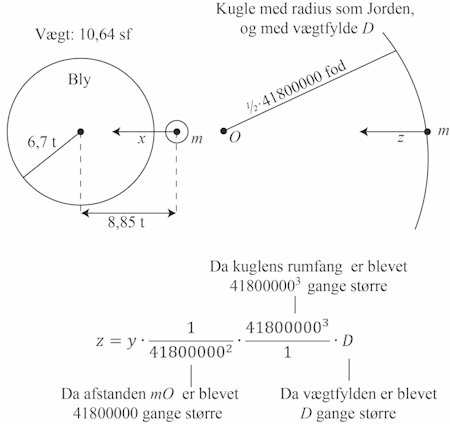
Vi erstatter nu den lille vandkugle ovenfor med en meget større kugle. Den har diameter som Jorden, nemlig 41800000 fod, og dens vægtfylde er D. På overfladen af kuglen placerer vi en partikel med masse m. Det medfører, at tiltrækningskraften y ændres til en ny tiltrækningskraft z som vi nu går over til at beregne. 6 tommer = 1 fod, og derfor gælder følgende:
Resultatet er, at z/y = 41800000·D, og heraf fås, at
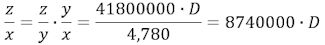
En vægts tiltrækning på en kugle i nærmest position er altså 874000·D gange mindre mindre end Jordens tiltrækning på en kugle, og det er denne meget lillle tiltrækning, som Cavendish skal måle. Kraften svarer til noget i retning af 0,015 milligram.
Vi har ovenfor vist, at den kraft, der kan flytte aflæsningen på skalaen 1 enhed er 1/818N2 gange vægten af kuglen. Derfor kan tiltrækningskraften fra en vægt flytte aflæsningen
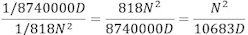 | inddelinger. |
Derfor vil det være sådan, at hvis stangen drejer sig B inddelinger når vægten flyttes fra fjern til nær, så vil
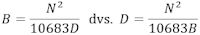
Man kan altså beregne D således: Ud fra ligevægtsstillingen sætter vi svingninger i gang ved at flytte vægtene fra fjern til nær og så måler vi svingningsstiden N og finder det antal inddelinger, som stangen har drejet sig, når svingningerne er faldet til ro. Det sidste er ikke så let:
4. Om bestemmelse af drejningsvinklen Lad os tænke os at vi har vægtene i fjern position, og at stangen er faldet til ro. Så drejer vi vægtene til nær position og den svage tiltrækningskraft fra vægtene til kuglerne for stangen til at dreje sig. Men når tiltrækningskraften har sat stangen i rotation standser den ikke i en ny ligevægtsstilling, men den begynder at svinge frem og tilbage omkring den nye ligevægtsstilling S med en svingningstid der typisk er omkring 8 minutter. Selv om udsvingende bliver mindre og mindre, kan det ikke nytte noget at vente på at de falder til ro. Dels kan det tage flere timer, men først og fremmest sker der det, at de svage kræfter, der skyldes strømninger at luften i kassen, gør det umuligt at observere S.
| På billedet til højre viser vi hvordan Cavendish valgte at bestemme den inddeling som man ser på når ligevægtsstillingen er opnået. A og B er to på hinanden følgende maksima på svingningskurven, og C er det minimum, der findes mellem de to maksima. Videre er M midtpunktet af AB og N er midtpunktet af MC. Så synes Cavendish at der må være lige meget svingning over og under den vandrette linje gennem N, og denne linje peger derfor hen mod den inddeling, som man ser mod, når ligevægtsstillingen er opnået. | 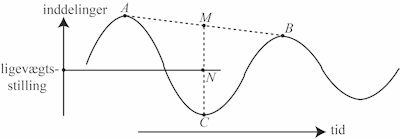 |
Principielt aftager svingningernes størrelse eksponentielt når tiden går, så matematisk set kunne man godt beregne ligevægtsstilingen ud fra denne teori. Det har Cavendish afstået fra. Han har i stedet set sig som en iagttagende fysiker og været sikker på at den beskrevne beliggenhed af ligevægtsstillingen er nøjagtig nok.
5. Cavendishs eksperimenter
Herunder viser vi til venstre Cavendishs tabel over de 17 eksperimenter, som han udførte, og til højre forklarer vi detaljerne i tabellen.
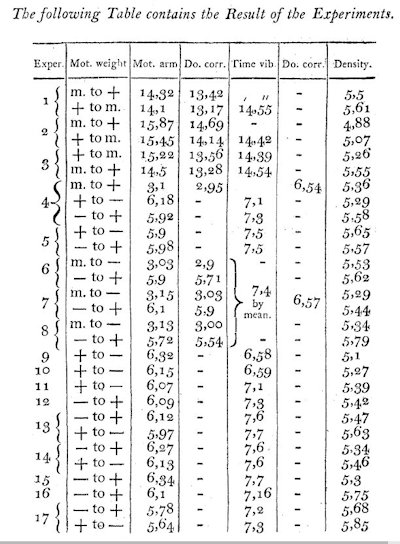 |
Efter at havde udført de tre første eksperimenter udskiftede Cavendish tråden med en anden. Som man kan se i 5. søjle bevirkede det en halvering af svingningstiderne fra ca. et kvarter til ca. 7 minutter.
Som man kan se i sidste søjle skete der
intet nævneværdigt med de beregnede vægtfylder. De korte svingningstider var mere bekvemme at måle end de lange.
Eksperiment 7 indeholder 3 linjer. Forskellen er beskrevet 2. søjle. Her betyder m.to- at svingningen sættes i gang ved at vægtene flyttes fra at være fjernt fra kuglerne til at være i den stilling, der hedder w på vores tredieøverste figur. På tilsvarende måde betyder -to+ at svingningerne sættes i gang ved at vægtene drejes fra stillingen w til stillingen W. Som man kan se i tredie søjle bevirker det - logisk nok - at antallet af inddelinger, som vægtstangen drejer sig vokser fra 3,15 til 6,1. Den tredie søjle viser den inddeling, som stangen falder til ro i efter den handling, der er beskrevet i anden søjle. Disse tal kan ikke findes ved iagttagelse, vi beskrev metoden i afsnit 4. Fjerde søjle indeholder nogle rettelser til tallene i tredie søjle. De vil ikke blive beskrevet her på siden. Femte søjle indeholder svingningstiderne i minutter og sekunder. Cavendish definerer svingningstiden som den tid der går fra en maksimal drejning af stangen til en minimal drejning. Det er halvdelen af det, som man i dag kalder en svingning. |
Som et eksempel tager vi nu den øverste af de tre linjer i eksperiment 7. Her drejer stangen sig B = 3,15 enheder på skalaen og svingningstiden N = 6´57´´ = 417 sek. Indsættes disse tal i den formel for D, som står i slutningen af afsnit 3 får vi, at D = 5,37 g/cm3. Nutidens værdi er 5,52 g/cm3. Gennemsnitet af de 29 resultater, der står i Cavendishs tabel er 5,45 g/cm3, så der er fin overensstemmelse.
6. 3 vigtige konsekvenser af Cavendishs bestemmelse af Jordens gennemsnitlige vægtfylde - I Cavendishs artikel er ingen af disse tre konsekvenser nævnt.
De dominerende bjergarter nær Jordens overflade har vægtfylde 3,5 g/cm3. Så det følger af Cavendishs måling, at der inde i Jorden må være store områder med vægtfylde væsentlig større end den gennemsnitlige. - Et faktum, som vi i dag har detaljeret kendskab til.
Når man først har fundet Jordens gennemsnitlige vægtfylde, er det let at finde dens vægt. Jordens radius r er nemlig r = 6,378 i enheden 1000 km, og hvis det indsættes i formlen for en kugles rumfang får vi, at rumfanget R af Jorden er
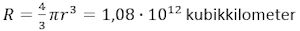
Da en kubikkilometer vand vejer 1012 kg, ville Jorden veje 1,08·1024 kg, hvis den var lavet af vand. Nu er Cavendishs værdi af vægtfylden 5,29 gram/cm3, og Cavendish kunne derfor bestemme Jordens vægt til 5,71·1024 kg. Det stemmer fint med nutidens værdi, som er 5,97·1024 kg.
Newtons tiltrækningslov siger at to legemer med vægte m1 og m2, der befinder sig i afstanden a fra hinanden, tiltrækker hianden med en kraft K af størrelsen
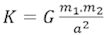
Her er G et tal hvis størrelse kun afhænger af de enheder man måler vægt, afstand og kraft med. Værdien af G var ikke kendt på Newtons tid. Faktisk var det først Cavendishs bestemmelse af Jordens vægt, der gjorde det muligt at bestemme værdien af G: Vi betragter en kugle med masse 1 kg, der ligger på jordoverfladen. Så vil tiltrækningskraften fra Jorden være 1kg*, hvor 1 kg* er defineret som den kraft, som Jorden tiltrækker et 1 kg tungt legeme på jordoverfladen med. Jorden vejer 5,97·1024 kg og afstanden er a = 6378 km. Indsættes tallene i formlen ovenfor får man, at
G = 6,8·10-18 når man bruger enhederne kg*, km og kg.
7. Afslutning
Når man skal veje noget, lægger man det naturligvis på en vægt. Så når jeg fortæller venner om, at jeg skriver om den første fysiker, der bestemte Jordens vægt, så ser de helt forkerte ud i hovedet; de forestiller sig nok noget i denne retning:


| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |