Forside Søgning Liste

Indledning

I vores biografi om den franske fysiker, madame du Chatelet (1706-1749), nævner vi et sjovt eksperiment, som hun foretog efter inspiration fra den hollandske fysiker, Willem 's Gravesande (1688-1742). Meningen med forsøget var at afklare det uldne begreb "vis viva", som optog datidens fysikere meget, og som førte til en del skænderier. Vis viva blev senere udviklet til det mere præcise begreb energi, specielt bevægelsesenergi (kinetisk energi). Biografien finder man ved at klikke på Liste her foroven og derefter på det røde link. Her i denne faglige artikel fortæller vi mere om baggrunden for forsøget og om vores egen efterligning af det.

Huygens

I 1652 havde Huygens afsluttet sine studier af sammenstødet mellem to fuldstændig elastiske kugler. Kuglerne må altså ikke være lavet af sådan noget som modellervoks. Huygens fandt to hovedresultater:

1. Det første resultat handler om det vi idag kalder bevægelsesmængde eller impuls. Når en kugle med masse m bevæger sig på en orienteret ret linje med hastigheden v defineres dens bevægelsesmængde som mv. Her skal v regnes negativ når bevægelsen går imod orienteringens retning. Huygens fandt ud af, at

   Når to fuldstændig elastiske kugler støder sammen, da er den samlede bevægelsesmængde den samme før og efter stødet.

2. Det andet resultat handler om det vi i dag kalder energi. Dette begreb kendte man ikke dengang, men man følte behovet for sådan noget. Man kaldte det lidt senere end Huygens "vis viva", "levende kraft", og for en kugle med masse m og hastighed v definerede man i nogle sammenhænge vis viva som mv². Huygens fandt ud af, at

   Når to fuldstændig elastiske kugler støder sammen, da er den samlede vis viva den samme før og efter stødet.

Gravesande og du Chatelet

I det følgende århundrede foregik der en livlig diskussion om betydningen af disse to begreber. I en lang periode omkring år 1700 var diskussionen centreret omkring to grupper, anført af henholdsvis Newton og Leibniz. Tilhængerne af Newton mente, at det centrale begreb måtte være bevægelsemængden mens Leibniz - gruppen mente, at vis viva var vigtigst.

Gravesande foretog et forsøg vedrørende vis viva ca. 1722 og sendte senere besked om det til du Chatelet, som gentog forsøget og skrev om det i sin bog Institutions de Physique fra 1740. Du Chatelet så nok tydeligere end Gravesande sammenhængen mellem Leibniz' teoretiske ideer og det eksperimentelle forsøg. Forsøget gik i hendes version ud på at finde betydningen af bevægelsesmængde og vis viva i forhold til hinanden.

Forsøget bestod i at lade en messingkugle falde ned i noget blødt ler fra forskellige højder, og så hver gang måle, hvor langt den kommer ned i leret. Gravesandes og du Chatelet's resultat var ifølge vores kilder, at fordybningen var proportional med m gange kvadratet på hastigheden v. Vi har desværre ikke kunnet finde deres måleresultater i tilgængelig litteratur, og vi har derfor bestemt os til at lave forsøget selv.

Vores forsøg

På billedet til venstre viser vi, hvordan vi tilrettelagde forsøget. Kuglen er af stål fra et kugleleje, den er 23 mm i diameter, og den vejer 55 gram. Vi foretog to mislykkede forsøg med sand, men nåede til sidst frem til, at almindigt sukker var velegnet. Vi valgte 5 forskellige højder, som var tilgængelige i den ejendom, hvor vi bor, og fra hver højde lod vi kuglen falde ned i spanden med sukker 10 gange med omrøring af sukkeret inden hvert fald. I tabellen nedenfor er der for hver højde angivet den gennemsnitlige nedtrængen og den hastighed kuglen ramte overfladen med. Vi målte kuglens nedtrængen ved at stikke en strikkepind ned i sukkeret til den ramte kuglen, og vi regnede hastigheden v ud ved at bruge Galileis formel v = √(2gh) = √(18,6·h), hvor h betyder højden.

HØJDE I METER	0,70	1,25	1,94	5,00	8,00
HASTIGHED I METER/SEKUND	3,6	4,8	6,0	9,6	12,2
NEDTRÆNGEN I CM	1,8	2,3	3,6	5,1	6,2

Som kommentar til hastighederne skal vi oplyse, at 10 m/sek er 36 km/T og at 1 m/sek derfor er 3,6 km/T. På den baggrund mener vi nok, at man kan se bort fra luftmodstanden.

Sammenhængen mellem hastighed og nedtrængen bliver klar på nedenstående graf:

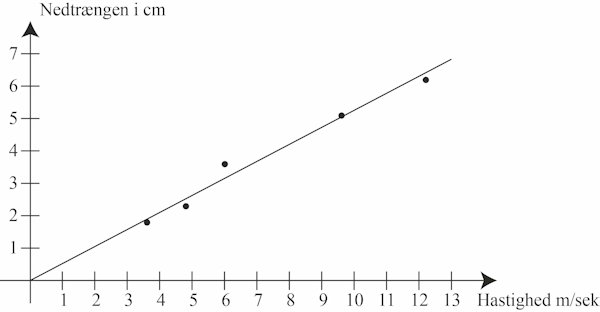
Det kom som en stor overraskelse for os, at der er en lineær sammenhæng mellem hastigheden og nedtrængningen. Vi forstår ikke, hvorfor det er sådan. Hvis forsøget havde målt bevægelsesenergien, ville der være en lineær sammenhæng mellem hastighedskvadratet og nedtrængningen. På baggrund af dette negative resultat bestemte vi os til at lave forsøget med ler i stedet for med sukker. Kilderne fortæller nemlig, at Chatelet brugte ler. Fra en keramiker fik vi fat i en meget ren klump ler beregnet til keramik, og på billederne nedenfor viser vi, hvordan vi tilrettelagde forsøget.

Vi har hængt en tommestok ned langs kanten af en dør på klem. Hvis man retter det bøjede led af tommestokken ud, når det præcis ned til overfladen af leret i skålen. Når man så bøjer tommestokken igen, kan man lade kuglen falde ned langs dørens kant så den rammer midt i skålen med ler.	Derefter stiller man skålen ned i en lidt højere skål, og måler hvor langt der er fra den hullede metalstang og ned til det øverste af kuglen. Målingen foretages med en skydelære med nonius. På billedet ser man skydelærens tynde pind, der rammer kuglens øverste punkt. På samme måde kan man måle afstanden ned til leret. På denne måde kan man måle nedsynkningen med en nøjagtighed på tæt ved 0,1 mm.

Forsøget udførtes to gange. Gennemsnittet af resultaterne vises i tabellen nedenfor:

HØJDE I CM	20	40	60	80	100	120	140	160	180	200
HASTIGHED I METER/SEKUND	1,93	2,73	3,34	3,86	4,31	4,72	5,10	5,46	5,79	6,10
NEDTRÆNGEN I MM	2,5	5,8	8,5	10,5	12,2	12,0	14,5	15,6	15,8	16,5

På billedet nedenfor viser vi grafisk, hvordan sammenhængen er:

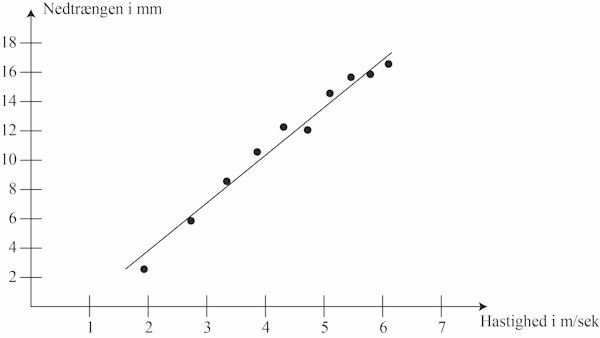
Som man kan se er der igen lineær sammenhæng mellem hastighed og nedsynkning. Så denne undersøgelse bekræfter ikke at Chatelet fandt at bevægelsesenergien er proportional med mv².

Afslutning

På wikipedia står der, at Gravesande iagttog, at hvis en kugle ramte overfladen med en hastighed, der var dobbelt så stor som en anden kugles hastighed, så ville den første kugle komme fire gange så langt ned. Det stemmer ikke med vores resultaterne af vores forsøg. Det er vores vurdering, at tankegangen bag forsøget var fornuftig, men efter udførelsen af forsøget måtte man - ærgerligt nok - erkende, at der ikke kan drages nogen konklusion af det. Forsøget målte altså ikke bevægelsesenergien. Billedet til højre har vi fundet på nettet, vi aner ikke, hvor gammelt det er, men det ligner vores forsøg. Vi tror ikke, at man kan nå et tilfredsstillende resultat, uden nærmere at undersøge hvordan nedtrængningshastigheden aftager på vejen ned.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.