Forside Søgning Liste

1. Coulombs artikel om nøjagtige målinger af snoningsmomenter

Før Coulomb havde der vist ikke været foretaget systematiske målinger af snoningsmomenter. Coulomb publicerede sine resultater i en serie lange artikler i det højt ansete tidsskrift "Memoire de l´Acedemie Royale des Sciences". For at give et indtryk af stilen starter vi med at vise en oversættelse af de første afsnit af den første artikel, der udkom i 1784:

Teoretisk og eksperimentel forskning Om snoningskræfter og elasticiteten af metaltråde. Anvendelsen af denne teori til udforskning af erfaringer i fysik. Konstruktion af forskellige snovægte med henblik på at måle størrelsen af meget små kræfter. Iagttagelser af lovene for elasticitet og brudstyrke. Af M. Coulomb AFSNIT 1 Denne artikel har to emner: det første er at bestemme den elastiske snoningskraft for tråde af jern og messing, udtrykt ved trådens længde og tykkelse og graden af snoning. Jeg havde derfor behov for, i en artikel om magnetnåle trykt i neuvieme volume des Savant etrangers at bestemme snoningskræfterne for hår og silke. Men jeg har først og fremmest beskæftiget mig med metaltråde, fordi det materiale jeg skal vælge, skal tåle stor stramhed, og fordi jeg har fundet at silketråde har uden sammenligning mere fleksibilitet end metaltråde. Det andet emne for denne artikel er at vurdere det uperfekte ved den elastiske reaktion af metaltråde, og undersøge hvad de konsekvenser man kan drage i forhold til relationen mellem styrke og elasticitet af legemer. AFSNIT 2 Metoden til eksperimentelt at bestemme snoningskræfter består i af ophænge en cylindrisk vægt i en metaltråd, således at dens akse er lodret, dvs i retning af ophængningstråden, se Fig 1. Sålænge ophængningstråden ikke er snoet sker der intet med cylinderen. Men hvis man begynder at dreje vægten omkring sin akse snor tråden sig og den prøver at genetablere den naturlige situation. Hvis man slipper vægten, så svinger den frem og tilbage i tidens løb, den følger mere eller mindre den elastiske snoningskraft. Hvis man under dette forsøg observerer varigheden af et bestemt antal svingninger, er det ved hjælp af formlen for svingende bevægelser let at bestemme den snoningskraft, som forårsager disse svingende bevægelser. Og hvis man varierer vægten af cylinderen og længden og tykkelsen af ophængningstråden kan man finde loven for snoningskraft udtryket ved længden, tykkelsen og materialet af tråden. AFSNIT 3 Hvis metaltråden er fuldstændig elastisk, og hvis luftmodstanden ikke påvirkede svingningernes størrelse ville vægten, når den én gang er sat i bevægelse, svinge indtil man standser den. Formindskelsen i udsvingenes størrelse kan næppe skyldes luftmodstanden eller den uperfekte snoningskraft. Derfor vil det være sådan, at når man observerer en varig aftagen af svingningernes amplitude, og ser bort fra den del af formindskelsen, der skyldes luftmodstanden, så kan man ved hjælp af formlerne for en svingende bevægelse, anvendt på denne situation, finde ud af hvilken lov snoningskræfterne følger. AFSNIT 4 Denne artikel er delt i to dele: I den første bestemmes loven for torsionskræfter, idet man antager, at de er proportionale med drejningsvinklen, en antagelse, der stemmer overens med erfaringen, såfremt man ikke anvender en alt for stor snoningsvinkel. I den anden del undersøger vi, baseret på eksperimenter, hvilken lov der gælder for for svingninger med store amplituder. Vi vil bruge disse resultater til at at undersøge sammenhængskraften og elasticiteten når der er tale om tunge legemer. AFSNIT 5 F Ø R S T E S E K T I O N. Formler for svingende bevægelse under forudsætning af at snoningskraften er proportional med snoningsvinklen eller påvirket af en meget lille grænse.

Hermed slutter jeg med oversættelsen af Coulombs artikel.

På Coulombs tid var reglen om bevarelse af energi ikke erkendt. Men i det specielle tilfælde, hvor der alene er tale om bevægelsesenergi, vidste man godt at størrelsen ½mv² bevares. Her viser jeg ved anvendelsen af denne regel, sådan som den er beskrevet under 1781 inertimoment, hvordan man kan komme videre med beskrivelsen af, hvordan Coulomb kunne måle meget små snonongsmomenter.

Vi starter med at sætte cylinderen i rotation omkring den lodrette akse. Og så lader man den frit udføre svingninger. Så skal trådens egenskaber være valgt sådan, at man bekvemt kan aflæse den tid T, som en fuld svingning tager, altså den tid der går fra tråden er snoet mest, til den næste gang er snoet mest i samme retning. Det viser sig, at inden for rimelighedens grænser er T uafhængig af svingningernes størrelse. T er altså et kendt tal.

Et cylinder er ophængt i en tråd således at cylinderens akse er lodret og befinder sig i forlængelse af ophængningstråden. Så drejer man cylinderen om sin akse, så aksen stadig er lodret, og vi vil nu bestemme en formel for svingningstiden, under antagelse af at snoningsmomentet er proportional med drejningsvinklen.

Den variable drejningsvinkel v = v(t) regnes med fortegn, se f.eks. den øverste figur på siden om inertimoment. Vinkelhastigheden ω er så den afledede ω = v´(t). Det eneste drejningsmoment, der virker på cylinderen er så drejningsmomentet fra den snoede tråd, og erfaringen viser, at dette drejningsmoment H er proportionalt med v, og rettet tilbage mod ligevægtsstillingen, H = - H₁v. Her er H₁ det drejningsmoment, som tråden påvirker cylinderen med, når tråden er snoet 1 radian. Coulombs tråde var så lette at sno, at det var meget svært at måle dette drejningsmoment. Ikke desto mindre var det det, som Coulomb gjorde.

Inertimomentet I for en cylinder er som nævnt kendt. Ifølge slutresultatet i 1781 inertimoment gælder der

I vores artikel om drejningsmoment, se link for oven, har vi nævnt, at en funktion ω = ω(t), der opfylder ovenstående differentialligning, kan skrives på formen

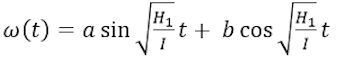
Denne funktion er periodisk med perioden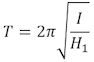

. Her er I og T kendte tal

Periodens længde T kan bestemmes med god nøjagtighed ved at man sætter svingningen i gang, noterer tiden for et passende antal svingninger og så dividerer. Så kan man af formlen for T beregne drejningsmomentet H₁. Dette drejningsmoment er det moment, der påvirker cylinderen, når tråden er snoet 1 radian. Dette svage moment ville det være meget vanskeligt at bestemme på andre måder end ved at løse ovenstående differentialligning.

Det er en fantastisk opdagelse, at man ved at måle den let iagttagelige svingningstid kan beregne snoningsmomentet H₁. Man kan matematisk bevise, at formlen for svingningstiden også gælder, når der er tale om en dæmpet svingning, hvor dæmpningen er proportional med svingningshastigheden. Dette er vigtigt i teorien for den snovægt, som vi beskriver nedenfor.

De udregninger, som Coulomb udførte i stedet for ovenstående, har jeg meget svært ved at forstå. Du kan se mine vanskeligheder her.

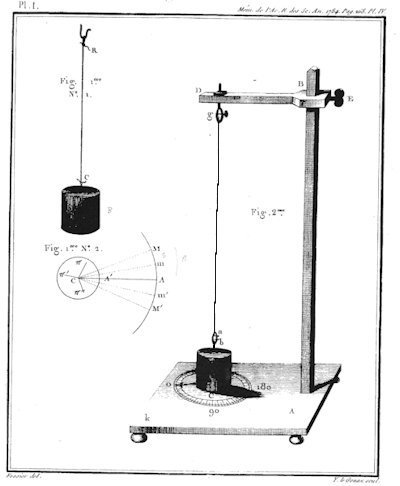
Vi går nu over til at beskrive Coulombs forsøg på at bestemme snoningsmomenterne. På en lille plade AK med fire runde ben er der oprejst en lodret galge ABD, som er ca 1,2 meter høj. Den vandrette stang DB sættes fast med skruen E. Cylinderen P hænger i i tråd, der foroven er spændt fast med skruen ved g. Det er kun tråden herfra og ned til skruen ved a, der kan snos. Nede på pladen Ak er der fastgjort en tynd cirkulær plade med gradinddeling. Pladens centrum befinder sig i forlængelse af tråden. Jeg gætter på, at cylinderens underside befinder sig et par mm over pladen Ak. På undersiden af cylinderen er der fastgjort en viser, der peger på o. Men den kan man aflæse drejningsvinkler. Coulomb nævner, at hans jerntråde er fabrikeret til brug i et cembalo, en form for klaver. Han får tråden på en spole, og han nævner i forsøg 5, at det er en fejlkilde, at tråden med svag belastning er tilbøjelig til at krumme sig.

Nedenfor går vi over til at beskrive 13 af Coulombs forsøg med snoning af metaltråde. Han brugte tråde af messing og jern. I vores beskrivelse vælger vi nutidens enheder, så vi starter her med at angive sammenhængen mellem Coulombs enheder og nutidens:

1 grain = 6,5 gram; 1 once = 30 gram; 1 livre = 500 gram; 1 ligne = 0,25 cm; 1 pied = 30 cm.

FORSØG NR.	TRÅD				CYLINDER			DREJNING		KOMMENTARER
	Længde i cm	Metal	Brudstyrke i kg.	Vægt i gram af 180 cm	Vægt i gram	Radius i cm	Højde i cm	Vinkel	Sek. for 10 svingninger
1	2,2	Jern	1,86	32,5	250	2,5	1,6	<180°	120
2	2,2	Jern	1,86	32,5	250	2,5	1,6	3×360°		Ikke ligetidigt
3	2,2	Jern	5	90	250	2,5	1,6	180°	42
4	2,2	Jern	5	90	1000	2,5	6,4		85
5	2,2	Jern	16,5	364	250	2,5	1,6	1080°		Ikke ligetidigt
6	22,5	Jern	16,5	364	1000	2,5	6,4	<45°	23
7	22,5	Messing	1,1	32,5	250	2,5	1,6	<360°	220
8	22,5	Messing	1,1	32,5	1000	2,5	6,4	9	442
9	22,5	Messing	7	120	250	2,5	1,6	<360°	57
10	22.5	Messing	7	120	1000	2,5	6,4	<360°	110
11	22,5	Messing	11	430	250	2,5	1,6			Ikke ligetidigt
12	22,5	Messing	11	430	1000	2,5	6,4	<50°	32
13	90	Messing	7	120	1000	2,5	6,4	<1080°	222

Vi går nu over til at vurdere de opnåede resultater:

Det første resultat af forsøgene er, at når drejningsvinklen ikke er alt for stor, så er svingningerne ligetidige. Det betyder, at den tid T der går, fra cylinderen er i en yderstilling, til den igen er i en yderstilling til samme side, ikke ændrer sig under det enkelte forsøg. Som tidligere nævnt gælder det, at

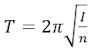
hvor I er cylinderens inertimoment, og hvor n er snoningsmomentet, når cylinderen er drejet 1 radian væk fra ligevægtsstillingen. n er Coulombs betegnelsen for det tal, som vi tidligere har kaldt H₁. Forudsætningen for ovenstående formel er som nævnt, at snoningsmomentet er proportionalt med drejningsmomentet, og det stemmer med at vi iagttager, at svingningerne er ligetidige.

I vores omtale af inertimoment - der er link for oven - har vi fundet, at cylinderens inertimoment er I = ½Ma², hvor M er cylinderens vægt, og a er dens radius. Svingningstiden bliver derfor

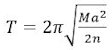
Heraf følger, at hvis man laver to forsøg, der kun afviger fra hinanden med størrelsen af M, så vil T være proportional med √M. Det betyder f.eks., at hvis man gør M 4 gange større, så vil svingningstiden blive fordoblet. Dette kan man iagttage i forsøgene 3 og 4, og man kan også iagttage det i forsøgene 7 og 8.

På figuren til højre viser vi tråden fra den nederste ende, hvor cylinderen skal hænge, og op til den trådens øverste ende, som vi tænker os fastgjort på en plade, som ikke kan bevæges. Diameteren af tråden er tegnet voldsomt overdrevet. Vi betragter en situation hvor tråden forneden er påvirket af et snoningsmoment af størrelsen m = K·a, og hvor svingningerne er faldet til ro, så der er ligevægt. Så må tråden foroven af pladen være påvirket at et modsat rettet moment af støttelsen -m, ellers vi der starte en snoning. DDu kan finde en begrundelse på vores side om drejningsmoment, der er link for oven. På figuren har vi i en tilfældig højde placeret et snit S i tværs igennem tråden. Så vil den del af tråden, der ligger over S påvirke den del af tråden, der ligger under S med et moment af størrelsen, -m, ellers vil der ikke være ligevægt. Omvendt må den del af tråden, der ligger under S påvirke delen over S med et moment af størrelsen m. De nævnte påstande er rigtige også i den situation, hvor tråden ikke er lige tyk hele vejen.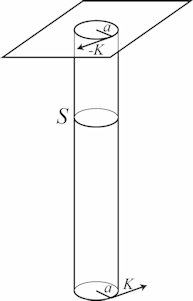

Nu forudsætter vi så, at tråden er ensartet i hele sin længde, dvs. at den har samme tykkelse og den er lavet af samme materiale hele vejen igennem. Så vil en snoning fordele sig jævnt over hele snorens længde.

Vi betragter nu den specielle situation, hvor der er ligevægt og hvor tråden tråden forneden er snoet 1 radian. Tråden er derfor forneden påvirket af et drejningsmoment af den størrelse n, som vi har nævnt ovenfor. Vi tænker os nu, at snittet S på figuren ovenfor er placeret ⅓ af trådlængden under pladen for oven. Så må trådstykket fra pladen til S være snoet ⅓ radian. Hvis vi nu fjerner trådstykket nedefra til S, skal der derfor et drejningsmoment af størrelsen 3n til at sno den korte snor 1 radian. Hvis vi erstatter 3 med x får vi et bevis for, at n er omvendt proportional med snorlængden.

Vi har hermed beskrevet indholdet af den første trediedel af Coulombs artikel fra 1784. Den del af artiklen indeholder de centrale resultater, og de er tilstrækkelige til at man kan forstå den efterfølgende artikel fra 1785.

Coulomb blev medlem af Videnskabernes Selskab i Paris i 1782 og i 1785 publicerede han sit arbejde om elektricitet i en artikel i selskabets annaler. Billedet nedenfor er hentet fra denne artikel. Det fremgår af teksten øverst på billedet. Billedet viser den snovægt (på nudansk torsionsvægt), som Coulomb konstruerede for at kunne måle elektrisk tiltrækning og frastødning mellem små elektrisk opladede hyldemarvskugler. Der er tale om kræfter, der er langt mindre end dem, man tidligere kunne måle. Det centrale element i snovægten er et legeme ophængt i en tynd metaltråd, men Coulomb opdagede snart, at omhyggelige målinger krævede at tråden og det svingende legeme blev indesluttet i en beholder. Ellers ville bevægelserne i luften forstyrre målingerne.

2. Coulombs artikel om snovægten og nøjagtige målinger af elektrisk tiltrækning og frastødning Store dele af det følgende er oversættelser af Coulombs artikel. Når der står "jeg" betyder det altså Coulomb, og ikke denne sides forfatter. 1.Indledning I den første artikel har jeg ud fra forsøg bestemt lovene for snoningskraften i en metaltråd, og jeg har fundet, at denne kraft, som afhænger af snoningsvinklen, er proportional med 4. potens af ophængningstrådens diameter og omvendt proportional med trådens længde. Det hele skal man dog multiplicere med en konstant koefficient, som afhænger af metallets natur, og som er nem at bestemme ved forsøg. Jeg har også forklaret i den samme artikel, at ved hjælp af denne snoningskraft er det muligt med stor præcision at måle meget små kræfter, som f.eks. 1:10.000 grain (= 0,00065 gram, altså ½ milligram). Grain er en gammel engelsk vægtenhed. 1 grain er ca. 6,5 gram. Jeg præsenterer her for akademimedlemmerne en elektrisk vægt som er konstrueret efter de samme principper. Den måler med størst mulig nøjagtighed både elektrisk ladning og elektriske kræfter. 2.Konstruktionen af Snovægten Uagtet erfaringen forekommer det mig, at hvis man på en hensigtsmæssig måde skal udføre nye elektriske forsøg, er det nødvendigt at rette nogle mangler ved det første apparat jeg har lavet inden for dette område. Figur 1 viser perspektivisk denne snovægt, så se detaljerne der. På en glascylinder ABCD, som er 12 tommer i diameter og som er 12 tommer høj placerer man et glaslåg der er 13 tommer i diameter. Det dækker hele glaskarret. I låget er der to huller på 20 lignes. Det ene er i midten af låget, ved f. Op fra dette står der et rør af glas, der er 24 tommer højt. Dette rør er limet fast over hullet ved f, med en lim som man plejer at bruge i elektriske apparater. I den øverste ende af røret er der ved h placeret et snoningsmikrometer, som man kan se i detaljer på figur 2. Den øverste del, no1, bærer knappen b, en viser io og bærepinden q. Denne del går ned i hullet G på no2. Denne del, no2, er formet som en cirkel ab, og dens rand er inddelt i 360°. Under den er der en cylinder Φ, som går ned i hullet H i no3 som er tilpasset til det indre af det lodrette rør fh på Fig.1. Holderen q på Fig.2, no1 er formet som en blyantsholder. Det er på spidsen af denne at der er fastgjort en meget tynd tråd af sølv. Den nederste ende af denne tråd, se fig3, er fastgjort i spidsen af en cylinder po, der er lavet af kobber eller jern og som er formet som spidsen af q ved den øverste ende af tråden, hvis diameter ikke overstiger en ligne (dvs 2,25 mm) og hvis ende P er formet som en lukkering Φ. Denne lille cylinder er sat fast oven på vægtstangen ved C, så vægtstangen ag ikke glider. Det er nødvendigt, at denne lodrette stangs vægt er tilpas stor til at holde sølvsnoren stram, uden at den går i stykker. Som man ser på fig 1 er ag er ophængt vandret i midten i midten af den store skål, som omslutter den. Stangen ag er et strå, der er smurt ind i spansk voks og er omviklet med en silketråd, der ligeledes er smurt ind i spansk voks, og som forløber fra q til a. Længden er 18 lignes (dvs 40 mm). : I enden af af denne vægtstang er der en lille kugle af hyldemarv; den er 2 til 3 lignes i diameter I den anden ende g er der en lille lodret skive af papir, der er smurt ind i terpentin som tjener som kontravægt til kuglen a, og som dæmper svingningerne. Vi tilføjer, at der i låget AC også er et andet hul ved m. Det er genem dette hul man sænker den lille cylinder mΦt ned i skålen. Den ses kun vanskeligt på figuren. Dens nederste del Φt er også af shellak. Ved t er der også en kugle af hyldemarv, magen til den anden. I højde med vægtstangen er der rundt om glasskålen en inddeling på 3630 grader. For simpelheds skyld lavede jeg en papirstrimmel, delt i 360 grader, som jeg limede rundt om glasskålen. 2. Coulombs brug af snovægten. Før jeg begyndte af anvende dette instrument, måtte jeg placere låget sådan , at hullet m var ud for nulpunktet i den ydre gradinddling. Jeg placerede også viseren oi på mikrometret for oven, så den pegede på nulpunktet af mikrometrets inddeling. Dernæst drejede jeg mikrometret på toppen af røret sådan at hyldemarvskuglen på vægtstangen ag også også var ud for nulpunktet på papirstrimlen, der var limet rundt om glasskålen. Jeg indførte dernæst, gennem hullet m, den anden hyldemarvskugle t, der sidder i enden af stangen mΦt, på en sådan måde at de to hyldemarvskugler rørte hinanden ud for nulpunktet på papirstrimlen, se Fig 1 nedenfor. Vægtstangen er faktisk i stand til at udføre alle de operationer, der er nødvendige, når man ville bestemme den kraft som elektrisk opladede kugler frastøder hinanden med. Den fundamentale elektricitetslov Den frastødende kraft mellem to små kugler, der bærer samme slags elektricitet, er omvendt proportional med kvadratet på afstanden mellem de to kugler. Eksperimentet. Man sørger for, at viseren for oven står på 0 når vægtstangen er i ro og kuglen a er ud for 0° mærket på papirstrimlen. Så oplader man en lille elektrisk leder, som er en nål med et stort hoved, som er isolert ved at der i spidsen er fastgjort en stang af shellak. Man fører så denne elektrificerede nål ned i hullet m i låget, se figuren ovenfor, og lader hovedet røre ved kuglen t, som også rører ved kuglen a, se Fig.1 nedenfor, hvor vægtstangen ag er set fra oven.          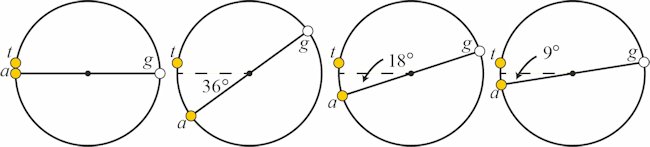Fig.1        Fig.2         Fig.3         Fig.4 Nu er de to kugler blevet opladet med elektricitet af samme slags, og de frastøder hinanden til en afstand som man kan måle ved at iagttage beliggenheden af kuglen a på påpapirstrimlens inddeling. Når man så drejet viseren o med uret snor man ophængningstråden, og man skaber den kraft, proportional med drejningsvinklen, som fører kuglen a hen til kuglen t. Ved at sammenligne torsionskræfterne med de tilsvarende afstande kan man bestemme den lov, der bestemmer frastødningen. Jeg nævner her, hvilke forsøg det er nødvendigt at gentage og som fører til frastødningsloven. Første forsøg starter som nævnt med, at de to kugler a og t placeres ud for 0°-mærket på papirstrimlen, Fig.1. Når man så oplader de to kugler som beskrevet ovenfor får de samme ladning, frastøder hinanden og vægtstangen ag drejer sig og falder til ro med en drejningsvinkel på 36°, Fig.2. Andet forsøg. Hvis man så drejer viseren o 126°, så nærmer de to kugler sig hinanden indtil der er 18° mellem dem. Tredie forsøg. Hvis man drejer viseren o 567°, så nærmer de to kugler sig hinanden til en afstand på 8½°. Forklaring og resultat af disse forsøg. Så længe kuglerne endnu ikke er elektrisk opladede rører de hinanden, og centret af kuglen a, der sidder i enden af vægtstangen er ikke længere væk fra det punkt, hvor tråden ikke er snoet, end halvdelen af de to kuglers diametre. Det er nødvendigt at være opmærksom på, at sølvtråden lp, som skaber snoningskraften er 28 tommer lang, og tråden er så tynd, at vægten af 30 cm ikke er mere end 0,4 gram. Når man skal udregne den kraft, som virker på a og som er nødvendig for at sno den tråd skal man benytte at a er 4 tommer fra tråden, så har jeg brugt de formler, som jeg har forklaret i volume de l´Acedemie pour 1784. For at sno denne tråd 360° er det nødvendigt i a at anvende en kraft på 1/340 grains (0,02 gram). Som jeg har vist i den nævnte artikel er snoningskraften proportional med drejningsvinklen, så jo mindre frastødningskraft der er mellem de to kugler, jo mindre fjerner de sig fra hinanden. Vi fandt i vores første forsøg, hvor viseren peger på o, at kuglerne fjerner sig 36° fra hinanden, og det skaber altså en snoningskraft på 1/3400 grains (2 mg). I det andet forsøg var afstanden mellem kuglerne 18°, altså halvt så stor som i første forsøg. Men da man har drejet mikrometret 126° er resultatet, at ved en drejning på 18° er den samlede drejning 144°; det er det er 4 gange så meget som i første forsøg. I det tredie forsøg har man drejet viseren 567°, og de to kugler er kun 9° fra hinanden. Den samlede snoning er 567 + 9 = 576°, som er 4 gange så stor som i andet forsøg, og kuglernes afstand er halvt så stor som den var i andet forsøg. Resultatet af disse tre forsøg er altså, at frastødningskraften mellem to ens opladede kugler er omvendt proportional med kvadratet på afstandene. En første bemærkning. Ved gentagne forsøg af denne art finder man, at egenskaberne af en sølvtråd af så høj kvalitet som vi har kunnet skaffe, og som kun gav en snoningskraft på omtrent 24 tusindedel grain, ved en snoning på 5 ° alligevel gav en usikkerhed på 2 eller 3 grader i aflæsningen. Også, for at få et forsøg man kan sammenligne med i det følgende, er det nødvendigt efter at kuglerne er opladede at sno tråden 30° eller 40°. Det giver en tydelig torsionskraft og man må acceptere en usikkerhed på 2° til 3° i udgangspositionen af vægtstangen, hvor snoningskraften er 0. Det giver ikke nogen betydelig usikkerhed i resultaterne. Man må også være opmærksom på at tråden, som jeg benyttede mig af ved disse eksperimenter er så tynd, at den kan gå i stykker på grund af små rystelser. Jeg har senere fundet ud af, at det kan være mere bekvemt at bruge en tråd med den dobbelte diameter, selv om torsionskraften bliver måske 14 - 15 gange større end med den tynde tråd. Det kan være nødvendigt, før man bruger denne sølvtråd at holde den snoet i to eller tre dage med en vægt nær ved halvdelen af den, der kan knække tråden. Det er endvidere nødvendigt at være opmærksom på, at når man bruger den sidst nævnte sølvtråd, er det aldrig nødvendigt at sno den omkring 300°, for hvis man passerer denne grad af snoning kan det ske, at den ikke reagerer som beskrevet i den tidligere artikel fra 1784, men have halvdelen af den kraft, der svarer til torsionsvinklen. Anden bemærkning. Elektriciteten på de to kugler formindskes en smule i løbet af et eksperiment. Jeg har erfaret, at på den tid det tog at udføre de nævnte eksperimenter, hvor kuglerne var 30° fra hinanden og snoningsvinklen var 50° nærmede kuglerne sig 1 grad på 3 minutter. De tre forsøg, som jeg har beskrevet kunne udføres på 2 minutter. Derfor kan man i denne sammenhæng se bort fra denne fejlkilde. Hvis man ønsker en større nøjagtighed, eller hvis luften er fugtig, så elektriciteten udlignes hurtigere, så kan man iagttage, hvor stor formindskelse der er i elektricitetsmængde hvert minut, og benytte det til at korrigere forsøgsresultaterne på det tidspunkt. Tredie bemærkning. Afstanden mellem de to kugler, som er frastødt fra hinanden af elektriske kræfter er ikke præcist målt af den vinkel de danner, men af korden i den bue, der forbinder deres centre. På samme måde, hvis man bruger viseren for oven, skal afstanden ikke måles ved halvdelen af det, som nålen peger på, men som cosinus til halvdelen af den vinkel de to kugler danner. Man kan benytte den beregningsmåde, som vi har anvendt, hvis afstanden mellem de to kugler ikke overstiger 25 til 30 grader. I andre tilfælde er det nødvendigt at lave en præcis beregning. Fjerde bemærkning. Man kan i et godt tillukket værelse med den først nævnte sølvtråd bestemme den position af vægtstangen, der giver en snoning på 0° med en nøjagtighed på 2 til 3 grader. Når dette er gjort kan man måle snoningskraften, der er proportional med snoningsvinklen med en nøjagtighed på 40 tusindedel grains. For at udføre dene skal man bruge Fig.5 på den store figur. Der er en prop af shellak, en tynd kobberstang cd, der ender i en krog foroven, og som forneden har en hyldemarvskugle d. Denne stang stikker man ned i hullet m på Fig.1, og det er sådan, at kuglen d kommer ned i højde med målestrimlen ud for denne strimmels nulpunkt. Når man så nærmer et elektrisk legeme til krogen c, så vil kuglen a fjerne sig fra kuglen d og afstanden mellem de to kugler bestemmer frastødningskraften, der jo er omvendt proportional med kvadratet på afstanden. 3. En afsluttende kommentar fra forfatterne af hjemmesiden Hermed afslutter vi omtalen af de målinger af elektricitet, som Coulomb udførte. Faktisk kunne Coulomb på baggrund af sine målinger have defineret en enhed for elektricitetsmængde. Det gjorde han imidlertid ikke. Til gengæld kaldes den enhed, som i dag bruges for elektricitetsmængde for 1 coulomb. I en følgende artikel undersøgte Coulomb også magnetisk frastødning. Coulombs påvisning af at elektrisk frastødning er omvendt proportionel med kvadratet på afstanden bygger ikke på, at han kan måle størrelsen af de svage kræfter. Ikke desto mindre blev Coulombs metode til måling af svage kræfter senere brugt ved Henry Cavendish´s måling af Jordens vægt i 1798, der er link for oven.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.