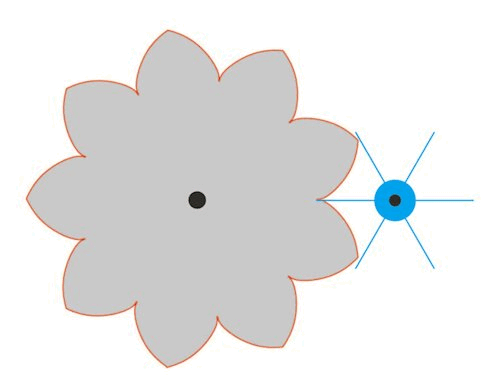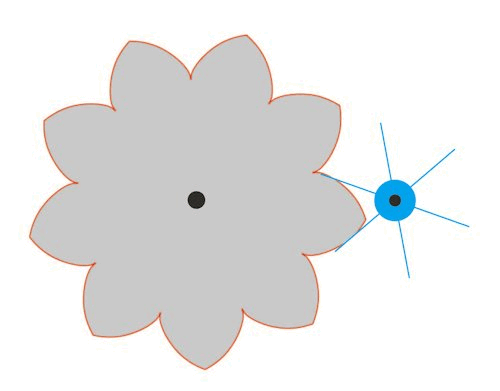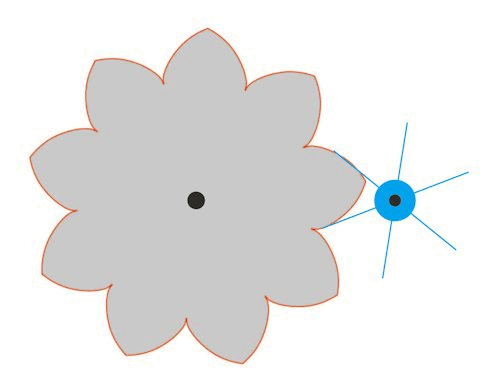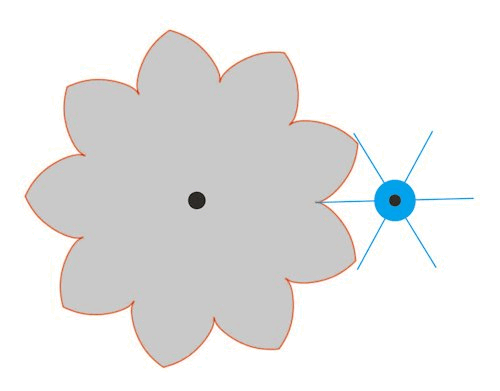
Nedenfor bringer vi en oversættelse af Eulers eksempel 1 fra den supplerende artikel om tandhjul.Det er side 215-216 i det originale manuskript. Figuren forestiller to tandhjul med centre i B og A. Kurven NOF er den ene side af en tand på tandhjulet med centrum B, og kurven MOE er den ene side af en tand på tandhjulet med centrum A. Figuren er Eulers egen, Og du vil hurtigt opdage at Euler her ikke er særlig pædagogisk. Her kommer Eulers tekst:
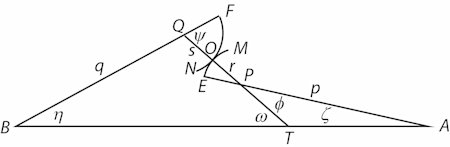
Vi tænker os at kurven EM falder sammen med radius AE og at røringspunktet O falder sammen med punktet P. TP vil altså være normal til AE. Derfor er φ = 90° og r = 0.
Derfor vil sinω = p/a, og ζ = ω - 90°.
Da dφ = 0 vil krumningsradius for tanden på hjulet med centrum B være
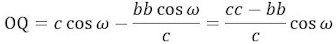
Først er det altså sådan, at p=AP ikke kan antages at være større end AT = a, men hvis p = a bliver ω = 90°, ζ = 0 og OQ = 0, således at tanden FON må have uendelig stor krumning, hvilket ikke kan lade sig gøre. Derfor er det nødvendigt, at AP = p er mindre end a. Heraf følger, at hvis p = f så vil sinω = f/a og
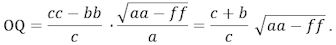
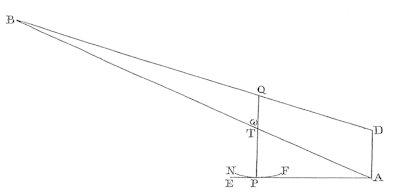
14. Konstruktionen vil altså forløbe således: Når det første hjuls radius er AE = a, så lad os i punktet P, som er nærmere centrum end a oprette den vinkelrette ud fra A og dernæst afsætte AT = AE = a og lad os forlænge AT til B så BT = b. B er altså centrum i det andet hjul. Længden af AP betegnes f, og da AT = a vil
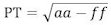
og også, at
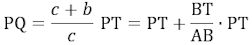
Derfor, når den rette linje AD = PT tegnes vinkelret på EA, så vil den rette linje BD bestemme punktet Q ud fra hvilket radius QP beskriver cirkelbuen FPN, som er tandformen, der hører til det andet hjul. Denne bue bør være meget lille, og ikke større end at når de følgende tænder griber ind i hinanden, så skal al handling stoppe her. Formålet er, at hvis F og N er enderne af den anden tand, så passer det sig ikke at fortsætte ud over dette, men snarere bør tanden formindskes, når de øvrige tænder nærmer sig hinanden.