Forside Søgning Liste

Om Eulers afsluttende påstand i hans supplerende artikel om tandhjul

Den schweitziske matematiker Leonhard Euler offentliggjorde i 1753 og 1767 to omfangsrige artikler om formen af tænderne på tandhjul. Euler skrev ikke artiklerne på grund af en teknisk behov, han skrev dem, fordi det matematisk set er interessant at undersøge, hvordan det er hensigtsmæssigt at forme tænderne på tandhjul.

Vi kalder her to tandhjul i indgreb for jævne, når det er sådan, at når det ene tandhjul bevæger sig med konstant vinkelhastighed, så vil det andet også dreje sig med konstant vinkelhastighed. Eulers hovedresultat i artiklen fra 1767 er en nødvendig og tilstrækkelig betingelse for, at to tandhjul er jævne. Herunder viser vi Eulers egen figur, der illustrerer betingelsen:

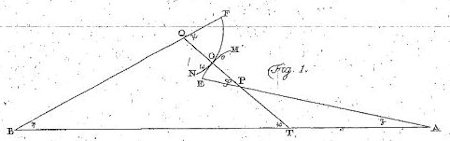
A og B er centre for to tandhjul i indgreb. T er det punkt på linjen AB for hvilket forholdet AT/BT er lig med forholdet mellem antallet af tænder på hjulet med centrum A og antallet af tænder på hjulet med centrum B. Buen EOM er formen på den ene side af en tand på hjulet med centrum A, og buen FON er formen på den anden side af en tand på hjulet med centrum B. Eulers hovedsætning siger så, at tandhjulene er jævne når og kun når den fælles normal til de to tænder i røringspunktet O hele tiden går gennem punktet T. -Der er link til beviset for oven.

I artiklen skriver Euler med visse upræcise forbehold, at hvis man skal konstruere to jævne tandhjul, og hvis en anden person, måske en fjende, bestemmer formen på tænderne i det ene tandhjul, så kan Euler beregne formen på tænderne i det andet tandhjul, således at tandhjulene er jævne. Euler beskriver fremgangsmåden i sit Eksempel 1, som vi nu går over til at gennemgå.

Euler betragter her det tilfælde, hvor fjenden har valgt en højst uventet tandform, nemlig et linjestykke, der drejer sig om den ene ende. Set fra en teknikers synspunkt er det et håbløst valg, men Euler har valgt det, fordi det er en matematisk udfordring at konstruere et par af jævne tandhjul, hvor det ene tandhjuls tænder er rette linjestykker.

Det er Euler, der skal vælge antallet af tænder på de to tandhjul. Han har imidlertid overladt valget til læseren, og jeg vælger, at der skal være 6 tænder på det retlinede tandhjul med centrum A og 9 tænder på det tandhjul, der har centrum B. BT er derfor halvanden gange så stor som AT. Endvidere vil det være sådan, at hvis tandhjulet med centrum B drejer sig 1° på 0,1 sek., så vil så vil tandhjulet med centrum A dreje sig -1,5° i 0,1 sek.

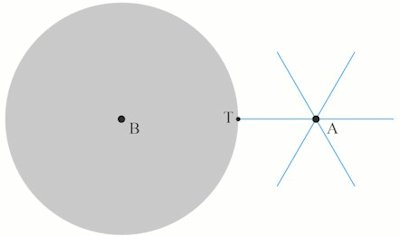
Situationen er nu den, der er vist på figuren ovenfor, og det er opgaven, at konstruere formen på de tænder, der skal sættes på den grå skive. Og her er Euler hjælpsom nok:

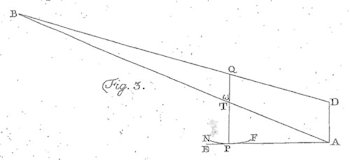
På figuren ovenfor er AE en retlinet tand i vilkårlig beliggenhed. Så tegner Euler et linjestykke TP, der fra T går ned til tanden og står vinkelret på denne. Så må P ifølge hovedsætningen være det punkt, som den retlinede tand har fælles med en tand på det andet tandhjul. Når man har konstrueret dette punkt, skal det gøres fast til den roterende grå skive på figuren ovenfor. Jeg viser nedenfor tre par eksempler på, hvordan det foregår i vores tilfælde. Formålet er at konstruere mange punkter på en bestemt tand på det grå tandhjul

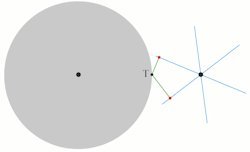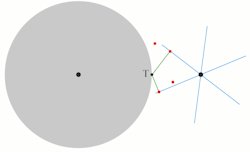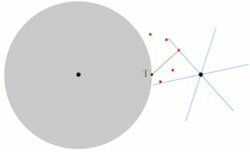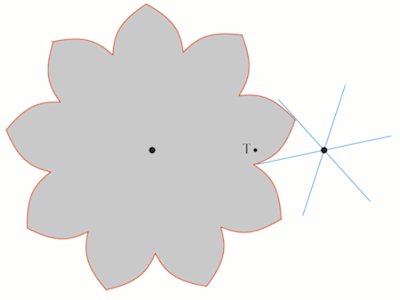
Normalt vil det blå tandhjul røre ved den søgte tand i to punkter. De grønne linjestykker fra T står vinkelret på en blå tand	Her har vi drejet de to fundne røde punkter og den grå skive 10° i forhold til den foregående stilling, og vi får så to nye punkter af den søgte tand.	Her har vi drejet de fire fundne røde punkter og den grå skive 5° i forhold til den foregående stilling, og vi får så et nyt punkt af den søgte tand.

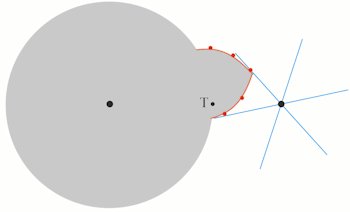Man kan uden besvær bestemme mange punkter på den søgte tands rand. Resultatet er, at tanden kommer til at se ud som på figuren ovenfor. Randen er ikke en del af en cirkel. Den krummer mest nærmest ved hjulets centrum. Den rand, jeg har tegnet ind, er en del af den epicykloide, som Rømer ville have oplyst Euler om, hvis der havde været kommunikation mellem dem.	Når man først har fundet formen på en tand, bliver tandhjulet færdigt, når man kopierer og drejer den fundne tand 8 gange. Så nu er tandhjulet færdigt. De to tandhjul er jævne, for man har jo sørget for, at fællesnormalen i et røringspunkt hele tiden går gennem T.

Nu da vi kender formen på begge tandhjul, kan jeg lave en animation af tanhjulenes bevægelse:

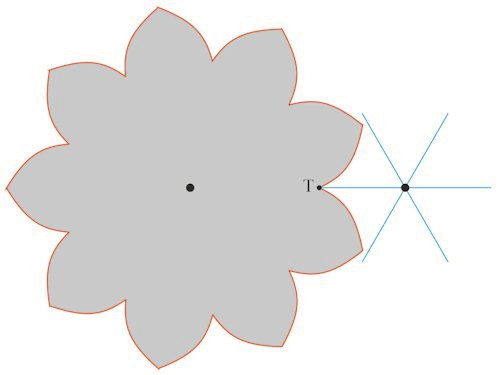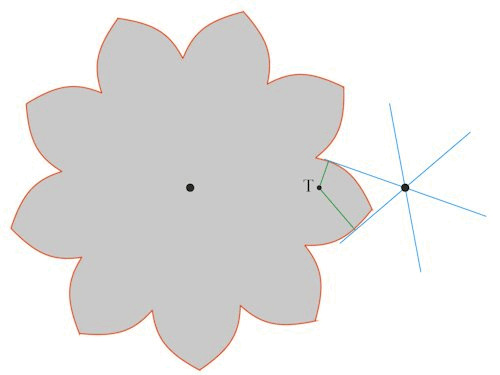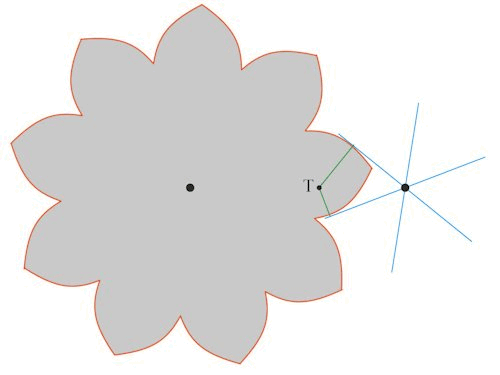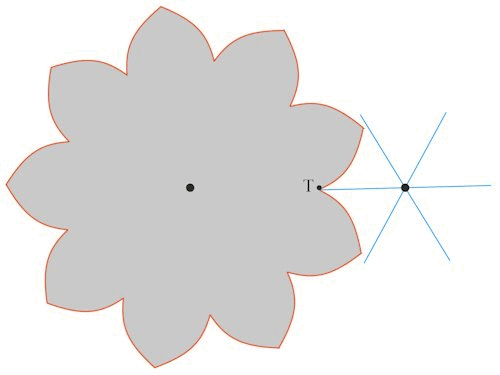
På animationen har jeg vist de grønne normaler i røringspunkterne, som ovenfor blev benyttet til bestemmelse af det grå hjuls tandform.

Det er et interessant faktum, at Euler ikke beskæftiger sig yderligere med den kurve, der begrænser tænderne. Spørgsmålet er, om det er en kendt kurve, eller om denne kurve ikke har været beskrevet før.

Euler kendte ikke Ole Rømers konstruktion af jævne tandhjul, men hvis Rømer havde fået spørgsmålet, kunne han straks have svaret på det: På billedet til højre er der tre cirkler. Det lille sorte punkt ved T sidder fast på den mindste cirkel. Når den mindste cirkel ruller inden i den næstmindste beskriver det sorte punkt den blå tandform. Og når den mindste cirkel ruller uden på den største beskriver den tandformen på det store tandhjul. Tændernes form er altså stykker af epicykloider. Det er en type kurver, der har været kendt siden græsk oldtid. En nærmere forklaring findes på vores side om Rømers tandhjul, der er link for oven.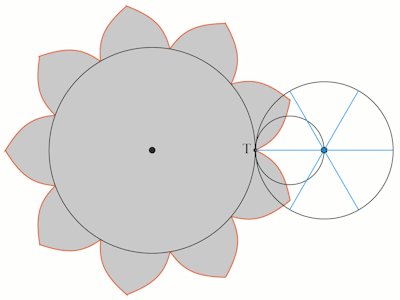

Hvis du er interesseret i at se en omhyggelig oversættelse af Eulers tekst om eksempel 1, så klik her.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.