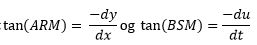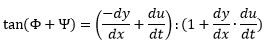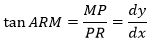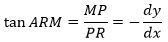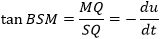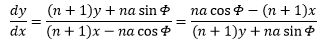Forside Søgning Liste

Eulers Første Tandhjulsartikel

Den 12. marts 1753 fremlagde Euler sin første tandhjulsartikel for Akademiet i St. Petersborg. I første søjle i tabellen nedenfor viser vi en oversættelse til dansk af Eulers artikel. I anden søjle er der kommentarer til artiklen. Den originale tekst på latin kan ses på adressen

https://math.dartmouth.edu/~euler/pages/E249.html

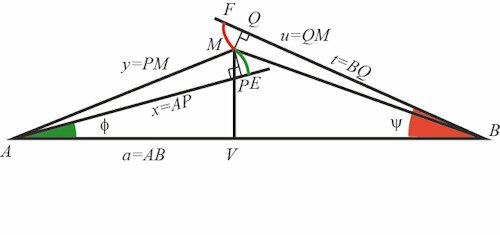
299 Om en Velegnet Form på Tænderne på Tandhjul. Forfatter L. Euler. Når et tandhjul i en maskine drives af et andet tandhjul, så plejer man at kræve at følgende to betingelser er opfyldt: For det første skal det være sådan, at når de ene tandhjul bevæger sig jævnt, så bevæger det andet tandhjul sig også jævnt. For det andet skal det være sådan, at under tændernes bevægelse opstår der ingen gnidningsmodstand. For at opnå at disse betingelser bliver opfyldt henvises til Fig 2. Lad A og B være rotationscentre for to tandhjul, hvor det ene drejer det andet rundt, og lad EM og FM være tænder, der rører hinanden i punktet M. Efter at de rette linjer AE og BF er ført til spidserne af begge tænderne, så sæt AB=a, vinklen BAE=Φ og vinklen ABF=Ψ. Mens hjulet med centrum A gør én omdrejning, så lad hjulet med centrum B gøre n omdrejninger, og på grund af begge bevægelsers ensartethed vil dΨ = n dΦ. Fremdeles fra kontaktpunktet M tegnes de vinkelrette MP og MQ og ligeledes tegnes fællestangenten SMRT og vi sætter: AP=x; PM=y; BQ=t og QM=u.	Jævnt betyder med konstant vinkelhastighed, og uden gnidningsmodstand betyder at tandhjulene skal rulle på hianden. Man kan matematisk bevise, at der ikke findes to tandhjul, hvor begge betingelser er opfyldt. Kort fortalt er argumentet følgende: I vore dage er der en kendt matematisk sætning, der siger, at hvis to sammenfaldende planer bevæger sig i forhold til hinanden, så kan bevægelsen på en og kun én måde beskrives ved, at en kurve i den ene plan ruller på en kurve i den anden plan. Se referencerne for at få en kilde. Hvis to tandhjul med centre C1 og C2 begge bevæger sig med konstante vinkelhastigheder, henholdsvis h1 og h2, vil deres planers bevægelse kunne beskrives ved en rulning på følgende måde: Tegn en cirkel i hver plan. Cirklerne skal have centre i tandhjulenes centre og og de skal begge gå gennem det punkt P på centerlinjen, der ligger sådan at PC1/PC2 = h2/h1. Under bevægelsen vil disse cirkler rulle på hinanden, og så kan tandhjulene ikke også rulle på hinanden. Eulers konklusion på side 301 er altså korrekt. Det der foregår, er at M ligger fast og de to linjer AP og BQ starter med at gå gennem M og dernæst drejer sig så Ψ vokser og Φ aftager. E og F starter i M. Afstandene AE og BF er varierende. Den røde kurve er banekurven for F og den grønne kurve er banekurven for E.
300 Efter at den vinkelrette MV er nedfældet fra M på AB får vi AV = x cos Φ - y sin Φ; MV = x sin Φ + y cos Φ BV = t cos Ψ + u sin Ψ; MV = t sin Ψ - u cos Ψ Herfra får vi t cos Ψ + u sin Ψ = a - x cos Φ + y sin Φ t sin Ψ - u cos Ψ = x sin Φ + y cos Φ Ud fra disse ligninger får vi t = a cos Ψ - x cos(Φ + Ψ) + ysin (Φ + Ψ) u = a sin Ψ - x sin(Φ + Ψ) - ycos (Φ + Ψ) Dernæst vil det på grund af den fælles tangent gælde at , og det følger af, at og da vil gælde, at ATM = ARM - Φ = BSM +Ψ hvoraf tan (ARM - BSM) = tan (Φ + Ψ) og ligeledes For at der ikke skal ske nogen gnidning, så er det kort sagt nødvendigt at buernes sum FM + EM = const. 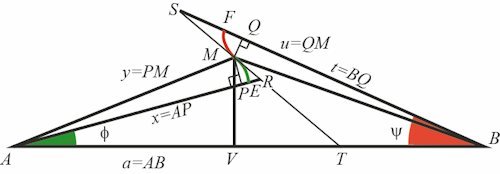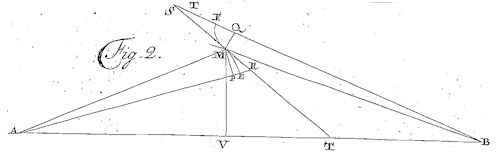eller √(dx2 + dy2) + √(dt2 + du2) = 0 og ligeledes dx2 + dy2 = dt2 + du2 Af den grund vil dt = -na dΦ sinΨ + (n + 1) x dΦ sin(Φ+Ψ) + (n + 1)y dΦ cos(Φ+Ψ) -dx cos(Φ+Ψ) +dy sin(Φ+Ψ) du = na dΦ cosΨ - (n + 1) x dΦ cos(Φ+Ψ) + (n + 1)y dΦ sin(Φ+Ψ) -dx sin(Φ+Ψ) -dy cos(Φ+Ψ)	Her har vi så tegnet fællestangenten ind på en ny figur. Den røde og den grønne kurve har en fællestangent i M, de to kurver er nemlig formen på tandhjulstænder. Alle de trigonometriske udregninger ned til formlen for PR er korrekte og lette for læsere, der kan deres trigonometri. Euler bruger f.eks. dy som betegnelse for den tilvækst, som y har fået siden starten, hvor y var 0. Så dy=MP. I formlerne for PR optræder der nogle uventede minusser. De forklares sådan: Fra starttidspunktet giver vi ψ en lille tilvækst; den ses på figuren og regnes positiv. Af figuren fås i første omgang men da vinklen aftager når tiden går, må det være sådan, at På tilsvarende måde fås, at Her udnyttes gnidningsbetingelsen.
301 Altså giver de nævnte ligninger (dx2 + dy2)sin(Φ+Ψ) = - na dΦdysinΨ + dxcosΨ) + (n + 1)dΦ(x dy -y dx)sin(Φ+Ψ) + (dx2 + dy2)sin(Φ+Ψ) + (n + 1)dΦ(x dx + y dx)cos(Φ+Ψ) (dx2 + dy2)cos(Φ+Ψ) = na dΦdxsinΨ -dycosΨ) - (n + 1)dΦ(x dx + y dy)sin(Φ+Ψ) + (dx2 + dy2)cos(Φ+Ψ) + (n + 1)dΦ(x dy - y dx)cos(Φ+Ψ) Ogsåledes får vi ved division med dΦ følgende to ligninger na / (n + 1) (dy sinΨ + dxcosΨ) = (x dy - y dx)sin(Φ+Ψ) + (x dx + y dy)cos(Φ+Ψ) na / (n + 1) (dy cosΨ - dxsinΨ) = (x dy - y dx)cos(Φ+Ψ) - (x dx + y dy)sin(Φ+Ψ) hvoraf vi når frem til følgende: x dy - y dx = na / (n + 1)(dy cosΦ + dxsinΦ) x dx + y dy = na / (n + 1)(dx cosΦ - dysinΦ) og heraf fremgår og ligeledes ((n + 1)y + na sinΦ)2 + ((n + 1)x - na cosΦ)2 = 0 hvilken ligning ikke kan tilfredsstilles med mindre man sætter y = na/(n+1) sinΦ og x = na/(n+1) cosΦ hvoraf følger u = a/(n+1) sinΨ og t = na/(n+1) cosΨ Og således vil det altså være for to tandhjul i indgreb, og af den grund kan det altså ikke ske, at begge de opstillede betingelser bliver opfyldt	Euler konkluderer her følgende: Man kan ikke opnå, at begge indledningsbetingelserne er opfyldt. Dette er korrekt, som vi skrev under side 299.
302 Men hvis vi altså negligerer gnidningsbetingelsen, så ville man nå frem til - na dΦ(dy sinΨ + dxcosΨ) cos(Φ+Ψ) + (n + 1)dΦ(x dy - y dx) = ?0? sin(Φ + Ψ) cos(Φ + Ψ) + (n + 1)dΦ(x dx + y dy) cos(Φ + Ψ)2 = ?0? - na dΦ(dx sinΨ - dycosΨ) sin(Φ+Ψ) - (n + 1)dΦ(x dy - y dx) = ?0? sin(Φ + Ψ) cos(Φ + Ψ) + (n + 1)dΦ(x dx + y dy) sin(Φ + Ψ)2 = ?0? eller na/(n+1)(dxcosΦ - dysinΦ) = xdx + ydy Når ligningen mellem x og y er givet vilkårligt, så vil både x og y kunne udtrykkes ved vinklen Φ og dermed kan den anden kurve mellem t og u blive bestemt	Såvidt jeg kan se konkluderer Euler her to ting: B. Hvis man ser bort fra gnidningsbetingelsen kan den ene tandkurve vælges vilkårligt, og dernæst kan den anden bestemmes entydigt. Denne påstand har jeg også set i moderne tekster, men med et lille forbehold som antyder, at der kan være forhold af ikkematematisk art, der blokerer for bestemmelsen af den anden kurve.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.
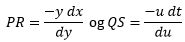