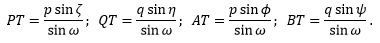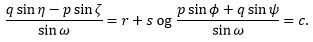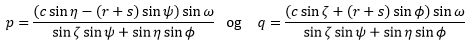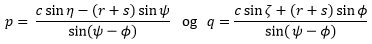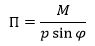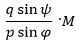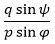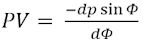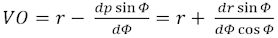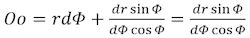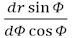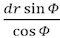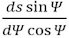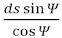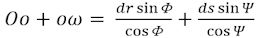| Ind til listen: |
Inddelingen i afsnit er Eulers, mens inddelingen i kapitler skyldes forfatterne af denne hjemmeside
Eulers supplerende artikel om formen på tænderne på tandhjul
Den 12. marts 1767 fremlagde Euler en supplerende tandhjulsartikel. Kapitelinddelingen her er ikke Eulers. I første søjle i tabellen nedenfor viser vi en oversættelse til dansk af Eulers artikel. Oversættelsen er ikke ordret. Mange steder har vi lavet ændringer og tilføjelser, også af figurer, der forhåbentlig gør det lettere for læseren. I anden søjle er der kommentarer til artiklen. Inddelingen i afsnit er Eulers. Den originale tekst på latin kan ses på adressen
http://eulerarchive.maa.org/
Søg på årstal 1762, E330
| Oversættelse til dansk | Kommentarer | ||
|
207 1. I dette fjerde bind af nye kommentarer fra Akademia Petropolitana angående formen på tænderne på tandhjul, har jeg fundet ud af at tilstrækkeligt dybtgående beregninger kan gennemføres på følgende måde, og derudfra har jeg opdaget, at løsninger tilpasset til praksis kan afledes derudfra. Jeg havde altså påvist, at enhver gnidningsmodstand ikke kan fjernes, når tænderne griber ind i hinanden, og yderligere kan det tilføjes, at når det ene hjul drejes jævnt, så kan man opnå, at det andet hjul påføres en jævn bevægelse: Hermed gælder samtidig følgende, nemlig at den kraft, som får det ene hjul til at rotere, den udløser vedholdende en lige så stor kraft til at føre det andet hjul rundt. På hvilken måde man altså bør formgive tænderne på begge de to hjul, det vil jeg udforske på følgende vis: Og eftersom det vil kunne udføres på uendelig mange måder, vil det være tilladt derudfra ganske frit at vælge den måde, der synes mest passende i praksis. |
Enhver gnidningsmodstand kan godt fjernes, hvis man ikke kræver konstant vinkelhastighed. Se et eksempel her på siden under 1675 Ole Rømer. Der er link øverst. Når Euler her skriver kraft mener han det, som vi i dag kalder moment. | ||
|
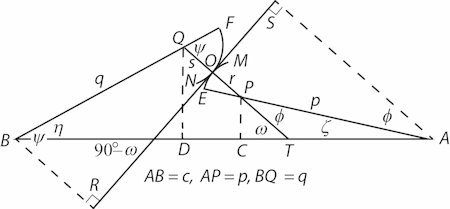
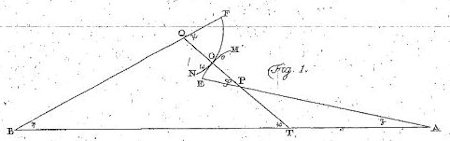
208 2. Lad A og B være centre for to tandhjul i indgreb, hvis afstand kan kaldes AB = c. Lad EOM være den bevægelige tand på hjulet med centrum A, og lad FON bevægelige tand på hjulet med centrum B som rører den anden tand i punktet O. På figur 1 oprettes normalen til de to tænder i punktet O. Den skærer de to radier i henholdsvis P og Q og den skærer den rette linje AB i T. Jeg antager nemlig, at punkterne E og F er i spidsen på begge tandhjul.
Fig. 1 Nu fastslår vi, at det første hjul bevæger sig således rundt om A, at vinklen BAE forøges. Så vil det andet hjul drejes således om B at vinklen ABF også forøges, og vi antager, at forholdet mellem disse to vinkler er konstant. |
I det meste af afsnit 2 beskriver Euler situationen på et vilkårligt tidspunket, hvor de to tænder EOM og FON rører hinanden i punktet O. Han finder en række relationer mellem afstande og vinkler, der gælder på ethvert tidspunkt. Euler går over til at studere bevægelsen i de sidste linjer af afsnit2. Forholdet mellem de to nævnte vinkler er lig med forholdet mellem antallene af tænder på de to tandhjul. | ||
|
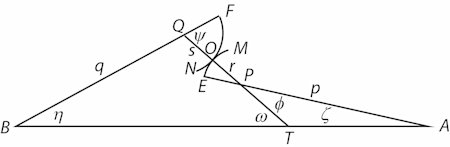
3. På figuren har vi vist følgende vinkler: BAE=ζ; ABF=η; EPO=Φ; FQO=Ψ og BTO=ω og heraf følger, at ζ = ω - Φ og η = Ψ - ω * Men vi sætter AB = c og yderligere AP = p; BQ = q; PO = r; QO = s. Herudfra følger af trekanterne APT og BTQ at 209 sin ω : p = sin ζ : PT = sin Φ : AT og sin ω : q = sin η : QT = sin Ψ : BT hvoraf følger
Da det gælder at QT - PT = r + s og AT + BT = c vil
hvoraf det udledes, at
Men ved indsættelse af * ovenfor fås, at sinζsinΨ + sinηsinΦ = sinω sin(Ψ - Φ), således at
|
Her i afsnit 3 benyttes det stadig ikke, at tandhjulene drejer 3 | ||
|
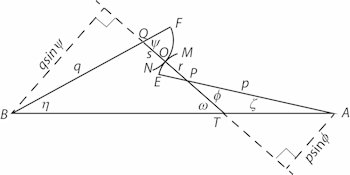
4. Lad Π være det tryk, med hvilket tænderne i punktet O påvirker hinanden. (Euler tænker på trykkets komposant på linjen QT) I begge retninger ligger trykket på linjen QT. Så vil momentet på hjulet A være M = Πp sinΦ, og på hjulet B vil det være Πq sinΨ. Vi antager nu, at det moment, der får hjulet med centrum A til at dreje om sit centrum er sådan, at vinklen ζ forøges og at momentet M er konstant. Hvis det andet hjul også drejer sig med konstant vinkelhastighed må det være påvirket af et konstant moment. Da
vil det moment, som det andet hjul drejes omkring B med være
og dette vil ske på den måde, at vinklen η forøges. Brøken
skal altså have en konstant værdi. Men så må forholdet mellem linjestykkerne AT og BT også være konstant nemlig AT:BT = psinφ:qsinψ . Ud fra dette vil punktet T være fast, sådan at AT´s forhold til BT er lig med forholdet mellem de momenter, der drejer A rundt og B rundt. |
I dag vil man betragte drejningsmomenter, som noget der skal afgøres i fysisk eller teknisk sammenhæng. At finde en form på tænderne i to tandhjul, der sikrer at begge tandhjul drejer sig med konstante vinkelhastigheder er ren matematik. Når tandhjulene er konstruerede kan de dreje sig uden ydre påvirkning. Det kommer som en overraskelse at Euler inddrager drejningsmoment i sine overvejelser. Det resultat, han kommer frem til, nemlig at den nævnte brøk er konstant, er korrekt. Euler nævner ikke direkte, at dette forhold er lig med forholdet mellem de vinkelhastigheder, som tandhjulene drejer sig med. Dette er den ene halvdel af en central sætning om tandhjul, som vi her på siden beviser under 1742 En sætning om tandhjul, der er link for oven. Jeg ved ikke hvem der først fandt denne sætning. | ||
210 5. Da RS = RO + OS (se Fig. 1) fås ved projektion på fællestangenten RS at (1) psinΦ + qsinΨ = csinω Ved projektion på QD fås, at (2) qsinη - psinζ = (r+s)sinω Der gælder endvidere følgende relationer mellem vinklerne (3) ζ = ω - Φ og (4) η = Ψ - ω Indsætter vi disse værdier i lignng (2), får vi: qsinΨcosω - qcosΨsinω - pcosΦsinω + psinΦcosω = (r+s)sinω
Fig. 1 Da første og fjerde led i ovenstående formel ifølge (1) er csinωcosω vil - qcosΨsinω - pcosΦsinω +csinωcosω = (r+s)sinω Ved at dividere med sinω får vi: - qcosΨ - pcosΦ+ccosω = r+s eller pcosΦ + qcosΨ = ccosω -r - s (5) På samme måde kan vi indsætte Φ = ω - ζ og Ψ = ω + η i ligning (1), og så får vi, at pcosζsinω - psinζcosω + qcosηsinω + qsinηcosω = csinω Her er andet og fjerde led ifølge (2) lig med (r+s)sinωcosω, så efter division med sinω får vi, at pcosζ + qcosη = c - (r+s)cosω (6) |
Ligningerne (5) og (6) benyttes på side 212b i kapitel 2. Der er intet om bevægelse på denne side. | ||
|
211a
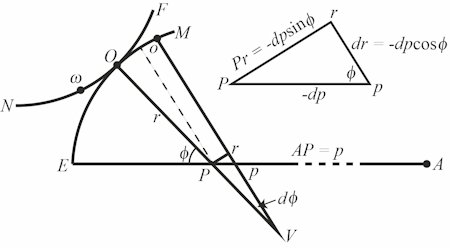
6.Udover disse resultater vil det være sådan, at der for kurven EOM vil være en sikker relation mellem de tre variable AP = p, PO = r og vinklen EPO = Φ, som her først og fremmest bør undersøges. (Den ligning, som Euler når frem til er en differentialligning, så nu er der en lillebitte bevægelse.) Lad os altså overveje den nærmere tilstand for størrelserne Ap = p + dp; po = r + dr og Epo = Φ + dΦ efter at normalerne OP og op er forlænget til skæring i V. Se figuren nedenfor, hvor den lille trekant Prp er tegnet i forstørret udgave for oven til højre. Euler har valgt at lade begge bogstaverne p og r have to betydninger, nemlig et punkt og et linjestykke. VO er radius for oskulationscirklen til tanden EOM i punktet O. Med centrum i V kan den lille bue Pr tegnes, og det gælder da, at Pp = -dp; pr = dr; Vinklen Ppr = Φ + dΦ og vinklen OVo = dΦ Sammenfattet gælder, at pr = dr = -dpcosΦ (dette er den differentialligning, som Euler annoncerede ovenfor), og Pr = -dpsinΦ og
(Denne formel vises ved at anvende sinusrelationen på trekant PpV, idet man kan regne med, at vinkel PpV = 180 - Φ og at sindΦ = dΦ.) Ud fra dette vil radius for oskulationscirklen være
Det første lighedstegn gælder fordi dp er negativ, og det andet lighedstegn følger af, at dp = -dr/cosΦ. |
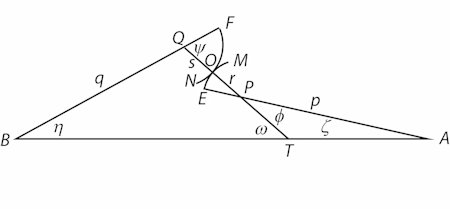
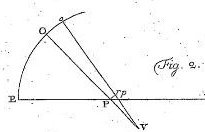
Euler går nu over til at undersøge gnidningshastigheden i et røringspunkt O mellem tænderne. Figur 2 til venstre er ikke Eulers. Han har i stedet nedenstående figur
Som vist på side 209 ligger dette punktet T fast, når tandhjulene drejer sig, hvis de begge drejer sig jævnt. Som nævnt på side 208 vokser vinklen BAE når tiden går. Nu går Euler over til at bruge differentialregning. Bogstavet d betyder "tilvækst på". I moderne matematik bruges betegnelsen Δ. Euler tager udgangspunkt i en vilkårlig beliggenhed af O. Så venter vi et meget kort øjeblik. O flytter sig så hen til punktet o. På figuren er den vandrette linje linjen AP og Euler har tegnet de to normaler til EOM ind. De skærer hinanden i V. p bliver så en smule mindre, så tilvæksten dp bliver negativ. Euler skriver Pp = -dp fordi Pp er et linjestykke, der altid regnes positivt. Vinkel EPO = Φ, og vinklen nede ved V-et er dΦ, som er positiv. | ||
|
211b
6. fortsat. På figuren ovenfor er det punkterede linjestykke parallelt med or. Derfor gælder det, at Oo = rdΦ + Pr = rdΦ -dpsinΦ. Resultatet er, at
(Hvis man multiplicerer størrelsen mellem de to lighedstegn med dΦ bliver 1. led kvadratet på en uendelig lille størrelse, mens det andet led bare bliver uendelig lille. Derfor kan man droppe rdΦ) Radius i oskulationscirklen for kurven EM i O er
(Her burde Euler have skrevet udtrykket for VO.) Linjestykket Oo er
(Her burde Euler have skrevet udtrykket for Oo.) Da tilsvarende formler gælder for den anden tand, har vi ialt følgende resultater: ds = -dqcosΨ; radius i oskulationscirklen for kuven FN i O er
(Her burde der adderes sdΨ) Linjestykket Oω er
(Her er ω det punkt, der svarer til o, det har ikke noget med vinklen ω at gøre. Og der er samme fejl som ovenfor) På Eulers figur nedenfor kan man se beliggenheden af punkterne o og ω
| Oskulationscirklen for en kurve i et punkt O er den cirkel, der i en lille omegn af O er nærmest ved at falde sammen med kurven. (Osculor på latin betyder kysser,
så vores latinkyndige oversætter undrede sig over, at der var så meget kysseri i en matematisk tekst!)
Euler har skrevet nogle fejl her i afsnittet om gnidning. Men resultatet er formodentlig ikke særlig betydningsfuldt, hvis man i praksis vil reducere gnidningen. Metoden til at bestemme den lokale gnidning er rigtig nok. | ||
|
7. Da nu tænderne berører hinanden i punktet O, vil efter kort tids forløb o og ω nærmer sig O så er det tydeligt at gnidningen sker på strækningen oO + ωO således at hele gnidningsforløbet vil være
Men tidsrummet for gnidningen kunne føres tilbage til intet, og så fjernes hele gnidningen. Men i den forudgående afhandling har jeg vist, at dette ikke kan lade sig gøre. Der vil altså altid være gnidning, og gnidningen vil være større jo større værdi formlen har. 212a Altså vil det altid forholde forholde sig på følgende måde: Den gnidning, der sker, vil være større, jo større følgende værdi er:
Thi hvad angår størrelsen af gnidningen så er den proportional med det gensidige tryk mellem tænderne, og det tryk betegner vi nu Π. Gnidningstilvæksten betegner vi nu δΠ. Da denne er normal til OP, vil dens moment på hjulet A være δΠ(r + pcosΦ) (se 2. figur på side 209) | Jeg synes, at Euler burde have fundet gnidningshastigheden i punktet O. Resultatet er såvidt jeg kan se ikke af særlig betydning. |