Mere om Eulers tandhjul

1. Indledning

Omkring 1675 foreslog Ole Rømer en bestemt form for tænderne i et tandhjul. Den form beskrives udførligt her på hjemmesiden under Rømer i 1675. Formålet med Rømers tandhjul var at sikre, at når det ene af to tandhjul i indgreb bevæger sig med konstant vinkelhastighed, da vil det andet også bevæge sig med konstant vinkelhastighed. Tandhjul med denne egenskab kalder vi her "jævne". Med jævne tandhjul undgår altså de små variationer af vinkelhastigheden ved passage af hver enkelt tand, der vil finde sted, hvis man bruger tilfældige tandformer. Man kan også sige, at to tandhjul er jævne, når forholdet mellem deres vinkelhastigheder er konstant, mens tandhjulene drejer sig.

Omkring 1750 fandt Euler en anden tandform, der også sikrer konstant vinkelhastighed. Jeg har ikke haft fuld adgang til Eulers egen beskrivelse, men i 1767: Eulers artikel om tandhjul dokumenterer jeg, at det, Euler fandt på, er det, som beskrives nedenfor.

2. Cirkelafvikleren

De kurver, der begrænser en tand i et af Eulers tandhjul, er små stykker af de kurver, der hedder cirkelafviklere. Dem beskriver vi nu nærmere.

De 5 billeder ovenfor viser en lav cylinder, som der tegnet et kryds oven på. Som man kan se, drejer cylinderen sig ikke, og den sidder fast på et cirkelformet underlag. Der er viklet en snor rundt om cylinderen, og den ender i et lille øje, som der er stukket en blyantsspids ned i. På figuren længst til venstre holder blyantsspidsen snoren stramt ind på cylinderen. Derefter føres blyantsspidsen med stram snor langsomt væk fra cylinderen, og under bevægelsen tegner blyanten en kurve på underlaget. Det er sådan en kurve, der kaldes en cirkelafvikler. Kurven fortsætter i en spiral rundt om cylinderen, men som vi skal se, får vi her kun brug for det stykke af afvikleren, der ligger ret tæt på afviklerens begyndelsespunkt. Afviklerens form er bestemt af cylinderens radius. På figurerne nedenfor viser vi afviklerne for to cirkler, hvis radier forholder sig som 2 til 3.

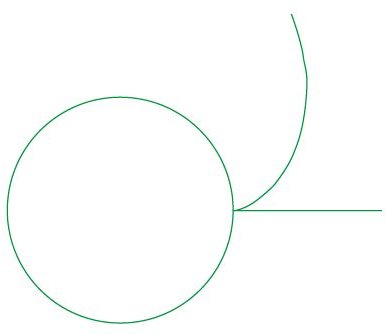Man kan vise, at en afviklers tangent i begyndelsespunktet er vinkelret på cirklens tangent i samme punkt. Mere generelt kan man vise, at når snorens øje er nået til et bestemt punkt af afvikleren, da er afviklerens tangent i dette punkt vinkelret på snoren. Beviset findes her

En afvikler krummer mindre og mindre, når man fjerner sig fra dens begyndelsespunktet.

I stedet for at lade cylinderen være fast og lade snoren dreje sig, lader vi nu cylinderen og underlaget dreje sig med uret om det ubevægelige centrum, og med blyanten holder vi hele tiden snoren stram og vandret. Vi starter til venstre på figurerne nedenfor. Pointen er nu, at når vi bevæger os mod højre så vil blyanten igen tegne afvikleren, denne gang på det roterende underlag. Snoren bliver igen viklet af cylinderen. Man kunne forestille sig, at cylinderen ruller på en vandret linje under cylinderen.

Billederne ovenfor kan også læses fra højre mod venstre. Så vil cylinderen rotere mod uret og snoren vil blive viklet op på cylinderen. Hvis afvikleren ikke var der i forvejen vil den igen blive tegnet af blyanten, denne gang udefra og ind mod cylinderen. Man kunne kalde det en påvikler, men det gør man ikke.

3. Eulers tandhjulskonstruktion

Et par af kurver, der kan dreje sig om hver sit omdrejningspunkt, kalde jævne, hvis det er sådan, at hvis den ene kurve drejes jævnt (dvs. med konstant vinkelhastighed) og hele tiden rører ved den anden, så drejer den anden sig også jævnt. I vores omtale af Rømers tandhjul har vi beskrevet en række jævne kurvepar. Animationen til venstre viser et eksempel. Det, der foregår, er følgende: Der er et sort punkt, der bevæger sig jævnt rundt på den lille grønne cirkel og så er der to farvede planer. En blå, der drejer sig om den øverste cirkels centrum, og en rød, der drejer sig om den nederste cirkels centrum. Der sorte punkt tegner den blå kurve i den blå plan og den røde kurve i den røde plan. Rømer beviste så, at den blå og den røde kurve er et jævnt kurvepar, når vinkelhastighederne er valgt på en bestemt måde - som på animationen. -Og, kære læser, det vil lette din forståelse af det følgende, hvis du har forstået denne beskrivelse.

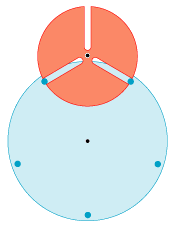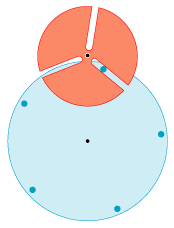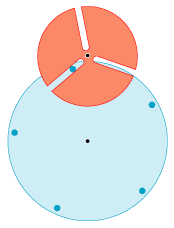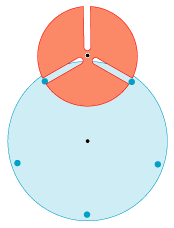
På animationen til højre viser vi et par tandhjul, der absolut ikke er jævne. Det blå tandhjul har 5 tænder, der er korte cylindre, der er vinkelrette på tandhjulets plan. Der røde tandhjul har tre brede tænder. Mellem tænderne er der smalle retlinede kanaler. Bredden af kanalerne er lig med de blå cylindres diameter. Det blå tandhjul drejer sig jævnt, og som man kan se, bevirker det store variationer i det røde tandhjuls vinkelhastighed. Det er let at gøre det meget bedre, men det viser sig, at det at konstruere jævne tandhjul kræver differentialregning oven i særdeles gode ideer.

Vi går nu over til at beskrive Eulers jævne tandhjul. Vi vælger at beskrive et konkret eksempel, hvor forholdet mellem vinkelhastighederne er som 2 til 3, men princippet kan bruges uanset forholdet mellem vinkelhastighederne. At Euler fosreslog at bruge tandhjul, hvis tænder er formet som involutter kan vi dokumentere med en artikel, som Euler skrev i 1767, og som vi bringer uddrag af på vores side om Eulers artikel. Se linket for oven, og gå ned til slutningen af artiklen.

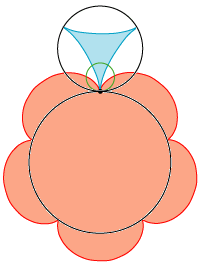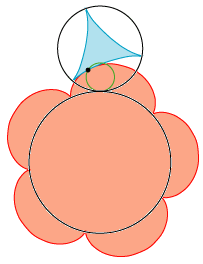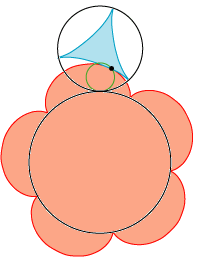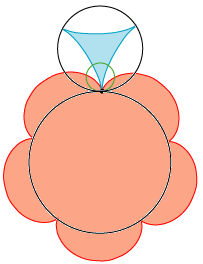
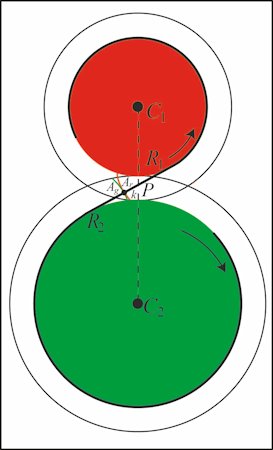
På billedet til venstre viser vi udgangspunktet. Den røde cirkel er den centrale del af et tandhjul med 12 tænder, og den grønne cirkel er den centrale del af et tandhjul med 18 tænder. Forholdet mellem de to cirklers radier er som 2 til 3. Cirklerne roterer i pilenes retning med vinkelhastigheder, der forholder sig som 3 til 2. Det bevirker, at cirklernes periferier bevæger sig lige hurtigt. Afstanden mellem de to cirkler er valgt nogenlunde tilfældigt. Afstanden er tændernes udstrækning i radiær retning, så den skal vælges fornuftigt. Der er en sort snor. Den er viklet et stykke rundt om den røde cirkel. Snoren fortsætter stramt i R1 som den skrå, sorte linje, der er fællestangent til de to farvede cirkler. Fra R2 er snoren viklet op om den grønne cirkel. Snorens to ender er sat fast på cirklerne. Snoren skal være stram. Vi tænker os nu, at de to cirkler roterer i pilenes retning med vinkelhastigheder, der forholder sig som 3 til 2. En lille udregning viser, at så vil snoren hele tiden være stram. Der er slået en knude k på snoren. Den følger med snorens bevægelse. Snoren skærer skærer den punkterede centerlinje i punktet P. P deler centerlinjen C1 C2 i radiernes forhold. De to sorte cirkler angiver hvor langt ud tænderne skal gå. Nu tænker vi os at der ud over den faste plan er to bevægelige planer, der falder sammen med den faste plan. Der er en rød plan, der roterer om C1. Den er kun tegnet rød inde i den øverste cirkel. Og der er en grøn plan, der kun er tegnet grøn inde i den nederste cirkel. De to planer roterer ligesom cirklerne. Vi tænker os nu, at knuden k bevæger sig fra R2 til R1 og at den under denne bevægelse tegner sine banekurver både i den røde plan og i den grønne plan. Banekurven i den grønne plan er en afvikler Ag, til den grønne cirkel, som starter i R2, vinkelret på cirklen. Ag er tegnet ind i startsituationen. Banekurven i den røde plan er en påvikler Ar, til den røde cirkel, som slutter i R1, vinkelret på cirklen. Ar er tegnet ind i slutsituationen. For begge banekurver gælder det, at der kun er tegnet den del, der ligger inde i den tilsvarende sorte cirkel. I det følgende betegner Ag og Ar disse korte kurver. Figuren kan virke misvisende, fordi kurverne er tegnet til forskellige tidspunkter.

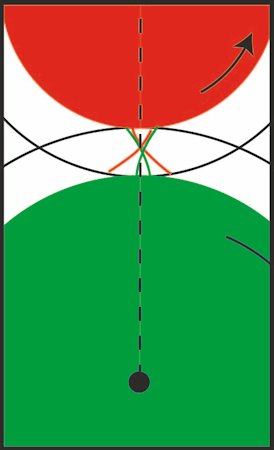
Vi tænker os nu, at knuden har gennemløbet hele strækningen, så de to banekurver Ag og Ar er tegnet færdigt. På figuren til højre kigger vi så på situationen på et vilkårligt tidspunkt. Vi har drejet de to banekurver så de begge går igennem k. Da kurvernes tangent i punktet k begge er vinkelrette på snoren, og da kurverne krummer hver sin vej, rører kurverne hianden i k og vi kan så beskrive bevægelsen på en anden måde: Vi tænker os at Ag er sat fast på den grønne cirkel og Ar er sat fast på den røde cirkel og at bevægelsen vedligeholdes ved at Ag skubbber til Ar. Da begge vinkelhastigheder er konstante, er bevægelsen jævn. Hermed har vi i det væsenlige løst opgaven: Nemlig at finde en tandform, der giver en jævn bevægelse. Der mangler bare en række mindre ting, som vi nu går over til at beskrive. Det, der er Eulers bedrift, er dels at få den ide at bruge afviklere og - mere imponerende - at bruge den snor med knude til samtidig at finde en tandform på det ene tandhjul og den tilsvarende tandform på det andet tandhjul. Bemærk, at tandformerne ikke er ens, de er afviklere til forskellige cirkler.

Nu har vi konstrueret den ene side ef en grøn og en rød tand. Nu går vi over til at konstruere den anden side af disse to tænder. Det kunne man gøre på den måde, at man gentog processen ovenfor med den ændring, at snoren følger den anden fællestangent for de to cirkler. Resltatet vil blive et spejlbillede i en lodret linje af det, vi fik ovenfor. Vi konstruerer nu dette spejlbillede. Det gør vi på den måde, at vi først tegner den beliggenhed, som kurverne vil have, hvis k befinder sig i det punkt P, som vi nævnte ovenfor, og så spejler dem i den lodrette linje gennem centrene. Resultatet er vist på figuren til venstre.

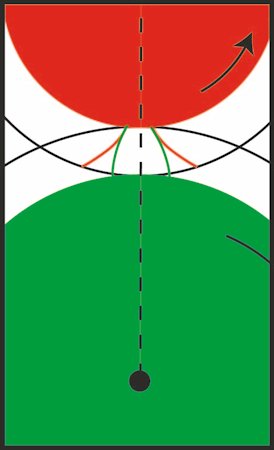
Så skal vi bestemme bredden på tænderne. Der er ingen teori, der udtaler sig om, hvad den skal være, kun sund fornuft. Vi vælger at dreje de 2 røde kurver hver 6° væk. Så skal de grønne kurver drejes 4° væk. Resultatet kan ses på figuren til højre. Her ses den grønne tand tydeligt. De røde kurver tilhører hver sin tand, nemlig nabotænderne til den grønne tand. Der er 30° mellem to røde nabotænder. Så for at få to røde kurver på samme tand drejer vi den røde kurve til højre 30° med uret. Så får vi to sider af en rød tand.

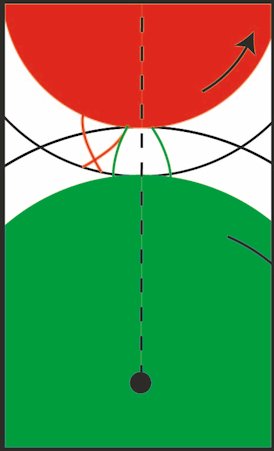De to sider skærer hinanden, så vi er nødt til at skære lidt af de to røde kurver. Måske kunne man undgå denne detalje ved at ændre på tandbredden og eller ændre afstanden mellem de to tandhjul. Teknisk set kan det være vigtigt, men teoretisk er det ikke vigtigt. Tandhjulene er stadig jævne.

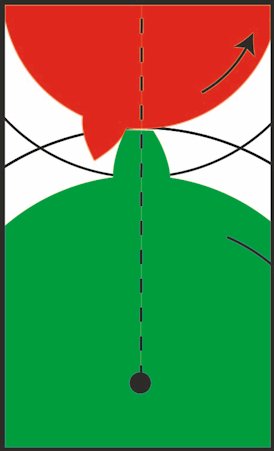
Og nu har vi så to nabotænder, der rører hinanden. De andre 11 røde tænder får vi ved at kopiere den røde tand og dreje kopien 30° - og så gentage denne proces 11 gange. De andre 17 grønne tænder får vi ved at kopiere den grønne tand og dreje kopien 20° - og så gentage denne proces 17 gange.

Til venstre viser vi så de to færdige tandhjul, og til højre lader vi dem dreje rundt.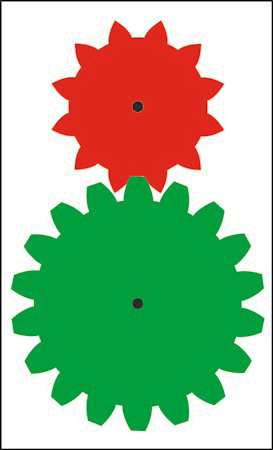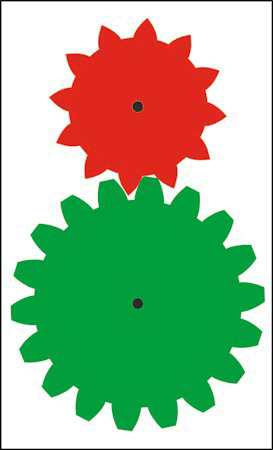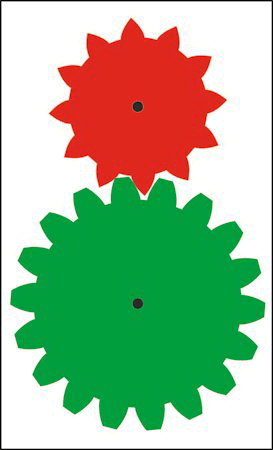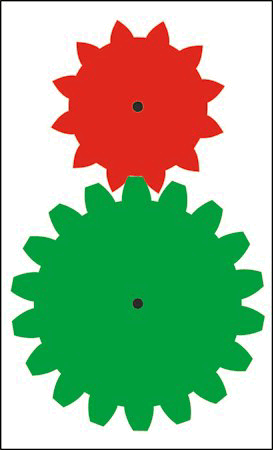

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.