Bestemmelse af tangenter til en afvikler

Det vi vil bevise, er at hvis P er et punkt på afvikleren til en cirkel, så vil afviklerens tangent i P være vinkelret på QP, som er snorens stilling, i det øjeblik den passerer P. For at finde tangenten vil vi først finde en parameterfremstilling for afvikleren. Som parameter bruger vi vinklen t fra X - aksen til vektoren OQ. Vinklen t skal måles i radianer, så opnår vi, at både cirkelbuen fra X - aksen og op til Q og vektoren QP har længden rt. I udregningen nedenfor bruger vi at cos(t - 90°) = sin t og at sin(t - 90°) = -cos t.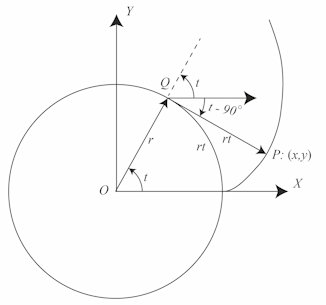

Vi går nu over til at finde parameterfremstillingen for afvikleren. Idet koordinaterne til P kaldes (x,y) skal vi finde x og y som funktioner af t:

(x,y) = OQ + QP = r(cos t, sin t) + rt(sin t, - cos t).

Tangentretningen findes heraf ved differention mht t under brug af produktreglen:

(dx/dt, dy/dt) = r(- sin t, cos t) + r(sin t, - cos t) + rt(cos t, sin t) = rt(cos t, sin t).

Her gik de to første led ud mod hinanden, og tangentens retning er derfor bestemt af vektoren (cos t, sin t). Tangenten i P er altså parallel med OQ og derfor vinkelret på QP.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.