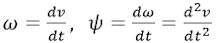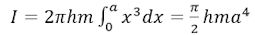Forside Søgning Liste

1. Inertimoment

I den grundlæggende bevægelseslære betragter man normalt først bevægelsen af et punktformet legeme P med masse m, og så studerer man hvordan P bevæger sig under påvirkning af forskellige ydre kræfter. Vilkårene skifter meget, når vi nu går over til at betragte et legeme L, der kan dreje sig om en akse. Det vi skriver her skal ses i fortsættelse af det, som vi skrev under 1780 Arbejde og energi, se link foroven.

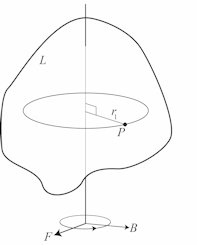Figuren viser legemet L, der kan dreje sig om den lodrette akse. Hvert enkelt punkt af aksen ligger fast, og hvis der er punkter af L, der ligger på aksen, ligger de også fast. Forneden er der en lille ellipse med en pil. Den viser, hvilken vej drejningen regnes positiv. F forneden er en fast retning, mens B bevæger sig rundt sammen med legemet. Til et begyndelsestidspunkt falder B sammen med F, og når legemet har drejet sig v radianer er vinklen fra F til B v radianer. Legemets øjeblikkelige vinkelhastighed ω er det antal radianer pr. sekund, som legemet drejer sig med. Og legemets øjeblikkelige vinkelacceleration ψ er det antal radianer pr. sekund som vinkelhastigheden ændrer sig med. For dem, der kan differentiere, kan det formuleres således:

Nu går vi over til at bestemme den kinetiske energi af legemet, på et tidspunkt hvor vinkelhastigheden er ω. Vi tænkes os legemet opdelt i en mængde små dele, og vi bestemmer så legemets kinetiske energi som summen af de energier, som de enkelte massedele har. Lad os sige, at en massedel med masse m₁ befinder sig i punktet P på figuren ovenfor. P ligger inde i legemet, og ellipsen forestiller den cirkelformede bane, som P beskriver under bevægelsen. Så har denne partikel hastigheden r₁ω (se evt. -1000 Vinkelmål) og derfor bliver dens kinetiske energi ½m₁r₁²ω². Tilsvarende udtryk fås for de andre massedele masser m₂, m₃, m₄, ···, og legemets samlede kinetiske energi bliver derfor

E = ½m₁r₁²ω² + ½m₂r₂²ω² + ½m₃r₃²ω² + ··· = ½(m₁r₁² + m₂r₂² + m₃r₃²+ ···)ω² = ½Iω²

Her har vi sat I = m₁r₁² + m₂r₂² + m₃r₃²+ ··· , og dette tal kaldes legemets inertimoment. Udtrykket ovenfor minder på en interessant måde om udtrykket e = ½mv² for en partikels kinetiske energi idet E svarer til e, I svarer til m og ω svarer til v.

Inertimomenter kan være svære at beregne. Vi illustrerer beregningen med et eksempel, som er er en forudsætning for Coulombs vigtige elektriske målinger. Vi vil bestemme inertimomentet I for den cylinder, der er vist på figuren til højre. Cylinderen er lavet af et metal, der har vægtfylde m; radius er a, og cylinderens højde er h. Cylinderen kan dreje sig om den lodrette linje gennem endefladernes centre. Figuren viser også en tyndvægget rørformet cylinder C. Rørets diameter betegnes x og vægtykkelsen er dx. Man kan regne med, at alle punkter i C har afstanden x fra aksen. Derfor er det let at beregne det bidrag dI til I, som C giver: Rumfanget af C er 2πx·dx· h. Derfor er dI = x2 · 2πx·dx·hm = 2πhm· x3dx. Og så kommer man ikke uden om at lave en integration:

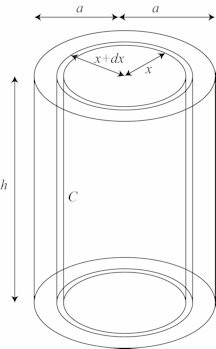Da vægten af cylinderen er M = πa²hm kan inertimomentet for cylinderen også bestemmes af formlen I = ½Ma².

Inertimomentet er et mål for, hvor svært der er at få legemet til at rotere om aksen. Hvis man øger a til det dobbelte, så bliver M multipliceret med 4 og inertimomentet bliver 16 gange så stort!

20 år efter at Euler havde beskrevet begrebet inertimoment, blev det vigtigt for Charles Augustin Coulomb, der som den første målte meget svage elektriske kræfter.

Ovenfor viser vi de 4 linjer fra Coulombs originale publikation, hvor han udleder det samme inertimoment, som vi lige har fundet. ∫πr² er Coulombs betegnelse for inertimoment, (her betyder π ikke π = 3,1415 ...) og han skriver bare, at man finder den brøk, der har 4 i nævneren. L er cylinderens højde, δ er vægtfylden, og så skriver han mærkeligt nok, at φ er forholdet mellem omkreds og radius, hvilket er 2π. Gad vist hvorfor han ikke skriver det? Resultatet er korrekt. De to 4-taller i resultatet kan Coulomb kun have fundet ved at udføre en integration.

Vi går nu over til at bestemme inertimomentet I af stangen på figuren ovenfor. Der er tale om en vandret stang med en lille kugle i hver ende. Stangen kan dreje sig om den lodrette akse gennem stangens midtpunkt. Stangens længde er 2l, dens vægt er 2m og kuglernes vægte er m₁ og m₂.

Vi starter med at betragte et punkt på stangen, der ligger i afstanden x fra dens midtpunkt. Vi giver nu x en lille tilvækst dx. Så får I tilvæksten dI = m/l·x². Nu kan det samlede inertimoment findes ved integration:

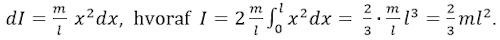
Hertil skal så lægges kuglerne bidrag til inertimomentet for hele legemet, som er l(m₁² + m₂²).

Som vi skal se under vores beskrivelse af Coulombs målinger, var dette resultat af afgørende betydning for Coulomb. -Der er link foroven.

For at sikre jævn gang skulle dampmaskiner i gamle dage være forsynet med et svinghjul med stort inertimoment. Svinghjulet på denne gamle spanske dampmaskine har med god tilnærmelse inertimomentet I = MR2, hvor M er hjulkransens masse og R er hjulets radius	- og her er så en russisk maskine med et inertimoment, der vil noget

2. Drejningsmoment

I vores omtale af inertimoment har vi bestemt den kinetiske energi i et legeme, der drejer sig om en akse. Vi går nu over til at beskrive virkningen af kræfter, der påvirker et roterende legeme. En kraft der er parallel med aksen har ingen indflydelse på legemets bevægelse. Det samme gælder om en kraft der ligger på en linje, der skærer aksen. Vi kan derfor nøjes med at betragte kræfter, der er vinkelrette på aksen, og som ikke ligger på en linje, der skærer aksen.

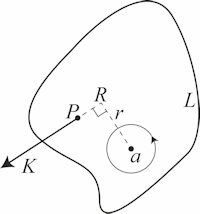
På figuren til venstre er omdrejningsaksen a vinkelret på skærmen. Legemet L er påvirket af en enkelt kraft K, og legemets inertimoment betegnes I. Afstanden fra a til den linje kraften ligger på kaldes r. Produktet H = Kr kaldes kraftens moment, og det har været kendt siden oldtiden, at det er momentet, der bestemmer kraftens virkning. Det følger heraf, at en kraft ikke ændrer sin virkning på legemet, når man forskyder kraftens angrebspunkt til et andet punkt på den linje, som kraften ligger på. Se vores artikel om vægtstangen, der er link foroven. Momentet regnes med fortegn på den måde, at momentet er positivt, når det prøver at dreje legemet den vej, som pilen nede ved a drejer. På figuren er momentet altså positivt, men hvis kraften pegede den anden vej, ville momentet være negativt. Momentet bevirker en ændring af den øjeblikkelige vinkelhastighed ω. I et kort tidsrum fra tidspunktet t til tidspunktet t + Δt ændres vinkelhastigheden fra ω til ω + Δω. I dette korte tidsrum er den kinetiske energi vokset med værdien

½I(ω + Δω)² - ½Iω² = ½Iω² + Iω Δω + ½I(Δω)² - ½Iω² = Iω Δω + ½I(Δω)² = Iω Δω. Her kan Δω godt være negativ.

Her har vi set bort fra leddet med (Δω) ² fordi det er enormt lille i forhold til Iω Δω. Resultatet er, at på Δt sekunder er den kinetiske energi steget med værdien Iω Δω.

Vi går nu over til at beregne det arbejde, som kraften K udfører i de samme Δt sekunder. Vi kan som nævnt antage, at kraften K angriber legemet i det punkt, som R befinder sig i til tidspunktet t. I tidsperioden fra t til t + Δt vil punktet R bevæge sig et stykke i retning af K. Da vinkler måles i radianer (se Vinkelmål, der er link for oven), vil det stykke, R bevæger sig være rωΔt. Derfor vil det arbejde, som Kraften udfører i disse Δt sekunder være K·rωΔt. Da arbejdet er lig med tilvæksten i energi har vi altså, at

K·rωΔt = Iω Δω

Hvis vi kalder drejningsmomentet Kr for H har vi altså, at

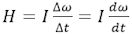
Denne formel er afgørende for den måling af elektrisk tiltrækning og frastødning, som Coulomb udførte i 1785.

Hvis legemet er påvirket af flere momenter, f.eks. H₁, H₂ og H₃ gælder ligningen ovenfor stadig,
når man sætter H = H₁ + H₂ + H₃.

Denne påstand svarer til at for en punktformet masse, der er påvirket af 3 kræfter, er summen af kræfterne masse gange acceleration. Jeg er ikke klar over, hvornår man første gang blev opmærksom på sådanne analogier mellem kræfter, der påvirker et massepunkt, og momenter, der påvirker et legeme, der kan dreje sig om en akse.