Forside Søgning Liste

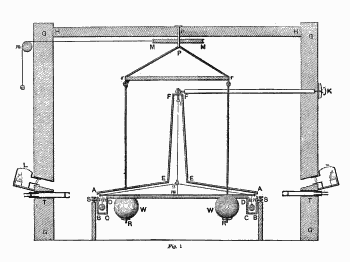
Om John Michells arbejder i fysik

John Michell (1724 - 1793) var en engelsk præst, der også arbejdede som fysiker og geolog. Michells arbejder var ikke særlig kendt på hans egen tid, men i dag er han velkendt blandt fysikere, især fordi han var den første, der indså muligheden af det, der i dag kaldes sorte huller.

Jeg synes nu, at det mest betydningsfulde arbejde, som Michell udførte, var hans konstruktion af et apparat, der kunne anvendes til bestemmelse af Jordens gennemsnitlige vægtfylde. Michell døde, inden han fik brugt apparatet. Apparatet blev så skilt ad, og det endte hos Henry Cavendish, der rekonstruerede apparatet og brugte det til at finde en overraskende præcis værdi af Jordens gennemsnitlige vægtfylde. Der er link til Cavendish foroven. Cavendish starter sin artikel med at meddele, at apparatet er konstrueret af Michell, og han bruger de to første siden af sin artikel på at beskrive Michelles konstruktion. Cavendishs eget bidrag til apparatet er især at han placerede det i et meget stabilt rum omgivet af tykke vægge og med solidt loft.

Til højre viser vi Cavendishs tegning af apparatet. Det står indendørs på et meget stabilt underlag. Yderst er der en kasse med ca 60 cm tykke vægge og loft. Apparatet er en snovægt, og det der bliver snoet, er en tynd messingtråd, der foroven er gjort fast mellem de to F-er på billedet. Tråden er ca. 1 meter lang, og forneden er den fastgjort på midten af en let vandret vægtstang af træ, der er 180 cm lang. Man kan ikke se vægtstangen tydeligt på billedet, men den går fra A til A. I hver ende af stangen hænger der en lille blykugle af, der vejer 725 gram. Vægtstangen er hele tiden vandret, og den kan dreje sig ca. 2° til hver side fra midterstillingn. Der er også ophængt to store vægte af bly. Som man kan se hænger de i en vandret stang, som man kan dreje udefra ved at trække i en snor, hvis to ender kommer ud af rummet for oven til venstre. Hver af vægtene vejer 158 kg.

Ideen er nu, at man først drejer den stang, som de store kugler hænger i, sådan at de er så langt som muligt fra de små kugler. Så venter man på, at vægtstangen er faldet til ro. Dernæst drejer man stangen, som de store kugler hænger i, så de kommer tæt på de små kugler. Så tiltrækker de store kugler de små , og derfor drejer stangen, som de små kugler hænger i, en lille bitte smule. Så bliver tråden som bærer vægtstangen snoet lidt. Ud fra det kan man beregne, hvor stor tiltrækningskraften er. Disse udregninger er beskrevet i vores artikel om Cavendishs eksperiment, der er link for oven.

Selv ganske svage luftstrømninger kan forstyrre bevægelserne. Derfor er vægtstangen, de små kugler og tråden indesluttet i en tyndvægget kasse af mahogni. Kassen kan ses på billedet til venstre. Der er to huller i kassen, et i hver ende. Det ene hul kan ses på billedet. På det øverste billede kan man se to lamper, der gennem linser kaster lys ind gennem hullerne. Neden under lamperne er der to teleskoper. Gennem dem kan man se, hvor mange grader vægtstangen drejer sig.

Jeg synes, at det er beundringsværdigt at Michell på denne måde kunne konstruere et apparat, som kunne måle de meget svage tiltrækningskræfter. Der er tale om kræfter ned til 0,01 mg, altså en hundrededel af et milligram!.

2. Om brug af statistik i astronomien

På Michells tid havde den matematiske statistik udviklet sig til et nyttigt hjælpemiddel i mange sammenhænge. Michell fandt i 1767 ud af, at hvis stjernerne var tilfældigt fordelt på himlen, så ville der være meget færre par af tilsyneladende tætliggende af stjerner, end man faktisk observerer. Han drog den konklusion, at disse dobbeltstjerner, som man kalder dem i dag, bliver holdt i nærheden af hinanden af den gensidige tiltrækningskraft og at de roterer omkring deres fælles tyngdepunkt.

Et af de astronomiske objekter som Michell beskæftigede sig udførligt med var Syvstjernen, i fagsprog Plejaderne. Med det blotte øje kan man nu kun se 6 stjerner. Problemet er følgende: Er det 6 stjerner i vidt forskellige afstande fra os som bare tilfældigvis ses i omtrent samme retning? Eller har disse 6 stjerner samme afstand fra os, og holdes de sammen af massetiltrækningen? Michell beregnede sandsynligheden for, at de tilfældigvis ses i samme retning. Han fandt at den er 1/500.000. Så han slog fast, at Plejaderne har samme afstand fra os, og at de holdes sammen af massetiltrækningen.

Plejaderne

3. Michells omtale af sorte huller i 1783.

På Michells tid var det kendt, der til ethvert himmellegeme er knyttet en undvigelseshastighed. Det er den begyndelseshastighed, som man i retning væk fra centrum er nødt til at give en lille partikel, hvis man vil opnå, at partiklen ikke falder ned igen.

Beregning af undvigelseshastigheden kræver, såvidt jeg ved, kendskab til gravitationskonstanten G i Newtons tiltrækningslov. Størrelsen af G var ikke kendt på Michells tid. Jeg tvivler derfor på, at Jordens undvigelseshastighed var kendt dengang. I dag er det kendt, at Jordens undvigelseshastighed er 11186 km/sek.

Michell skriver, at et legeme med samme vægtfylde som Solen og med en diameter som er 500 gange Solens vil have en undvigelseshastighed, der er større end lysets hastighed. Lys er ifølge Newton små partikler, som adlyder tiltrækningsloven. Lyspartiklerne vil altså falde ned igen, og legemet vil derfor ikke være synligt på afstand. Ikke desto mindre kunne man godt bevise eksistensen af et sådant usynligt legeme. Hvis legemet f.eks. er en stjerne med planeter, vil planeterne blive holdt i deres baner af Newtons tiltrækningslov. Det kunne også være at legemet dannede en dobbeltstjerne med en synlig stjerne, som så ville bevæge sig rundt om det fælles tyngdepunkt.

I dag ved vi godt, at lys ikke adlyder tiltrækningsloven. Ikke desto mindre synes jeg godt man kan sige, at Michells tanker om sorte huller foregreb de tanker fysikere i dag har om begrebet.

4. Michells undersøgelse af magnetiske kræfter.

Michell viste ved forsøg, at den kraft den ene ende af en lang magnet tiltrækker eller frastøder den ene ende af en anden lang magnet aftager med kvadratet på afstanden. Hvis man altså fordobler afstanden, bliver kraften fire gange så lille.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.