Forside Søgning Brugsanvisning Liste

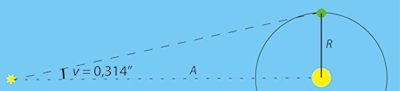
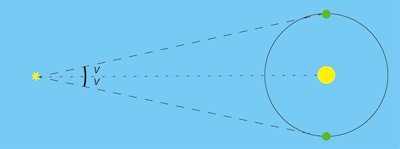
Bessels succesfulde arbejde med at bestemme afstanden til nogle stjerner er kulminationen på astronomers århundredelange arbejde om dette emne. På billedet til højre viser vi hvordan problemstillingen i virkeligheden handler om at bestemme den vinkel V, som kaldes stjernens parallakse. V er den vinkel, som Jordbanens radius ses under fra stjernen, når radius er vinkelret på afstanden til stjernen. I virkeligheden er V en meget lille vinkel, som det er svært at måle.

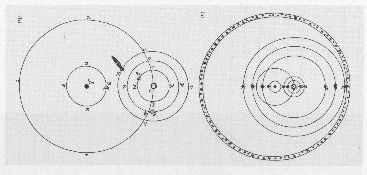Allerede i slutningen af 1500-tallet prøvede Tycho Brahe at måle parallaksen for nogle stjerner. Tycho havde på sin tid verdensrekord i astronomisk målenøjagtighed, men han måtte alligevel konstatere, at hvis der var en parallakse, så var den så lille, at stjernerne var urimeligt langt væk, så langt væk, at det kunne man på Tychos tid ikke forestille sig. Tycho måtte derfor drage den konklusion, at Jorden står stille og at Solen går rundt med de andre planeter, sådan som vi viser det på billedet til venstre.

Omkring år 1700 var Ole Rømer optaget af at finde parallaksen til nogle stjerner. Rømer forbedrede observationsnøjagtigheden, men den var stadig langt langt fra den nøjagtighed, som bestemmelse af parallakser kræver.

Den første, der med rimelig nøjagtighed bestemte nogle stjerners parallakse var Friedrich Wilhelm Bessel i 1838. I vores biografi af Bessel viser vi et billede af det observatorium som Bessel benyttede.

Den første stjerne, som Bessel fandt parallaksen for var stjernen 61-Cygni i stjernebilledet Svanen. (Cygnus er latin for stjerne.) Bessel undersøgte bevægelsen af den stjerne ved at måle variationen i dens vinkelafstand fra langt svagere nabostjerner, som sandsynligvis var meget længere væk end den lysstærke 61-Cygni. Bessel udviklede og benyttede sandsynlighedsteretiske metoder ved parallaksepestemmelsen, og nåede til det resultat, at 61-cygni har parallaksen 0,314". (1',1 bueminut er 1/60 grad og et buesekund 1" er 1/60 af et bueminut.)

Nu går vi over til at beregne afstanden A til stjernen målt i lysår. (På trods af ordet er lysår et afstandsmål, nemlig den afstand, som lyset gennemløber på et år.) Lyset er 8,3 minutter om at gå fra Solen til Jorden. Afstanden fra Jorden til Solen er derfor

R = 8,3/(60·24·365,24) = 1,62·10^-6 lysår.

Nu får vi brug for at måle vinklen V i radianer i stedet for i buesekunder, se link for oven. Da 1 radian er 57,3° er 1° = 1,75·10^-3 radianer, og et buesekund er altså 1" = 1,75·10^-3/3600 = 1,75/3,6 ·10^-6 = 0,49·10^-6. Heraf følger, at V = 0,314" = 0,314·0,49·10^-6 = 0,154·10^-6 radianer.

Da tangens til en lille vinkel målt i radianer er lig med vinklen kan man på figuren aflæse, at V =R/A, altså at afstanden

A = R/V = 10,5 lysår.

2. Bessels beskrivelse af en type usynlige objekter på himlen.

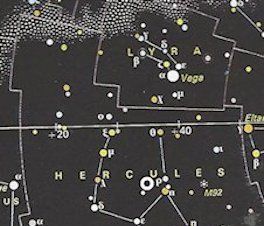På billedet til venstre viser vi et stjernekort over en omegn af stjernehimlen, der indeholder stjernebilledet Herkules. Hvis du kigger omhyggeligt ⅔ af højden under overkanten af billedet kan du se en animation af en dobbeltstjerne. De to stjerner bevæger sig i ellipseformede baner. De to ellipser har et fælles brændpunkt, som også er stjerneparrets tyngdepunkt, der ikke bevæger sig. I dag ved vi, at omtrent halvdelen af alle stjerner er dobbeltstjerner. På animationen har jeg valgt langt større banekuver end dobbeltstjerner normalt har. To stjerner på himlen, der ses tæt ved hinanden, er ikke nødvendigvis dobbeltstjerner. Når man skal afgøre om de er dobbeltstjerner, skal iagttageren observere dem over en længere periode for at se, om de virkelig bevæger sig i ellipseformede baner. Normalt kan man ikke iagttage et helt omløb, men Bessel kunne i mange tilfælde iagttage en så stor del af banerne, at han kunne beregne banernes form og størrelse. Det skete også for Bessel, at han iagttog en stjerne, der bevægede sig rundt i en ellipseformet bane, uden at han kunne se den anden halvdel af dobbeltstjernen. Men den måtte jo være der, ellers ville den iagttagne stjerne jo bevæge sig på en ret linje. Bessel kunne endda beregne visse egenskaber ved den usynlige stjerne. Årsagen kunne være, at den var så lyssvag, at den ikke kunne ses. Men der kunne også være tale om et helt nyt himmelfænomen!

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.