Ludvig August Coldings bestemmelse af varmens mekaniske ækvivalens

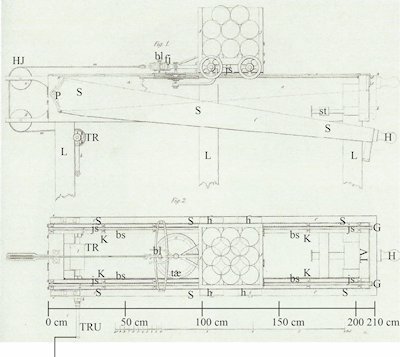
På billedet nedenfor viser vi Coldings apparat. Øverst er apparatet set fra siden, og nederst er det set ovenfra. De tydelige bogstaver har jeg skrevet ind på billedet. Apparatet er ca. 2,5 meter langt. Groft sagt består det af nogle kanonkugler, der ligger på en vogn, som man kan bevæge frem og tilbage. Vognen vejer 150 kg. Apparatet hviler på 3 lodrette søjler L, så man kan komme ind under det. Helt ude til højre er der et håndtag H, som på det øverste billede er tegnet i 2 positioner, oppe og nede. På den nederste tegning kan man se, at håndtaget sidder ud for midten af vognen, og at det sidder på en tværstang TV. Ude til siderne fortsætter denne tværstang i to lange stænger SSS, som kan dreje sig om to punkter P i den anden ende af apparatet. Stængerne er plane for oven. Til højre for det store billede viser vi et moderne billede, der giver et godt indtryk af, hvordan apparatet har set ud

2. Kørsel til højre
Højrekørslen af vognen starter, når vognen holder helt henne til venstre. Når vognen skal køres til højre, skal håndtaget H være i den øverste stilling. På tegningerne kan man se, at man kan få en understøttelse ind under tværstangen ved at skubbe stangen st ind. Så når højrekørslen startes, skal der sidde en person inde under apparatet og sørge for at skubbe st ind. st skal være trykket ind, mens vognen kører til højre på sine hjul. Hjulene kører på oversiden af stængerne SSS. I venstre side af vognen er der fastgjort en fjeder fj, og i den anden ende af fjederen starter der solidt reb. På den venstre ende af fjederen sidder der en lodret blyant bl. Den kan trykkes ned, så den tegner på den cirkulære skive, og den kan hives opad, så den ikke tegner. Rebet skal ligge løst, og vognen køres hen til højre ved et eksperimentatoren skubber til den. Det er let nok, vognen kører jo på hjulene, og der er intet nævnevædigt træk i rebet. Under kørslen til højre skal blyanten være løftet lidt, så den ikke skriver på cirkelskiven.

3. Kørsel til venstre
Lige inden for SSS stængerne og hjulene er der fastgjort 2 solide træstænger bs, de er 205 cm lange og 5 cm brede. Vi kalder dem bærestængerne. De er fastgjort oven på de lodrette stolper. Oven på dem ligger der to metalstænger js. De er ca 205 cm lange. Stængernes beliggenhed er styret af en række par af klodser K, der er fastgjort oven på bærestængerne. Klodserne er ca. ¾ cm høje. Klodserne forhindrer ikke metalstængerne i at bevæge sig i længderetningen, men de sikrer, at stængerne beholder deres position midt på bærestængerne. Klodserne kan måske dreje sig. De to metalstænger er gjort fast, meget fast, i deres højre ende. Det er der, hvor der står G. På undersiden af vognen er der lige indenfor hjulene fastgjort to træstænger. De er ca. 75 cm lange og 5 cm brede, og de ender under vognens højre ende. En tredie stang sidder også på undersiden af vognen, midt mellem de to andre. Man kan ikke se stængerne på tegningen. Den cirkelformede skive bæres af den midterste stang. På undersiden af de to yderste stænger er der omhyggeligt fastgjort metalstænger, magen til dem for oven, dog kun ca. 75 cm lange. De sidder under kanonkugledelen af vognen. Det er sådan, at når håndtaget H sænkes, så hviler metalstængerne under vognen på de lange metslstænger ms, der ligger på bærestængerne bs. Så når vognen bevæger sig mod venstre gnider de øverste metalstænger på de nederste. Under gnidningen udvikles der varme. Det er formålet med Coldings forsøg, at måle størrelsen af denne varmemængde, målt i calorier. Vognen bevæger sig lige som en slæde med meder af metal, der kører på et underlag af metal. Vognen bevæger sig under hvert forsøg 1,5 meter til venstre. Under venstrekørslen skal blyanten være trykket ned.

Nu går vi over til at beskrive, hvordan bevægelsen mod venstre vedligeholdes. På billedet til venstre kan man se, at rebet via to trisser når frem til en tredie mærket TR. Rebet er viklet nogle gange rundt om den trisse, og enden af rebet sidder fast på trissen. Trissen sidder fast på sin aksel, og på den sidder der også et håndsving, som man kan se på alle de tre figurer. Bevægelsen mod venstre vedligeholdes ved at en stærk mand drejer på håndsvinget. Hvis manden drejer med konstant drejningsmoment har fjederen konstant længde, og blyanten tegner derfor en cirkelbue på den cirkulære plade. Det beskriver vi nærmere i afsnit 5.

Trissen TR har radius 4 mm; dens omkreds er derfor 2π·4 = 25 mm. Da vognen skal køre 1,5 m = 1500 mm skal håndsvinget drejes 60 gange for at få vognen til at køre til venstre. Én omdrejning af håndsvinget flytter altså vognen 2,5 cm. Hvis vognen f.eks. er 1 minut om at køre de 1,5 m til venstre, skal håndsvinget drejes rundt en gang i sekundet. Dette resultat må være tilsigtet af Colding. Han har nok tænkt sig at stille et pendulur hen til ham, der drejer håndsvinget. Så kunne han bruge urets klikken til at kontrollere, at han drejede med en i forvejen bestemt vinkelhastighed, f.eks. en omgang på 2 sekunder.

4. Sphærometret

Når man så ved, at en stang af zink på 1 meter udvider sig 0,00011 meter når den opvarmes 1°, så kan man regne temperaturstigningen ud, når man kender længdeudvidelsen. Det fandt Rømer ud af. Læs eventuelt om det hos Rømer, der er link for oven.

Så går vi over til at beskrive hvordan længdeforøgelsen i stængerne måles, når vognen har kørt en gang til venstre. Temperaturstigningen kan naturligvis ikke bestemmes med termometre, for hvor skulle de anbringes? I stedet valgte Colding at bestemme temperaturstigningen ved at måle, hvor meget metalstængerne bliver længere. Længdeforøgelsen måles ved hjælp af et såkaldt sfærometer, som vi viser på billedet til højre. Sfærometret fastholdes på apparatet ved venstre ende af en af de lange jernstænger, sådan at når man drejer på skruen, kan man få skruens højre ende til at røre jernstangens venstre ende. Ved at dreje skruehovedet til venstre den ene vej og den anden vej bevæger skruen sig lidt (f.eks. 0,1 mm) frem og tilbage. Den lodrette cirkelskive følger med, både frem og tilbage og rundt, og den er inddelt i måske 100 lige store dele. Derfor kan man måle skrueendens placering med en nøjagtighed på 0,001 mm og endda lidt mindre. I den artikel fra 1847, som denne beskrivelse bygger på, oplyser Colding, at hvis skruen drejes én inddeling på den lodrette skala, så flytter skruens ende sig 0.0009112 mm. 9 tallet er nok rigtigt, men de sidste tre cifre tvivler jeg meget på. I en nutidig publikation vil man ikke skrive flere decimaler, end dem man kan stole på! Hvis man drejer hjulet én inddeling på den lodrette skala siger man at man har drejet det én sphærometergrad.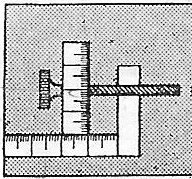

5. Den cirkulære plade
Til venstre for kanonkugledelen er der er der en cirkulær plade, der sidder fast på vognen. Faktisk er pladen et tandhjul, hvis tænder griber ind i en tandstang ved tæ. Tandstangen sidder fast på siden af den bærestang bs, som er nederst på det nederste billede. På det øverste billede kan man se hvordan tandhjulets lodrette aksel er fastgjort til vognen, både for oven og for neden. Når vognen kører fra den ene yderstilling til den anden drejer tandstangen tandhjulet lidt mere end en omgang. Under kørslen til venstre skal blyanten bl være skubbet ned, så den tegner en streg på skiven. Ideen er, at vognen det meste af vejen skal være påvirket af en konstant kraft. Hvis det er tilfældet vil fjederen have konstant længde. Derfor vil blyanten tegne en cirkelbue på den cirkulære plade, sådan som man også kan se på det nederste billede. Hvis kuven ikke er en cirkelbue er det muligt at beregne det udførte arbejde baseret på den tegnede kurve.

6. Coldings tabel. I Coldings artikel fra 1847 giver han en meget udførlig beskrivelse at de 17 forsøg, som han udførte til bestemmelse varmens mekaniske ækvivalent. Beskrivelsen findes detaljeret på den tabel, som vi viser herunder.

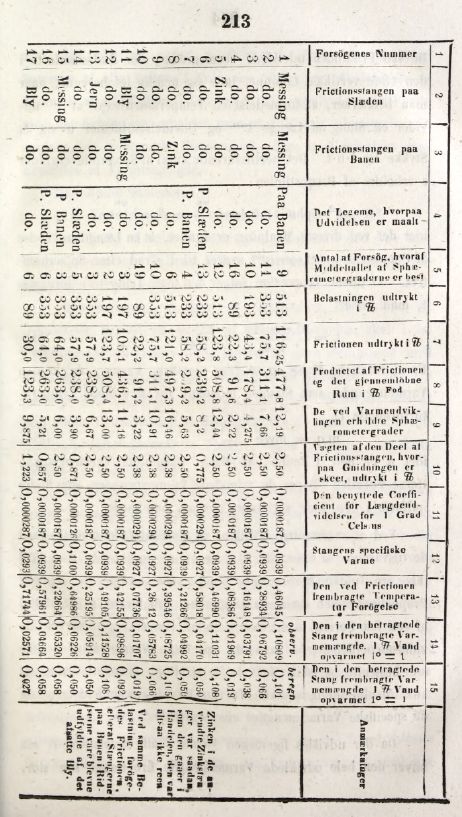. 1. Forsøgsnummer . 2. Den korte stangs materiale 3. Den lange stangs materiale . 4. Hvor er udvidelsen målt, på banen eller på slæden 5. Antallet af aflæsninger på sphærometret 6. Belastningen af vognen målt i pund 7. Trækkraften målt i pund 8. Arbejdet målt i pund·fod 9. Længdeforøgelsen målt i sphærometergrader 10. Vægten i pund af den stang, hvis længde man måler 11. Materialets længdeudvidelseskoefficient 12. Stangens varmefylde 13. Temperaturstigningen 14. Den observerede tilførte varmemængde målt i enheden 500 cal 15. Den beregnede tilførte varmemængde målt i enheden 500 cal 16. Bemærkninger

7. Det 8. forsøg
Coldings egen beskrivelse af forsøgene mærkeligt nok ingen talværdi for varmens mekaniske ækvivalent. Her beskriver jeg detaljeret det 8. forsøg (tilfældig valgt), og jeg ændrer beskrivelsen en smule, så man får en talværdi for ækvivalenten. Der er nævnt i artiklen, at det stykke slæden bevæger sig er 4,11 fod, og hvis man multiplicerer dette tal med trækkraften 132,8 får man 497,3 pundfod, som er det arbejde trækkraften udfører.

Så går vi over til at bestemme temperaturstigningen. Vi betragter nu en af de lange stænger. Hvis stangen har længdeudvidekseskoefficienten u, og længde l ved en opvarmning på t° udvide sig stykket lut. Én sphærometergrad svarer som nævnt til en længdeforøgelse på 0,0009 mm. Hvis sphærometret viser s sphærometergrader er længdeforøgelsen altså 0,0009·s. I punkt 9 af tabellen angiver tallet 16,46 antallet af sphærometergrader, som stangen har udvidet sig. Længdeudvidelsen er altså lut=16,46·0,0009 = 0,0148 mm. Udvidelseskoefficienten for zink er 0,0000294. Temperaturstigningen t er altså

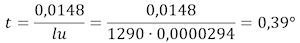
Så skal vi beregne den varmemængde i calorier, som er tilført den lange stang. Vægten af stangen er 2,38 pund = 1,19 kg = 1190 gram og den er opvarmet 0,39°. Varmefylden for Zink er 0,086 cal/gram·grad. Derfor er der tilført stangen 1190·0,39·0,086 = 39,9 cal.

Colding antager nu, at der under forsøget tilføres lige mange kalorier i alle metalstænger. (Dette omtales nærmere i biografien.) Derfor tilføres der ialt 4·39,9=160 cal. 160 cal er altså lig med 497 pundfod, og derfor er 500 cal 1553 pundfod. Dette er altså resultatet af forsøg nr.8.

Baseret på alle de beskrevne resultater kunne Colding formulere sit slutresultat på følgende måde:

Colding fandt altså, at 1 pund vand opvarmes 1°C ved et arbejde på 1185 pund·fod. Da 1 pund=0,5kg og 1fod=0,314 meter siger Colding altså, at 1 kg vand opvarmes 1°C ved et arbejde af størrelsen

1185·2·0,314=372 kg*·m. 1000 calorier er altså lig med 372 kg*m.

Nutidens resultat er, at 1000 calorier=427 kg*m. Fejlen på 55 kg*m er altså 13%, så det er ikke urimeligt langt fra det korrekte. Joule fandt omtrent samtidig med Colding resultatet 1000 cal = 424 kg*m.

Hvis man dividerer et tal i afsnit 8 med det tilsvarende tal i afsnit 9 får man 4,1 fod, som er det stykke som slæden maksimalt kan køre. Alle forsøgene foregår altså med én kørsel af slæden.

6. Afslutning

Ovenstående er baseret på to kilder. Billedet stammer fra Helge Kraghs beskrivelse i værket Natur, Nytte og Ånd fra 2005, og resten af beskrivelsen stammer fra Coldings egen artikel fra 1847. Stilen i den artikel er milevidt fra nutidens og den afviger også meget fra den form datidens fysikere valgte. Læs mere om det i biografien.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.