Joules bestemmelse af varmens mekaniske ækvivalent

1. Indledning

I en periode, der varede flere århundreder, diskuterede fysikere ivrigt hvad varmen er for noget. De fleste hældede til den anskuelse, at varme måtte være et stof, der kunne brede sig i andre stoffer, men fra slutningen af 1700-tallet bredte den opfattelse sig, at varmen er en bevægelse af små dele inde i et stof. Jo højere temperaturen i stoffet er, jo kraftigere vibrerer små partikler inde i stoffet. Især Grev Rumford støttede dette synspunkt, der er link for oven.

Lidt tidligere havde Joseph Black udført grundige kalorimeterforsøg baseret på varmeenheden 1 kalorie. En kalorie er den varmemængde der kan opvarme 1 gram vand 1°C. Black målte for eksempel hvor mange kalorier, der skal til at smelte 1 gram is, der i forvejen er opvarmet til 0°. Black kunne også finde ud af hvor mange kalorier, der skal til at opvarme 1 gram kviksølv 1°. Der er link til Black ovenfor. Såvidt jeg ved, udtalte Black sig ikke om hvad varme er for noget.

Den engelske fysiker James Prescott Joule arbejdede i mange år med at bestemme sammenhængen mellem varme og arbejde. Her beskriver vi to af de instrumenter, som Joule benyttede til bestemmelse af denne sammenhæng.

2. Måling af gnidningsvarme

På billedet til højre viser vi et apparat, som Joule brugte til at måle den varmemængde, der udvikles ved gnidning. I midten for neden står der et kalorimeter G. Det er fyldt med kviksølv. I et hul i låget på den bagerste side står der et termometer. Midt nede i kalorimetret er der to runde vandrette jernplader. Den nederste plade sidder fast, og den øverste plade er i sit centrum fastgjort på den lodrette stang, der for oven bærer et håndsving. Når man drejer på håndsvinget drejer den øverste plade altså rundt, og den presses hårdt mod den nederste af den lange, næsten vandrette vægtstang. Det fremgår ikke af figuren hvordan dette foregår, men det er vigtigt er der ikke er nævneværdig gnidning mellem vægtstangen og akslen, heller ikke når akslen roterer.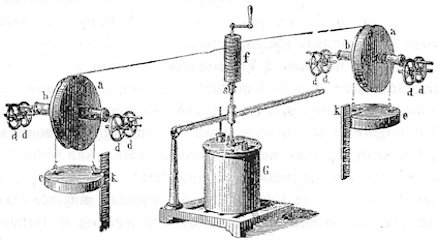

For oven er akslen tyk ved f, og dér er der viklet to snore rundt om akslen, og ude til siderne er snorene viklet flere gange rundt om de to hjul a. Snorenes ender er fastgjort på hjulene. De to hjul har tykke aksler b. De er forlænget med meget tynde aksler, der kun anes på figuren. De tynde aksler hviler på de otte hjul dd. Disse hjul drejer sig let, og der er derfor ingen nævneværdig gnidningsmodstand her, når hjulene aa drejer.

Så kommer vi til de to tunge jernplader e og e. De vejer til sammen v kg, så den samlede tyngdekraft på pladerne er v kg*. Hver af dem er ophængt vandret i to snore, der er viklet rundt om de tykke aksler b. Når man drejer den ene vej på håndsvinget går begge de to plader op, og når man drejer den anden vej, går de nedad. Højden kan aflæses på de to inddelte stænger k. På k er der markeret to positioner, en høj og en lav. Den lodrette afstand mellem de to markeringer er h meter.

Så er der en sidste meget vigtig ting. Den er markeret s, det er lige under f. Nedefra kommer der til s en tynd stang, der stikker op i en lidt tykkere stang, der kommer oppe fra håndsvinget. Det kan lade sig gøre, fordi den tykkere stang er hul, så den tynde stang kan komme op i den. Hvis man ikke gør noget andet end at dreje på håndsvinget, så forplanter drejningen sig ikke ned til kalorimetret. Nu er der ved s vandrette huller i de to stænger. Og hvis man stikker en lille stift ind gennem de tre huller, så vil drejningen af håndsvinget forplante sig ned i kalorimetret.

Vi tænker os nu, at ved forsøgets start er e pladerne i lav position, temperaturen i kalorimetret er målt, og stiften ved s er taget ud. Ved af dreje på håndsvinget bevæger vi nu de to plader stykket h opad. Herved udfører vi et arbejde af størrelsen h·v meter·kg*. Da vi har taget stiften ud, sker der under dette forløb ingen varmeudvikling i kalorimetret. Så sætter vi stiften i, og giver slip på håndsvinget. Så bevæger e - pladerne sig langsomt nedad, så langsomt, at man kan se bort fra den kinetiske energi,som pladerne har, når de er nået til bunds. Der udvikles under processen nogle få kalorier i kalorimetret. For at opnå et målbart resultat måtte Joule gentage den beskrevne proces 20 gange. Så kunne Joule måle, at der var tilført skal vi sige c kalorier til kalorimetret.

Resultatet er nu, at c cal = 20·h·v meter·kg*, og hermed er sammenhægnen mellem vameenergi og potentiel energi bestemt. Joule udførte en lang række målinger, og hans slutresultat var, at 1 kilokalorie er 424 meter·kg*.

Til ære for Joule har man senere defineret en enhed for arbejde, som kaldes 1 joule. Den defineres som det arbejde tyngdekraften udfører, når man lader et 1 kg lod falde en meter. Arbejdet er har størrelsen 1joule=1k*·1 meter. Dette arbejde er uafhængigt af hvor lang tid loddet er om at falde 1 meter. Når bevægelsesretningen falder sammen med kraftens retning, defineres arbejdet som produktet af kraften og vejen.

Kraften 1kg* afhænger en smule af hvor på Jorden eksperimentet udføres. Jeg ved ikke, hvornår fysikerne begyndte at tage hensyn til dette.

Lad os tage et eksempel: Rundetårn er 35 meter højt. Hvad sker der, hvis man oppe fra tårnet smider et lod på 1 kg ned i en beholder med 1 liter vand, der står nede på gaden. Af formlen oven for følger, at der tilføres vandet 20·35·1 = 700 kalorier. Da der skal 1000 kalorier til at opvarme 1 liter vand 1°, bliver vandet i beholderen 0,7 grader varmere. Eksemplet er ikke helt realistisk, men det giver et godt indtryk af, at der er en masse energi i varmt vand.

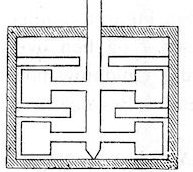Joule gentog forsøget med en ændring i kalorimetret. Han brugte vand i stedet for kviksølv, og han erstattede de to jernplader nede i kalorimetret med nogle lodrette plader, der sad fast på akslen, sådan som men kan se på billedet til venstre. Når man drejer den lodrette aksel, drejer de lodrette plader med, og det skaber uro i vandet. På indersiden af kalorimetret er der fastgjort nogle smalle lodrette plader. De forhindrer vandet i at komme i jævn rotation, så de øger den indre gnidning i vandet. Joule gentog forsøget med disse ændringer, og han må være blevet meget tilfreds, da han nåede et resultat, der lå tæt på det, han allerede havde fundet.

2. Måling af den varme der opstår ved sammentrykning af luft

Varme kan på mange forskellige måder opstå, ved at man udfører et arbejde. Vi går nu over til at beskrive Joules måling af den varmemængde, der opstår ved sammentrykning af luft. Vanskeligheden er her, at der skal udføres er meget stort arbejde for at opnå en målelig temperaturstigning. Det fremgår tydeligt af eksemplet med Rundetårn ovenfor.

På billedet til højre viser vi det apparat, som Joule brugte. Den luft, der skal sammentrykkes passerer først beholderen G. La Cour oplyser, at den er fuld af pimpstensbrokker fugtede med svovlsyre. Hvis man lader luft passere svovlsyre, fjerner syren den vanddamp, der er i luften. Derfra suges den tørre luft gennem det spiralformede rør, der befinder sig i beholderen W. W er fuld af vand, og der står et termometer i beholderen. Her sørger man for, at luften i røret får en konstant temperatur, tæt ved temperaturen i forsøgslokalet. Luften fortsætter ned i det store kalorimeter til venstre. Temmelig langt nede i kalorimetret står der en luftfyldt solid beholder R. Op fra R går der et rør C, der ender lige over kalorimetret. Der stikker en metalstang ned i det rør. Stangen har samme dimeter som rørets indvendige diameter. For oven er metalstangen takket, og den kan bevæges op og ned med håndtaget til venstre. Der står et termometer ned i kalorimetret. På det kunne Joule aflæse temperaturen med en nøjagtighed på 0,05°C.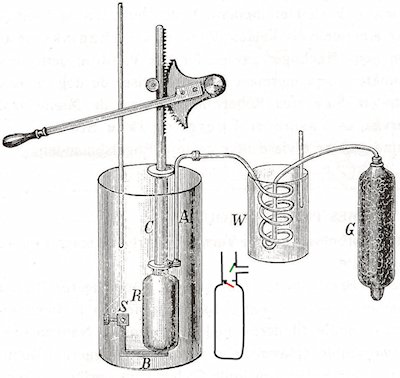

Til højre for kalorimetret har jeg suppleret LaCours figur med en tegning, der viser de to ventiler, der er lige over R. Når stangen bevæger sig nedad, lukker trykket den grønne ventil og den røde åbnes af trykket. Luften i røret bliver så presset ned i R. Når stangen bevæger sig opad lukker trykket i R den røde ventil og den grønne åbnes så stangen kan suge luft ind fra W.

Når stangen bevæges opad fra den nederste til den øverste stilling suges der et bestemt rumfang luft ved 1 atmosfæres tryk ind i røret. Og når stangen derefter med noget besvær bevæges nedad, trykkes denne luftmængde ind i R. Under denne bevægelse bliver luften opvarmet, og den udviklede varmemængde samler sig i kalorimetret. Temperaturstigningen kan imidlertid først måles, når man har bevæget stangen op og ned mange gange. Joule udførte forsøget på den måde, at han opnåede en temperaturstigning på måske et par grader. Derfor kan vi i det følgende regne temperaturen for at være konstant og bruge Boyle-Mariottes lov. Det arbejde, som udføres når stangen bevæger sig nedad er det ikke let at måle. Forskellen mellem atmosfærisk tryk og trykket i R varierer nemlig hele tiden. Lad os sige, at Joule pumpede 150 cm³ atmosfærisk luft ned i beholderen R, og at R har rumfanget 30 cm³.

Joule beregnede arbejdet med et tankeeksperiment, som vi nu går over til at beskrive.

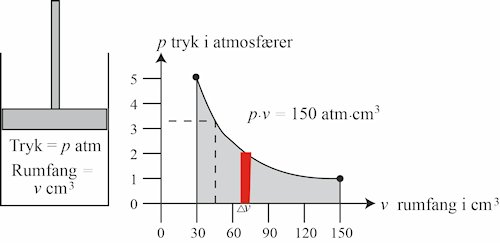Vi tænker os at sammentrykningen sker ved hjælp af et stempel, som vist på figuren til venstre. Vi måler i det følgende rumfang i cm3 og trykket i atmosfærer. Luftmængden under stemplet skal være den, som før blev sammenpresset, og trykket under stemplet starter med at være 1 atm. Rumfanget starter altså med at være 150 cm3. Når sammentrykningen er afsluttet er rumfanget 30 cm3. Tryk gange rumfang starte altså med at være 1·150, og sluttrykket bliver så ifølge Boyle-Mariottes lov 5 atm. Undervejs bevarer produktet af tryk og rumfang sin værdi, og på figuren til venstre viser vi med den sorte kurve, hvordan tryk og rumfang varierer.

De stiplede linjer viser at hvis rumfanget er 45 cm³, så er trykket 3⅓ atmosfærer. Produktet af disse to er faktisk 150. Vi går nu over til at beregne det arbejde, der udføres for at presse stemplet ned.

Vi starter med at beregne det arbejde, som skal udføres for at formindske rumfanget fra højre side af den røde figur til venstre side af den. Rumfangsformindskelsen er den viste størrelse Δv, og trykket er højden af de røde figur, som er 2 atm. Hvis vi nu tænker os, at stemplet har et tværsnitsareal på 1 cm² har rumfangsformindskelsen samme talværdi som stemplets bevægelse, så stemplet har altså bevæget sig Δv cm i den tidsperiode, det tager at passere den røde figur. Arbejdet er kraft gange vej, så arbejdet bliver størrelsen af den røde figur. Tilsvarende resultat fås for andre beliggenheder af den røde figur. Jeg siger størrelse og ikke areal, fordi der er forskellige enheder på de to akser. I mine kilder har jeg ikke fundet et eksempel, hvor arbejdets størrelse bliver beregnet, men nu går jeg over til at beregne det. Det samlede arbejde som skal udføres for at formindske rumfanget fra 150 til 30 cm³ er lig størrelsen af det grå område. Jeg har ikke kunnet finde en matematisk fremgangsmåde til bestemmelse af størrelsen af dette områdes størrelse, men nu går jeg over til at bruge en metode, der kan bestemme områdets størrelse med tilfredsstillende nøjagtighed.

På billedet til højre har det røde område med god tilnærmelse samme størrelse som det grå område ovenfor. Jeg har valgt et rødt område, der består af 4 rektangler, der står på den vandrette akse, og som såvidt muligt har samme størelse som den tilsvarende del af det grå område. F.eks. har jeg tilstræbt, at de to områder mærket x har samme størrelse, og tilsvarende for de andre søjler. Rektanglet længst til venstre har størrelsen 30·3,3 atm·cm3. På tilsvarende måde kan man behandle de andre søjler, og den samlede størrelse af det røde område er derfor S=30·(3,3+1,9+1,3+1)=225 atm·cm3 S er det arbejde der skal udføres for at formindske rumfanget fra 150 cm3 til 30 cm3.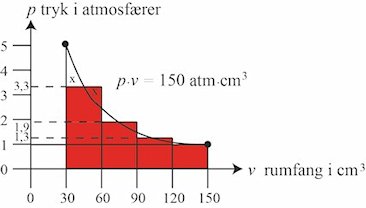

Hvis man ønsker en større nøjagtighed, kan man uden vanskelighed vælge flere og smallere søjler. Hermed har vi bestemt det arbejde, som skal udføres for at presse 150 cm³ luft sammen til et rumfang på 30 cm³, og den udviklede varmemængde kunne Joule beregne ud fra temperaturstigningen i kalorimetret. Hermed er sammenhængen mellem størrelsen af et arbejde og den tilsvarende temperaturstigning bestemt.

Af dem, der kender til den naturlige logaritmefunktion, kan størrelsen S også beregnes ved integration:

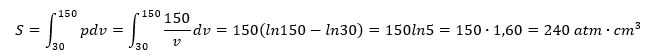
Der er en tilfredsstillende overensstemmelse mellem de to værdier af S!

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.