| Forside Søgning Brugsanvisning Liste |  |
| Ind til listen: |
Kirchhoffs teori om elektriske netværk
1. Indledning
Teorien om elektriske netværk udvikledes på baggrund af Georg Simon Ohms arbejder, som han publicerede i 1827. Ohm beviste at strømstyrken i i en ledning er proportional med spændingsforskellen v mellem ledningens ender og omvendt proptional med ledningens modstand r. Enhederne volt, ampere og modstand er valgt sådan, at v = r·i. Ohm benyttede også mere komplicerede elektriske netværk for at nå frem til sine resultater. Men det var først Kirchhoff, der udviklede en teori om elektriske netværk. Her bruger vi de nævnte enheder volt for spænding, ampere for strømstyrke og ohm for modstand.
2. Et eksempel på et elektrisk netværk
|
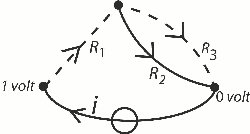
På billedet til højre viser vi et eksempel på et af de netværk, som Kirchhoff indledningsvis kunne have betragtet. Nederst til højre på billedet er der et sort punkt.
I forhold til det måles spændinger. I dag vil man sige, at punktet er jordforbundet. Nederst er der et batteri, der sikrer at spændingen i punktet nederst til venstre er 1 volt.
Med udgangspunkt i sin lov kunne Ohm have beregnet
strømme og spændinger i netværket.
Jeg beregner nu de 3 strømme uden at benytte Kirchhoffs resultater; sådan kunne Ohm også have gjort. | 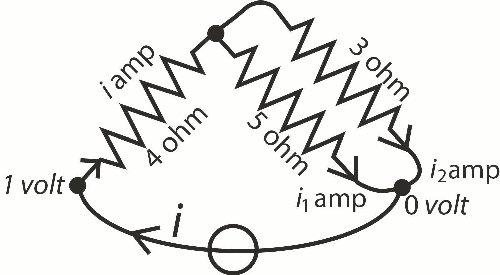 |
Læg mærke til at alle komponenter er orienterede med en pil. Strømstyrken i en komponent regnes så for positiv, hvis strømmen går i pilens retning og ellers negativ. Summen af strømmene hen til et af de sorte punkter skal så være 0; ellers ville der ophobes strøm i punktet.
Vi opstiller nu 3 ligninger, der kan bruges til bestemmelse af de tre strømme i, i1, og i2
(1) 1 = 4i + 5i1
(2) 3i2 = 5i1
(3) i = i1 + i2
Det er let at løse disse ligninger. Resultatet bliver, at
i = 8/47 amp, i1 = 3/47 amp og i2 = 5/47 amp.
Det er let at se, at disse tre tal passer i ligningerne (1), (2) og (3).
3. Et eksempel på anvendelse af Kirchhoffs netværksteori
Den metode Kirchhoff brugte, når han skulle beregne strømmen gennem en modstand i et elektrisk netværk, var helt anderledes end den vi brugte i eksemplet ovenfor. I stedet for at forudsætte at der er givet talværdier for de modstande, der findes i netværket, valgte Kirchhoff navne som R1, R2, R3, ... for modstandene i netværket, og han kunne så beregne den strøm i, som den valgte spændingsgenerator sender gennem en af modstandene bliver udtrykt ved modstandene R1, R2, R3, ...
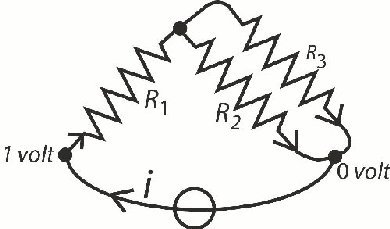
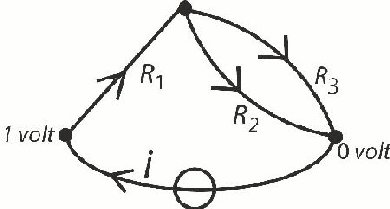
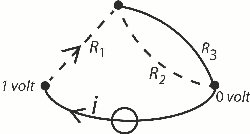
Til venstre viser vi, hvordan vi hidtil har tegnet et elektrisk netværk. Af praktiske grunde er det nu nødvendigt, at vi går over til at tegne netværket som vist til højre. Den
enkelte komponent kaldes en kant, og hver kant forbinder to punkter. Et træ i et netværk er en samling kanter med følgende egenskaber:
1. Batterikanten er med i træet.
2. Træet indeholder ikke en rundkreds af kanter.
3. Træet indeholder alle punkter i netværket.
Som man kan se minder et af disse træer om de virkelige træer. Batterikanten symboliserer træets rods overflade.
Netværket ovenfor indeholder 3 træer, nemlig iR1, iR2 og iR3. På billedet nedenfor viser vi de 3 træer
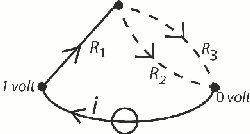
Kirchhoff beviste nu, at strømmen S i i en af modstandene udtrykkes som en brøk, S = T/N, og vi går nu over til at beskrive hvordan N beregnes. For hvert af de viste træer dannes produktet af modstandene i de kanter, der ikke er med i træet, og N er så summen af disse produkter:
N = R2R3 + R1R3 + R1R2
Læg mærke til at nævneren ikke afhænger af hvilken kant vi vil bestemme strømmen i.
Vi går nu over til at vise hvordan Kirchhoff beregnede tælleren T. Man skal finde de kredse, der indeholder både i og den kant, man skal finde strømmen i, lad os sige strømmen S i modstanden modstanden R3. Man skal så finde de kredse, der indeholder både batteriet og den kant man skal finde strømmen i. I vores tilfælde er det kun kredsen iR1R3. Tælleren er så "summen" af de modstande, der ikke er med i kredsene, altså
R2
S = 
R2R3 +
R1R3 + R1R2
Vi har nu fundet strømmen S udtrykt ved størrelserne R1, R2 og R3. Det er så nærliggende at vælge talværdier for de 3 modstande. Vi vælger R1 = 4 ohm, R2 = 5 ohm og R3 = 3 ohm, sådan som vi valgte oppe i afsnit 2. Vi indsætter nu disse værdier i ovenstående formel for S og får at S = 5/(5·3 + 4·3 + 4·5) = 5/47. Til vores glæde fik vi samme resultat som oppe i afsnit 2!
Der sker fortegnsskift afhængigt af orienteringerne af kanterne på kredsene. Det kan man let forstå, hvis man ser på den store figur herunder.
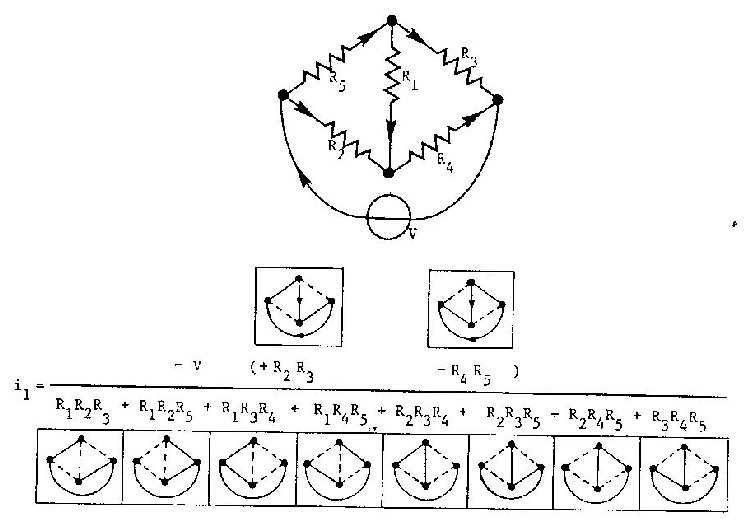
3. Afslutning
Beskrivelsen ovenfor indeholder intet bevis for at Kirchhoffs metode er korrekt. Beviset er særdeles kompliceret. Jeg (Frank Nielsen), skrev i 1995 en lærebog med titlen GRAFTEORI, -algoritmer og netværk. Den var en del af mit arbejde på DTU. Baseret på Kirchhoffs egen publikation indeholder bogen bl.a. et bevis for metodens korrekthed. Det står på siderne 240 til 350. Bogen kan lånes på en række bilioteker, Læs mere om det i vores referencer.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |