Forside Søgning Liste

Den naturvidenskabelige revolution

Newtons arbejde blev slutstenen på den epoke i naturvidenskabens historie, som i dag kaldes den naturvidenskabelige revolution. Den varede groft regnet fra ca. 1550 til ca. 1700. Denne epoke fik enorm betydning for den moderne naturvidenskab og teknologi. Her vil vi nævne de vigtigste bidragydere inden for fysikken til denne "revolution" og deres indbyrdes afhængighed. Men det bliver noget summarisk. Hvis du vil vide mere kan du foroven søge efter fysiker eller emne.

1. Kopernikus (1473-1543) Kopernikus fremsatte det kopernikanske verdensbillede, som også kaldes det heliocentriske verdensbillede (helios betyder sol): Jorden og de andre planeter går rundt om Solen. Kopernikus hævdede ikke, at planetbanerne er cirkler. Han brugte ligesom Ptolemæus epicykler til at opnå tilfredsstillende overensstemmelse med observationerne. Men han kunne klare sig med langt færre epicykler end Ptolemæus. Et vigtigt argument for det kopernikanske verdensbillede er, at det giver en meget naturlig forklaring på, at planeterne bevæger sig frem og tilbage på himlen, de "direkte og retrograde" bevægelser. Kopernikus´ hovedværk er De revolutionibus orbium coelestium, "On the Revolutions of the Celestial Spheres", "Om himmellegemernes omdrejninger". Læg mærke til, at her betyder revolutionibus (grammatisk grundform "revolutio") ikke revolution i den moderne betydning, men omløb, omdrejninger. Dette hovedværk blev først trykt i Kopernikus´ dødsår 1543, men det var det, der blev startskuddet til den naturvidenskabelige revolution. Kopernikus´ værk var meget svært at forstå, så den katolske kirke opdagede ikke med det samme, at det var "kættersk" og "farligt" for Kirken. Se nedenfor under Galilei om kirkens reaktion, og se også i biografien af Galilei, år 1600. Den faglige udvikling beskrives i "1600 Verdensbilledets historie".

2. Tycho Brahe (1546-1601) Tycho Brahe var i modsætning til Kopernikus en blændende observator, men hans observationer støttede ikke Kopernikus´ teori. Tycho mente, at hvis jorden bevæger sig, så må det kunne ses på stjernernes bevægelser: De måtte have en såkaldt parallakse, som han imidlertid ikke kunne observere. Men Tycho undervurderede afstandene til stjernerne. Man begyndte først at finde parallakser og dermed afstande til stjerner i 1839. Det var Tycho Brahe, der målte de planetpositioner, der blev grundlaget for Keplers arbejde. Tycho beviste, at kometer er himmellegemer og ikke atmosfæriske fænomener. Han fremhævede også, at stjernehimlen undergår forandringer. Han iagttog nemlig en ny stjerne, "Stella Nova". I dag ved vi, at det var en supernova. Du kan finde mere om Tychos liv og virke under 1572 Tycho Brahe.

Tychos observatorier på Hven var på den tid verdens førende forskningsinstitution; men Tycho fik også op mod 2% af statens indtægter i støtte! Det stoppede imidlertid, da Christian den 4. blev konge. I år 1600 emigrerede Tycho til Prag. I Tychos sidste år blev han assisteret af Kepler. Det sikrede kontinuiteten i astronomiens udvikling.

3. Simon Stevin (1548-1620) Tidligere havde naturvidenskabsmænd typisk været kirkelige eller adelige. Stevin kan ses som prototypen på den borgerlige videnskabsmand. Han ydede vigtige bidrag til både fysik og matematik. Han formulerede som den første kræfternes parallellogram for legemer på et skråplan, han fandt - med et vidunderligt argument - ligevægtsbetingelsen for legemer på et skråplan, og han beregnede, ved integration i klassisk forstand, hvor på en sluseport man skal trykke, for mest effektivt at holde den lukket. Han var en ivrig og succesfuld forkæmper for brugen af arabertal med 10-talssystemet og en form for decimalbrøk. Også i underholdningsbranchen havde han succes, nemlig med en sejlvogn, der kunne fare hen ad stranden med 20 passagerer. Stevin var ansat som digeingeniør i Nederlandene. I en krig mod Spanien ydede han et væsentligt bidrag ved at åbne sluser, så spanierne ikke kunne komme frem.

4. Kepler (1571-1630) Kepler skabte grundlaget for himmelens mekanik: Han fremsatte på grundlag af Tycho Brahes observationer og en tro på Kopernikus´ teori sine tre love: Keplers tre love for planeternes baner: 1. lov: "Baneloven", der siger, at banerne er ellipser med Solen i det ene brændpunkt. 2. lov: "Arealloven" beskriver, hvordan en planet bevæger sig hurtigst, når den er nærmest Solen og langsomst, når den er længst væk fra Solen. 3. lov: "Afstandsloven" siger, at når man sammenligner to planeter, da har den, der er længst væk fra Solen, længere omløbstid end den anden. Tilsammen beskriver de tre love planeternes bevægelser. For en nærmere gennemgang, se under 1609 "Keplers astronomi". Kepler designede også en astronomisk kikkert. Den har to samlelinser, og til astronomisk brug har den store fordele frem for den hollandske kikkert. Endelig var Kepler den første, der beskrev den mærkelige totalrefleksion. Den er ansvarlig for funktionen af senere tiders prismekikkerter.

5. Galilei (1564-1642) Galilei skabte grundlaget for jordens mekanik med bl.a. sine "faldlove". Se nærmere under 1600 "Galileis mekanik". Han troede ligesom Kepler på Kopernikus´ teori, og han perfektionerede to afgørende arbejdsmetoder i fysik: Observationer og eksperimenter. Galilei brugte selv de nyopfundne kikkerter og mikroskoper til observationer. Bl.a. fandt han ved hjælp af sin kikkert ud af, at planeten Jupiter har måner, der går rundt om Jupiter selv, og det benyttede han til støtte for Kopernikus´ verdensbillede. Han foretog også eksperimenter med kugler, der trillede skråt ned ad bakke ("skråplaner"). Under disse målinger skulle Galilei måle hvor lang tid kuglen var om at komme ned ad skråplanet. Han brugte bl.a. pulsen hos en tilskuer. Tilskueren blev forhåbentlig ikke alt for ophidset af forsøgene! En bedre metode, som Galilei også brugte, var at bruge et penduls svingninger. Det gik bedre, og Galilei blev så opmuntret af disse forsøg, at han tegnede et ur, der blev styret af et svingende pendul. Han fik det nu ikke udført i praksis, det gjorde Huygens senere. Men ideen var altså Galileis. Matematisk modellering, dvs. matematiske beregninger af fysiske fænomener ud fra en abstrakt model. Ordene model og modellering er dog først blevet brugt i denne sammenhæng i vor tid. Galilei lavede modeller for både det frie fald og for det skrå kast. Galileis udtryksform var klassisk græsk. Det moderne matematiske formelsprog var endnu ikke skabt.

6. Kopernikus, Galilei og den katolske kirke For nærmere detaljer, se i biografien om Galilei. - Over for Galilei hævdede den katolske kirkes repræsentanter det synspunkt, at når Gud havde skabt Jorden og mennesket på Jorden, så måtte Jorden være universets centrum. Derfor var det kætteri at hævde, at Jorden går rundt om Solen. For Kirken mente, at når noget står i Bibelen, så må det være den endegyldige sandhed. -Sandt at sige, står der intet i Bibelen om verdens centrum. Men det varede nogen tid, inden den katolske kirke opdagede, at det kopernikanske verdensbillede var "farligt". Galilei var som så mange andre astronomer tilhænger af Kopernikus´ nye verdensbillede, men han skrev populært og på folkesproget italiensk, ikke på de lærdes sprog latin. Det var helt bevidst, for han ønskede at udbrede kendskabet til det nye verdensbillede til mange mennesker. Hans populære skrifter indeholdt desuden ikke så meget matematik, som andre samtidige forskeres værker. De var lettilgængelige og forståelige for almindelige mennesker (- der kunne læse). Derfor blev Galilei "farlig" for den katolske kirke. Inkvisitionsdomstolen anklagede og dømte derfor Galilei, endda to gange: I 1615/16 og i 1633. Det er Galilei til højre på billedet.

Det var i en eller anden udstrækning medvirkende til kirkens modstand mod Galilei, at han var stridbar af sind, og at han kunne være provokerende. Både i samtiden og i dag bebrejdes Galilei for hans arrogance. Men den var nu mest rettet mod Kirken som magtfaktor. Galilei ville ikke have, at Kirken skulle diktere det fysiske verdensbillede så det stred mod fysikernes og astronomernes resultater.

Men ellers var Galilei en dybt troende katolik. Man må også tænke på, at i denne historiske periode var der først den protestantiske reformations oprør mod den katolske moderkirke. Siden svarede den katolske kirke igen med modreformationen. Så det var en tid fuld af religiøse splittelser og kampe. Og den katolske kirke havde ikke brug for ekstra kampfronter. På en måde åbnede retssagerne mod Galilei for yderligere konflikter. Men Kirken har nok alligevel hellere villet lukke munden på den rapkæftede Galilei, ligesom de foretrak at lukke munden på munken Bruno i 1600 ved simpelt hen at brænde ham på bålet. At Galilei så fortsatte sit arbejde med fysik og astronomi alligevel hjemme i sin husarrest, det kunne Kirken ikke forhindre. Men da han som gammel skulle have publiceret sit andet hovedværk "Matematiske Beregninger i To Nye Videnskaber", måtte han lade det trykke i Holland for at omgå censuren. Kirken kunne heller ikke forhindre Galilei i som gammel at videregive sin omfatende viden om fysik og astronomi til to unge fysikere, Torricelli og Viviani.

Når man klikker her, så kan man se de originale dokumenter (oversat til dansk) fra Galileis anden retssag i 1633. Det er fantastisk læsning. Først i 1992 fik Galilei en "undskyldning" fra den siddende pave.

7. René Descartes (1586-1650) Descartes var en overgangsfigur. Han gik ind for iagttagelsesbaserede studier, han fandt - uafhængigt af Snell - brydningsloven, og han formulerede inertiloven, uden dog at nævne noget om bevægelsens retning. De gamle grækere, bl.a. Platon, havde indenfor matematik det konstruktive synspunkt, at den virkelige verdens geometriske objekter var grimme billeder af matematikkens perfekte linier, cirkler og så videre. Descartes overførte inden for visse områder dette synspunkt til fysik. Da det f.eks. blev påpeget, at Descartes´ beskrivelse af det elastiske stød ikke stemte med virkeligheden, fandt Descartes, at det var virkelighedens fejl. I den ideelle verden måtte det være hans stødlove, der gjaldt. Et meget ukonstruktivt synspunkt. Descartes troede ikke på fjernvirkninger som tyngdekraft og magnetisme. Han mente f.eks., at der måtte være små, hårde tætliggende legemer mellem en magnet og et stykke jern et lille stykke væk. Hvordan skulle jernet ellers vide, at magneten er der? Descartes´ mest betydningsfulde bidrag til videnskaben var hans beskrivelse af koordinatsystemet, ikke helt som vores, men alligevel. I den forbindelse indførte Descartes brugen af alfabetets første bogstaver a, b, c, ... som betegnelse for konstanter og de sidste v, x, y, z som betegnelse for variable eller ubekendte. Den første brug af et bogstav som betegnelse for et tal skyldes Diofant. Senere benyttede Vieta mange bogstaver, og efter Descartes indførte Leibniz de nu anvendte betegnelser for integration og differentiation.

8. Huygens (1629-1695) Huygens ydede fremragende bidrag til både fysik, teknologi og matematik: Inden for fysik var Huygens´ betydeligste opdagelse relationen mellem brydningsforhold og lyshastighed, "Huygens Princip". Det grundlæggende argument findes endnu i dag i enhver lærebog i lyslære. Princippet forudsætter, at lys udbreder sig med endelig hastighed. Huygens blev derfor meget glad, da Rømer fandt lysets hastighed. Huygens princip peger også frem mod konstateringen af, at lys er en bølgebevægelse. Huygens skabte også en fuldstændig afrundet teori for det fuldstændig elastiske stød. Endvidere blev han klar over, at Saturn er omgivet af ringe, og han opdagede Saturns måne Titan. Huygens´ væsentligste teknologiske bedrift var penduluret. Det var foreslået af Galilei, men det var Huygens der førte tanken ud i livet. Hans ure var meget nøjagtigere end de tidligere, han opnåede en nøjagtighed på få sekunder i døgnet. Han konstruerede også astronomiske kikkerter, og gjorde sine opdagelser med dem. Han opfandt også uroen, der gjorde ure anvendelige til søs. Inden for matematik studerede Huygens cykloidernes egenskaber og skabte i den forbindelse begreberne evolut og afvikler. Han snusede lidt til Newtons og Leibniz´ differentialregning, men var lidt skuffet - kan man måske sige - over, at matematiske resultater, som det indtil hans tid havde været en bedrift at finde, nu kunne findes rutinemæssigt.

9. Ole Rømer (1644-1710) Ole Rømers vigtigste bidrag til fysikken var hans bestemmelse af lyshastigheden. Rømer var den første, der lavede overensstemmende termometre. Før Rømer havde termometrene individuelle skalaer, og det kunne man jo ikke basere en fysisk teori på. Rømers termometre var de første, der viste samme temperatur, når de var anbragt samme sted. Dermed åbnede Rømer for en ny gren af fysikken: Varmelære. Han startede selv ved at måle længdeudvidelseskoefficienten for en række metaller. Rømer var først og fremmest astronom, og som foregangsmand indenfor konstruktion af astronomiske instrumenter opfandt han meridiankredsen, han forbedrede mikrometret, og han havde observatorier udstyret med tidens bedste instrumenter. Rømer udførte også vigtige teknologiske arbejder. Hans tandhjul var de første teoribaserede maskinelementer. Han bidrog også til det enorme Marly maskineri, et vandpumpningsprojekt, der satte verdensrekord i maskinteknologi. Se under 1684 Marly. Som Kongens betroede medarbejder gennemførte han i Danmark talrige projekter til gavn for samfundsudviklingen: Gadebelysning, milepæle, sindssygeanstalter, kalenderskift, kloakering og meget andet.

10. Isaac Newton (1642-1727) Newton kombinerede Keplers og Galileis resultater og arbejdsmåder. Derved skabte Newton grundlaget for både himmelens og jordens mekanik. Newtons love bruges i dag, dvs. ca. 300 år efter, enormt meget inden for fysik og teknologi, bl.a. til beregning af satellitbaner, og dermed til vore dages TV og GPS. De tre centrale love hos Newton er følgende: A. Gravitationsloven. Den siger, at to legemer tiltrækker hinanden med en kraft. Jo mere legemerne vejer, jo større er kraften. Jo længere de to legemer er fra hinanden, jo mindre er kraften. B. Newtons 2. lov siger, at kraft er lig masse gange acceleration. Tidligere troede man, at når man påvirkede et legeme med en bestemt kraft, ville det få en bestemt hastighed. Newton siger: "Nej, det får en bestemt ændring af hastigheden." C. Newtons 3. lov: Når et legeme påvirker et andet med en kraft, så påvirker det andet det første med en lige så stor, men modsat rettet, kraft. Når f.eks. en magnet trækker i et stykke jern, så vil jernet trække lige så meget i magneten.

Newton påviste, at de tre love A, B og C gjorde det muligt, med tilfredsstillende nøjagtighed, både at beregne faldtider her på Jorden og - igen med tilfredsstillende nøjagtighed - at beregne planetpositioner. Det, Newton påviste, er naturligvis lige så rigtigt i dag, som det var dengang. Einstein opdagede, at man ved store hastigheder og med øgede krav til nøjagtighed må finde nye love. I denne forstand har Einsteins (1879-1955) relativitetsteori afløst Newtons love. Men teorien gør altså kun en målelig forskel ved "enormt store hastigheder".

Newton arbejdede også med optik. Han konstruerede det første spejlteleskop, og han opdagede, at hvidt lys er sammensat af lys af mange forskellige farver. Han arbejdede også med det interferensfænomen, som kaldes newtonringe. Der foregik på Newtons tid en intensiv diskussion om lysets natur: Er lyset en bølgebevægelse, eller er det partikler, der bevæger sig fremad i lysets retning. Huygens hældede mest til bølgeteorien, mens Newton støttede partikelteorien. Sagen blev først afgjort senere, da man blev klar over, at visse interferensfænomener kun kan forklares inden for bølgeteorien.

Newton skabte også differential- og integralregningen. De to regningsarter blev et uvurderligt hjæpemiddel i fysikkens udvikling. Leibniz fandt de to regningsarter senere, men uafhængigt af Newton. Newton var temmelig paranoid over for kritik, og derfor var han meget tilbageholdende med at publicere. Derfor kom Leibniz´ først med publikation af differential- og integralregning. De fleste af de symboler, vi i dag bruger inden for området, skyldes Leibniz, først og fremmest integraltegnet. Når man i fysik og matematik differentierer med hensyn til tiden, bruger man dog stadig Newtons symbol, en prik over den variable.

11. Newton og Kepler Da vi startede vores projekt om fysikhistorie i 2005, tog vi som pædagogisk udgangspunkt Poul la Cours ca. 100 år gamle bog om historisk fysik. Den er temmelig forældet på mange punkter, men den er mere menneskevenlig og pædagogisk end de fleste moderne bøger om fysik og fysikkens historie! Bl.a. nævnes det her, at det er muligt at lave en (synes jeg personligt) vældig sjov "frem-og-tilbage-regning" mellem Keplers tre love på den ene side og Newtons love A, B og C.

Man kan faktisk bevise, at "man kan gå fra Kepler til Newton og omvendt", dvs. at der i alt er 2x3=6 "veje" eller påstande, der skal bevises! Newton giver i sin Principia (1687) fyldestgørende beviser for 5 af de 6 påstande. Men der er én af vejene, som Newton ikke havde helt tjek på. Han prøvede dog at komme med lidt mere udførlige bevisskitser i de senere udgaver af Principia. Påstanden kaldes det omvendte Kepler-problem, og det siger følgende: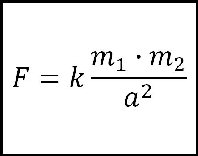

Et legeme, der bliver tiltrukket mod et fast centrum med en kraft, der er omvendt proportional med kvadratet på afstanden fra centret, må bevæge sig på et "keglesnit" (f.eks. en "ellipse"), der har det ene brændpunkt i dette center.

Påstanden bygger på Newtons gravitationslov. Newton fik ikke bevist den tilfredsstillende. På vores fysikfaglige side under 1684 "Newton om Keplers love" beskriver vi de 5 af de 6 beviser for "frem-og-tilbage-regningerne", og det er ret hård kost med mange formler. Den 6. "vej", altså beviset for dette "omvendte Kepler-problem" mangler.

Det var først schweizeren Johann Bernoulli (1667-1748), der fandt på et fuldgyldigt bevis for denne 6. "vej" i 1710. Bernoulli var en af Newtons ærkefjende Leibniz´ gode venner. Problemstillingen har helt op til vore dage givet anledning til megen forskning i fysikkens historie, se referencerne til Newton.