Forside Søgning Liste

Ole Rømers eklipsarium

Et eklipsarium er en maskine, der viser tidspunkter for sol- og måneformørkelser. I dag bruger man computere til det, men på Rømers tid måtte man klare sig med mekanismer, som en dygtig urmager kunne lave. Rømers eklipsarium blev lavet i 1680. Det var det mest udspekulerede mekaniske instrument, der var lavet indtil dette tidspunkt. Neden for beskriver vi eklipsariet, og vi forklarer hvorfor det virker. I det røde link i listen kan du læse mere om baggrunden for eklipsariet.

Først kigger man på månesiden til venstre. Når man drejer på et håndsving, som ikke er vist, drejer viseren med den lille sorte måne rundt om centrum. Samtidig varierer månens afstand fra centrum. Normalt vil månen passere over eller under markeringen for oven uden at overlappe med markeringen. Men en sjælden gang imellem er der et overlap, og hvis der er det kigger man om på kalendersiden. Der er så en solformørkelse på den dato, man kan aflæse. Forneden er der en lidt svagere markering. Hvis den lille sorte måne overlapper den, er der en måneformørkelse på den indstillede dato.

1. Astronomiske forudsætninger

For at forstå det følgende er det først og fremmest nødvendigt, at man ved hvad en synodisk måned er. En synodisk måned er 29,530589 døgn, og det er den tid der går fra en nymåne til den næste nymåne. (Vi angiver her tidsperioder i døgn og i decimalbrøk med 6 decimaler. 1 sek. er ca. 0,00001 døgn.)

A1. Fra en nymåne til den følgende fuldmåne måne går der ½ synodisk måned.

I det følgende skal vi se, at det spiller en rolle for formørkelser.

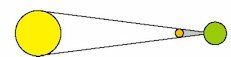
På figuren ovenfor står Månen mellem Jorden og Solen. Hvis en iagttager på Jorden står på den lille plet, hvor måneskyggen rammer Jorden, dækker Månen fuldstændig for lys fra Solen. Så er der total solformørkelse. Hvis iagttageren står lidt ved siden af pletten er der partiel formørkelse, hvor man kan se lidt af Solen. Hvis man står endnu længere væk, kan man se hele Solen. I eklipsariet skelnes der ikke mellem de to typer af solformørkelser, og der gives ingen information om, hvor på Jorden en formørkelse kan iagttages. Månen vender skyggesiden mod Jorden. Når der er en solformørkelse er det altså ved nymåne. Derfor gælder

A2. Der er et helt antal synodiske måneder mellem to solformørkelser.

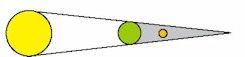
På figuren ovenfor står Jorden mellem Solen og Månen. Alle iagttagere, der står på natsiden af Jorden, ser fuldmånen formørket. Eklipsariet giver ingen information om, hvilke lande, der er på natsiden. Hvis Månen stod lidt uden for skyggen ville den være fuldt belyst på den side, der vender mod Jorden. Når der er en måneformørkelse er det altså ved fuldmåne.

A3. Fra en solformørkelse til en måneformørkelse er der derfor (x+½) synodiske måneder, hvor x er et helt tal.

Månens bane i dens bevægelse omkring Jorden er en ellipse, og Jorden er i det ene brændpunkt. Ellipsen er næsten cirkelformet, men Jorden er tydelig forskudt lidt væk fra centrum. Ellipsen ligger i en plan, der danner en vinkel på 5,1° med Jordens baneplan, der kaldes Ekliptikas plan. Skæringslinjen mellem Ekliptikas plan og månebanens plan kaldes knudelinjen. Vi viser to situationer på figuren herunder.

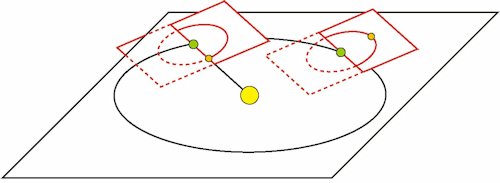
Til venstre går knudelinjen gennem Solen, og Månen står på knudelinjen og mellem Jorden og Solen. Der er derfor solformørkelse. Til højre går knudelinjen ikke gennem Solen, og der kan ikke være formørkelse, lige meget hvor på banen Månen står. Så her har vi et eksempel på en fuldmåne, hvor der ikke er en formørkelse. Hvis man iagttager situationen højt oppefra, vil det se ud som om der er en måneformørkelse, men det er der altså ikke. Hvis der er en formørkelse, vil Solen og Månen begge være tæt ved at stå på knudelinjen, og der vil omvendt være en formørkelse, når blot Solen og Månen begge begge er tæt ved at stå på knudelinjen. Til venstre kan man se, at

A4. Hvis Solen står på knudelinjen og der er fuldmåne eller nymåne, så vil der være en formørkelse.

Figuren neden for viser Jordens bane set nordfra. Månebanens storakse er vandret på figuren. Figuren viser, hvordan bevægelsen ser ud i løbet af et år. Man skal forestille sig at månebanen hælder 5,1° i forhold papirets plan, som altså er ekliptikas plan. Der er solformørkelse i startsituationen F. Fra F til den næste tegnede situation G har Månen drejet sig ca. 400° i sin bane.

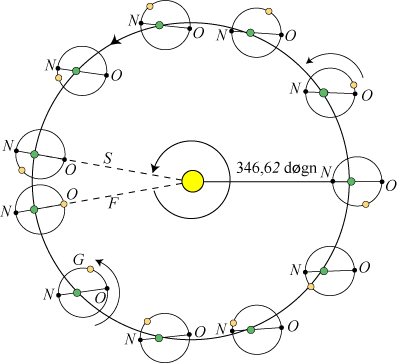Knudelinjen skærer Månens bane i knuderne. O er den opgående knude, hvor Månen kommer op over Ekliptikas plan og N er den nedgående knude. Som man ser, drejer knudelinjen sig langsomt i forhold til månebanens storakse. Da knudelinjens drejning går i modsat retning af Jordens, møder linjen fra N til O Solen igen, lidt før der er gået et år, nemlig i situationen S efter at der er forløbet et såkaldt knudeår. Længden af et knudeår er KÅ=346,620075 døgn. ½ knudeår efter startpositionen F går knudelinien igen gennem Solen, og det gør den derefter hver gang der er gået ½ knudeår: A5. Solen ligger på knudelinjen med ½ knudeårs mellemrum. Knudelinjen drejer sig på et knudeår 360° i forhold til linjen mellem Solen og Jorden.

Både Jorden og Månen bevæger sig lidt uregelmæssigt. Derfor er de understregede udsagn ikke helt rigtige, men de er dog særdeles gode tilnærmelser. Når vi her og i det følgende afsnit refererer til "virkeligheden", forudsætter vi at A1 - A5 er opfyldte.

Der var en solformørkelse den 16/12-1694. Det tidspunkt bruger vi som starttidspunkt i det følgende. I afsnit 7 fortæller vi, hvorfor vi bruger netop denne solformørkelse.

2. Rømers formørkelsesmodel

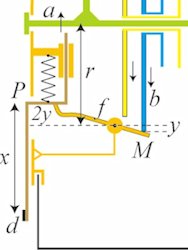
Den afgørende nøgle til forståelse af eklipsariets virkemåde er formen på den metalskive, som drejer sig inde i eklipsariet og som vi kalder baneskiven b. Den vises på figuren nedenfor.

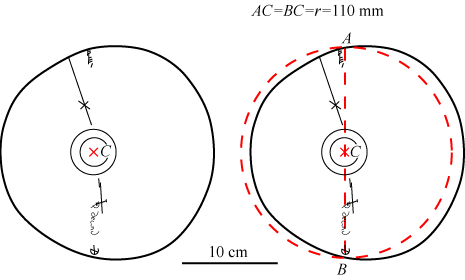
Til venstre på figuren viser vi baneskiven med de indridsninger, der findes på den. Umiddelbart kan man ikke finde nogen mening med indridsningerne og med skivens mærkelige form. Ideen med formen vises på figuren til højre. Ude på randen af skiven ligger der to punkter A og B. De ligger sådan, at midtpunktet af linjestykket AB er omdrejningscentret C, AC=BC=r=110 mm. A og B er de eneste punkter på randen, der har afstanden r fra C. Dette fremgår af den punkterede cirkel, der har centrum C og radius r. Vi tænker os, at det røde punkterede linjestykke AB er malet på baneskiven.

Før Rømer kunne gå i gang med at designe eklipsariet, måtte han vælge en mekanisk model, en model, som skulle indbygges i eklipsariet. Modellen skal i en vis udstrækning have de samme bevægelser, som dem der er i virkeligheden. Det er Rømers grundlæggende ide, at han i eklipsariet fastholder Jorden i midten og at han også fastholder linjen mellem Jorden og Solen som en lodret linje k genem Jorden. Derefter lader han eklipsariets måne og linjen AB bevæge sig i forhold til k, på samme måde som Månen og knudelinjen i virkeligheden bevæger sig i forhold til linjen mellem Jorden og Solen

Rømers model vises til højre på figuren nedenfor. Den består af en plan indeholdende følgende: En lodret linje k med tre faste punkter, nemlig Jorden J med to punkter N og Ø i afstanden r fra jordenJ og med Ø øverst. Endvidere en kurve med form som baneskiven b med punkterne A og B på randen og med det røde punkterede linjestykke AB. Baneskiven drejer sig om midtpunktet C, der ligger i J. Og endelig månen M som et punkt, der bevæger sig på randen af baneskiven.

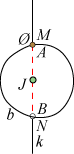
De relative bevægelser af objekterne hører med til modellen, så i modellen antager vi følgende: De relative bevægelser af objekterne hører med til modellen, så i modellen antager vi følgende:

M1. Månen passerer k med ½ synodisk måneds mellemrum, og linjen JM drejer sig jævnt om J.
M2. Månebanen b drejer sig jævnt omkring Jorden i forhold til k en gang rundt om på et knudeår, den modsatte vej af månen.

Der er også koblet et "ur" til modellen. Det viser dato, måned og kalenderår, efter gregoriansk kalender.

Hermed har vi beskrevet banerne og de relative bevægelser af de forskellige objekter. Det spiller ingen rolle

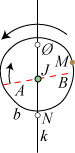
Til modellen hører også et sæt begyndelsesbetingelser. Vi kender ikke Rømers begyndelsesbetingelser, så vi vælger den oven for nævnte solformørkelse, der fandt sted den 16/12-1694 som begyndelsesbetingelse, sådan som det er vist til højre på figuren ovenfor. Den røde linje på baneskiven anbringes lodret til starttidspunktet med A øverst, og månen placeres i Ø. Eklipsariet har en måneviser. Den indgår ikke i Rømers model.

Rømers model er uventet. Solen er ikke repræsenteret i modellen, den virkelige månebane roterer ikke som her, og b ligner ikke månens bane. Det er et udtryk for Rømers evner til at følge en abstrakt, matematisk præget tankegang, at han fandt frem til denne model.

Da det røde linjestykke er lodret til at begynde med, følger det af M2 og A5 (i afsnit 1) at det også er lodret når der er en formørkelse i virkeligheden.

Når der er en solformørkelse i virkeligheden, er der ifølge A2 gået et helt antal synodiske måneder siden starten. Ifølge M1 vil eklipsariets måne stå på k og over Jorden. Da det røde liniestykke er lodret, må eklipsariets måne stå i Ø.

Når der er en måneformørkelse i virkeligheden, er der ifølge A3 gået (x + ½) synodiske måneder siden starten. Ifølge M1 vil eklipsariets måne stå på k og under Jorden. Da det røde liniestykke er lodret, må eklipsariets måne stå i N.

Vi har nu vist følgende hovedresultat:

H1: Når der er en solformørkelse i virkeligheden, vil modellens måne stå i Ø, og når der er en måneformørkelse i virkeligheden, vil modellens måne stå i N.

Nu har vi vist, at når der er en formørkelse i virkeligheden, så vises den korrekt i Ø ellet N i Rømers model. Men det ville ikke have nogen særlig værdi, hvis månen også kunne stå i Ø eller N på tidspunkter, hvor der ikke er en formørkelse. Men sådan forholder det sig heldigvis ikke. Der gælder nemlig

H2. Når eklipsariets måne står i Ø eller N, er der en formørkelse i virkeligheden.

Bevis: Når eklipsariets måne står i Ø eller N, ligger den på den lodrette linje. Der er derfor gået et helt antal halve synodiske måneder siden starten. Det er altså fuldmåne eller nymåne i virkeligheden. Når eklipsariets måne står i Ø eller N, ligger den i afstanden r fra J. Da de eneste punkter på baneskiven, der har afstanden r fra J er A og B, må den punkterede linje være lodret. Der er derfor gået et helt antal halve knudeår siden starten, og heraf følger, at Solen i virkeligheden står på knudelinjen. Af de to understregede udsagn følger som nævnt i A4, at der er en formørkelse i virkeligheden. Hermed er H2 bevist.

3. Beskrivelse af eklipsariet

Kalendersiden	Månesiden

Oven for har vi vist eklipsariets to sider. På kalendersiden til venstre er der en viser V, der peger på en af årets 365 dage. Der er også to huller.I det ene kan man se tiårene 1580, 1590,…,1770 og i det andet årene 0, 1, 2, …, 9. I de to huller kan man altså se et årstal mellem 1580 og 1779. Vi tænker os, at viseren V drejer jævnt rundt på et tropisk år, der er 365,242199 døgn. Viseren trækker de tandhjul, der viser årstallet og også maskineriet i eklipsariets indre.

Månesiden til højre er mere kompliceret. Den lyse cirkelstrimmel og området inden for den er en messingskive, der kaldes forsideskiven. Den drejer sig forbundet med viseren på bagsiden via nogle tandhjul rundt, lidt ujævnt på grund af hastighedsskiven h, en omdrejning på i gennemsnit en synodisk måned. Der er en smal revne i forsideskiven. Ud gennem den kommer der en viser, måneviseren, med en lille sort skive i spidsen. Den følges rundt med forsideskiven, men samtidig bevæger den sig lidt væk fra eller ind mod centrum, også på en uregelmæssig måde. Vi kalder den sorte spids for måneskiven d, som vi frem til afsnit 7 opfatter som et punkt.

På den yderste faste del af forsiden er der to cirkelformede markeringer. På den øverste markering vises, som vi skal se, solformørkelser, og på den nederste vises måneformørkelser. Rømers model tænkes anbragt med Jorden i forsidens centrum og med linjen k lodret. så Ø ligger over Jorden.

Vi går nu over til at beskrive, hvad der er inde i apparatet.

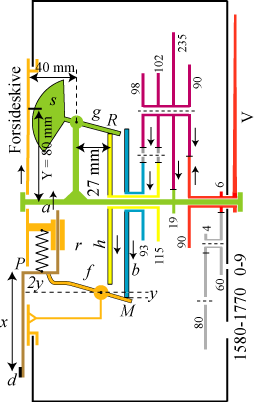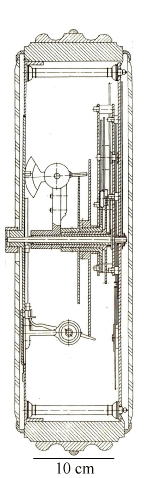Lodret snit i eklipsariet	Målfast tegning af eklipsariet

Principtegningen ovenfor til venstre viser et lodret snit gennem omdrejningsaksen på et tidspunkt, hvor viseren V er lodret. Der er 14 tandhjul. Tallene angiver antallet af tænder. Pilene viser omdrejningsretninger, når tiden går fremad. De korte vandrette streger viser, hvor tandhjul er i indgreb. De vandrette punkterede linjer er sekundære omdrejningsakser. Deres lejer sidder fast i eklipsariet. Vi tænker os, at det hele drives af den store viser V, som drejer sig jævnt en omgang om året, altså på 365,242199 døgn. De grå tandhjul nederst til højre sørger for årstallet. De to små grå tandhjul lidt over aksen tjener til at vende en omløbsretning. Alle tandhjulene drejer sig med konstant vinkelhastighed. Til højre er der en målfast tegning af eklipsariet. De to ydersider er beskyttet af glasplader.

På figuren til højre kigger vi ind i eklipsariet fra siden, forsiden er til højre. Man ser den vinkelformede skive, som er betegnet s på figuren længere oppe. s glider mellem to tætsiddene tappe, der sidder på indersiden af den gule forsideplade. På billedet kan man kun se den ene tap. Den anden ende af føleren g hviler på hastighedsskiven. Skiven s overfører via tappene den grønne aksels rotation til den gule forside. Det sker imidlertid på en noget kompliceret måde, idet s ikke ligger sådan, som man tror på tegningen. s er nemlig i forhold til skærmens plan drejet 7,2° om g. På figurerne er den øverste ende af s 6 mm nærmere iagttageren end den nederste. Under bevægelsen er dette årsag til nogle små hastighedsvariationer i bevægelsen af forsideskiven. Her antager vi, at forsideskiven drejer sig jævnt. De små variationer i drejningshastigheden, som s bevirker, vender vi tilbage til i afsnit 3. Også i Rømers model har vi set bort fra virkningen af s.

Vi vil nu redegøre for, hvordan Rømers model er indbygget i eklipsariet. Jorden er repræsenteret i forsideskivens centrum og linjen k er den lodrette linje gennem centrum. Punkterne N og Ø er ikke fysisk repræsenteret i eklipsariet, men vi tænker os, at de ligger på k i afstanden r fra Jorden. Baneskiven er den blå skive på det lodrette snit længere oppe. Månen er repræsenteret som røringspunktet M mellem baneskiven b og føleren f.

Omdrejningen af den grønne aksel, og dermed af forsideskiven, er bestemt af tandforholdet 235:19. Den grønne aksel drejer sig altså en omgang på 365,242199×19/235=29,530220 døgn, altså på en synodisk måned. Da f sidder fast på undersiden af forsideskiven, bevæger M sig jævnt en gang rundt om aksen a på en synodisk måned. Den passerer altså linjen k med ½ synodisk måneds mellemrum, så M1 er opfyldt. Føleren f presses af en fjeder ind mod baneskiven. Den blå baneskive b drejes af viseren V via tandhjulsudvekslingen 98:93. Derfor drejer den sig en omgang med konstant vinkelhastighed på 365,242199?93/98=346,607393 døgn, altså på et knudeår, så M2 er opfyldt. Det er for at opnå det, at tandtallene 93 og 98 er valgt. Der er imidlertid en fejl på ca. 15 minutter på et knudeår, og det kommenteres her. Afstanden r findes også på figuren nedenfor.

Valget af begyndelsesbetingelser i eklipsariet skal ske i overensstemmelse med begyndelsesbetingelserne i Rømers model. Vi starter altså viseren den 16. december 1694, anbringer baneskiven, så den punkterede røde linje er lodret på dette tidspunkt, og så punktet A med den Øagtige markering er øverst. Endvidere placerer vi forsideskiven, så månen M på starttidspunktet er øverst på den punkterede røde linie. Hermed er Rømers model også tidsmæssigt indbygget i eklipsariet. Da vi nu har vist, at Rømers model er indbygget i eklipsariet følger det af hovedresultaterne i afsnit 2, at

Eklipsariets måne M befinder sig i et af de tænkte punkter N eller Ø på de samme tidspunkter som dem, hvor der er en formørkelse. Når månen er i N er der måneformørkelse, og når den er i Ø er der solformørkelse.

Tilbage står så et mindre problem: Når man kigger på eklipsariet kan man ikke se eklipsariets måne. Dette problem løser Rømer ved at indbygge måneviseren d i eklipsariet, se figuren her. Vi forstiller os, at månen med føleren f flyttes, først ud til P på det lodrette snit her, og derfra videre udad med viserlængden x, sammen med måneskiven d. Da afstanden r også er følerens omdrejningspunkts afstand fra aksen flyttes de viste formørkelser lige op eller ned til P og dernæst flyttes de udad stykket x, viserlængden. Så ude i afstanden r+x fra centrum er der på linjen k anbragt to markeringscirkler, hvor formørkelserne så bliver vist. Vi bruger også navnene Ø og N om disse markeringspunkter. Markeringspunkterne kan ses på figurerne nedenfor. I det øverste vises solformørkelser og i det nederste måneformørkelser. På figuren længst til venstre, hvor det røde punkterede linjestykke er lodret, er der vist en solformørkelse.

Den punkterede cirkel har centrum C og radius r. På den næste figur viser vi hvad der sker, når månen ikke ligger på knudelinjen. Den flyttes radiært ud til d, og kommer altså ikke til at vise en formørkelse, hvad den heller ikke skal.

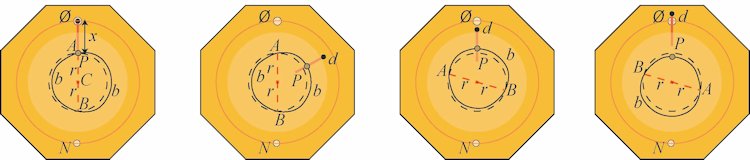
Derimod kunne man være nervøs for den situation, hvor den brune måne står på knudelinjen, men hvor der ikke er formørkelse. Sådan en situation er vist som nummer 3. Da følerarmen f, som man kan se på principtegningen her, deles i forholdet 1:2 af dens omdrejningspunkt, ligger P dobbelt så langt fra den punkterede cirkel, som månen, sådan som det er vist med y og 2y på figuren. Måneviserens længde er stykket fra den punkterede cirkel og op til markeringen. Så når måneviseren begynder i P kan den altså med sikkerhed ikke nå op til markeringscirklen.

Månen kunne også være foroven og inde i den punkterede cirkel, sådan som det er vist på figuren længst til højre. Da måneviseren præcis kan nå fra den punkterede cirkel og op til markeringen, kommer d op over markeringen når viseren begynder i P. P ligger jo dobbelt så højt over den punkterede cirkel, som månen ligger under cirklen. Vi har altså afslutningsvis følgende resultat:

Måneskiven d befinder sig i Ø, når der er en solformørkelse og ikke på andre tidspunkter, og den befinder sig i N, når der er en måneformørkelse, og ikke på andre tidspunkter.

Vi afslutter dette afsnit med at bemærke, at vi ikke er i tvivl om, at Rømer i sin planlægning af eklipsariet har fulgt samme tankegang, som vi har refereret ovenfor. F.eks. ville et eklipsarium konstrueret på baggrund af kendskab til tidligere formørkelser og en periodicitet af formørkelsestidspunkterne, have resulteret i en helt anden konstruktion af eklipsariet.

4. Hastighedsskivens betydning.

I afsnit 1 antog vi, at Månen bevæger sig jævnt. Denne antagelse er ikke helt rigtig, og det giver anledning til fejl i visningen af formørkelser. Ved en test af eklipsariet uden hastighedsskive blev der vist nogle formørkelser, som ikke var der i virkeligheden, og der var nogle virkelige formørkelser, der ikke blev vist. I virkeligheden drejer JM sig hurtigst når Månen er i perihelium, dvs. når den er nærmest Jorden, og den drejer sig langsomst, når Månen er i aphelium, dvs. når den er fjernest fra Jorden.Ved hjælp af Keplers 2. lov kan man indse, at forholdet mellem disse to vinkelhastigheder er 1,2, se her. Rømer retter delvis op på denne fejl med hastighedsskiven, der er vist på figuren nedenfor.

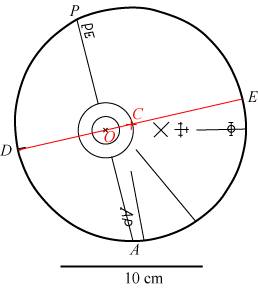Hastighedsskiven h har form som en cirkel med radius 81 mm, men det punkt C, som den drejer sig om, er forskudt 18 mm væk fra centrum. På figuren er det røde sat ind af forfatterne. Den virkelige månebane er også tilnærmet cirkelformet, men her er omdrejningspunktet (dvs Jorden) kun forskudt 8 mm væk fra centrum, hvis vi anvender samme radius. Hastighedsskiven minder altså ikke om månebanen, og det har heller ikke været Rømers hensigt. Skiven har to markeringer AP og PE, som vi fortolker som apogæum og perigæum. Om lidt skal vi begrunde, at det giver god mening. Linjen AP er vinkelret på linjen OC mellem omdrejningspunkt O og centrum C. Man kan bevise, at på hastighedsskiven er P og A de to punkter, hvor tangenten til randen danner mindst vinkel med retningen ind til O. Se beviset her. Samtidig er O midtpunkt af linjen PA og afstanden Y=CD=CE findes også inde i eklipsariet, se figuren længere nede. Følerarmen g på princip-tegningen er altså vandret, når den rører hastighedsskiven i A eller P. Her viser vi, at føleren er 27,554611 døgn om at bevæge sig en gang rundt på h.

Denne tidsperiode kaldes en anomalistisk måned, og det er den tid, der går fra Månen er i perihelium, til den igen er der. Og det er jo netop den periode, vi skal bruge, når vi skal korrigere for hastighedsvariationerne i Månens bevægelse. Føleren bevæger sig altså 360/27,55=13° i døgnet på skiven.

Når føleren bevæger sig rundt på skiven vipper følerarmen lidt frem og tilbage. Jo hurtigere den vipper, jo større korrektion giver den via skiven s til måneviserens øjeblikkelige vinkelhastighed. På figuren til højre kan man se, at hvis føleren bevæger sig lidt i omegnen af punkterne D og E vipper følerarmen ikke, så dér sker der ikke nogen hastighedskorrektion. Når følerarmen bevæger sig fra E og ned til A aftager den blå vinkel fra 90° til 77°. Og jo mindre den blå vinkel er, jo mere vil følerarmen vippe ved små bevægelser af føleren i omegnen af vinklens toppunkt. Som ovenfor nævnt er den blå vinkel mindst i punktet A; der er den 77°. Når følerarmen bevæger sig videre fra A mod D vokser den blå vinkel op til 90°. Vi får altså størst korrektion af vinkelhastigheden i punktet A , og da s er drejet, så der er tale om en subtraktion, passer det med, at vinkelhastigheden skal være mindst i apogæum. På den øverste halvdel af hastighedskurven bliver der tale om en addition af vinkelhastighed, og det går som det skal, vinkelhastigheden bliver størst i perigæum og mindst i apogæum.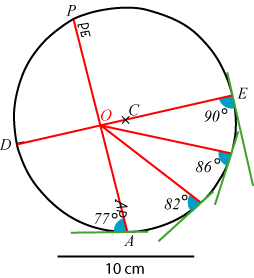

Den solformørkelse der fandt sted den 16. december 1694 valgt som begyndelsesbetingelse, fordi Månen på det tidspunkt var i perigæum. Så derfor skal hastighedsskiven på begyndelsestidspunktet anbringes sådan, at føleren g rører den i punktet P.

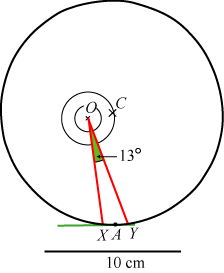Efter at vi nu kvalitativt har vist, at korrektionerne af vinkelhastigheden foregår på en fornuftig måde, går vi over til en kvantitativ vurdering. Føleren drejer sig på hastighedsskiven 13° på et døgn, og vi vælger nu et døgn hvor føleren g rører i A midt på dagen og bevæger sig fra X til Y i løbet af døgnet. Differensen mellem OY og OX er så det stykke, som føleren vipper på hastighedsskiven i løbet af dette døgn. På figuren til venstre er differensen 4 mm, og en mere højtidelig beregning, som forfatterne har udført, viser at differensen er 4,2 mm.

Figuren til højre viser den del af eklipsariet, som kommer i spil, når man skal beregne hastighedsskivens indflydelse. De tappe, som s bevæger sig imellem, er tegnet sorte. Af de mål, der er vist til venstre på figuren følger nu, at når følerrøringspunktet R flyttes 4,2 mm ind mod den grønne omdrejningsakse, da flyttes den del af s, der er mellem de to tappe 4,2×40/27 = 6,2 mm væk fra omdrejnings-aksen, altså opad. Den orange del af figuren viser, hvordan det ser ud når man ser mod forsideskivens inderside fra højre, ud mod undersiden af forsideskiven. De fire sorte cirkler til venstre er de to tappe i startsituationen og et døgn senere. Den grønne skive s ses som det grønne linjestykke, der er længst til venstre. Når det rykkes 6,2 mm opad tvinges tappene til siden, til positionen til højre, og det sker ved at forsideskiven drejer sig vinklen v mellem de punkterede linjer.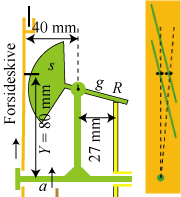

På den orange del af figuren ovenfor kan man så få øje på de trekanter, der er vist på figuren nedenfor. De 7,2° er den vinkel, som s er drejet.

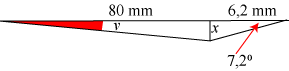
Heraf fås ved beregning, at x = 0,78 mm og videre at v = 0,5°. Uden korrek-tionen er forsidens vinkelhastighed 360/29,53 = 12,2°/døgn, og derfor bevirker korrektionen, at vinkelhastigheden i perigæum er 12,7°/døgn, mens den er 11,7°/døgn i apogæum. Forholdet mellem den maksimale og den minimale vinkelhastighed af linjen fra Jorden til månen er derfor 12,7/11,7=1,1. Det tilsvarende forhold i virkeligheden er som nævnt ovenfor 1,2. Der en fornuftig grund til, at Rømer har valgt et mindre forhold end det virkelige. Når man lader måneviseren dreje ujævnt, afviger man jo lidt fra det, vi antog i afsnit 1, og det bevirker, at man ikke kan stole helt på de to hovedresultater i afsnit 2. Vi kan altså vælge mellem to fejl: Vi kan lade månen bevæge sig ujævnt, som den gør i naturen, og miste kvalitet i hovedresultaterne, eller lade månen bevæge sig jævnt og opretholde hovedresultaterne. Her er det naturligt at formode, at Rømer ville foretrække to små fejl i stedet for én større. I hvert fald har Rømer valgt kun at korrigere hastighedsvariationerne til forholdet 1,1 i stedet for 1,2, så der er en lille fejl to steder. Som vi skal se i næste afsnit, fører denne tankegang til et fornuftigt resultat.

5. Test af eklipsariet

Da eklipsariet blev genfundet i 1982, blev det omhyggeligt istandsat. Det eneste, der ikke kunne rekonstrueres, var måneskiven d og det yderste af måneviseren. I det istandsatte eklipsarium er det altså ikke sikkert, at måneskivens diameter og måneviserens længde er korrekte. Det samme gælder derfor om den kopi af eklipsariet, som ved samme lejlighed blev lavet af urmager Søren Andersen. Bortset fra måneviseren er kopien fuldstændig magen til originalen. Forfatterne har haft fri adgang til indstille begyndelsesbetingelser og teste kopien, som nu findes på Kroppedal Museum. Formålet med denne test var dels at undersøge, hvor godt eklipsariet virker, og dels at prøve at finde ud af, hvor lang måneviseren var og hvor stor måneskivens diameter var. Det er værd at bemærke, at det er første gang i artiklen, hvor vi bruger kendskab til andre formørkelsestidspunkter end det, vi brugte som begyndelsesbetingelse.

Under testen undersøgte vi perioden fra 1687 til 1715, hvor der var 71 solformørkelser og 76 måneformørkelser. Øverst og nederst satte vi et lodret stykke tape med mm-skala på inde bag måneviseren, sådan som det er vist på billedet. Vi noterede alle de datoer, hvor måneskivens centrum lå på linjen k og mellem 178 og 210 mm fra Jorden i centrum. Derefter så vi i en formørkelsestabel, om der var en formørkelse den pågældende dato. Intervallet blev valgt, fordi alle de virkelige formørkelser blev vist i dette interval. Resultatet af testen af solformørkelserne viser vi på figuren nedenfor.

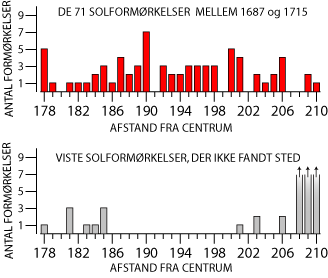F. eks. kan man af figuren se, at der var 3 solformørkelser, der vistes i afstanden 185 mm (±½ mm) over centrum. Af figuren kan man tydeligt se, at det vil være klogt at sørge for, at der ikke vises formørkelser mere end 207 mm oppe. Man går godt nok glip af 3 formørkelser, men det er prisen værd, for man slipper faktisk for 85 fejlagtige formørkelser. Forneden kan det ikke betale sig at skære noget af. Solformørkelserne siger altså, at det vil være bedst, hvis måneskivens diameter og måneviserens længde kunne vælges, så kun formørkelser intervallet fra 178 mm til 207 blev vist. Så vil 68 af de 71 solformørkelser blive vist, men der vil blive vist 14 formørkelser, der ikke fandt sted i virkeligheden.

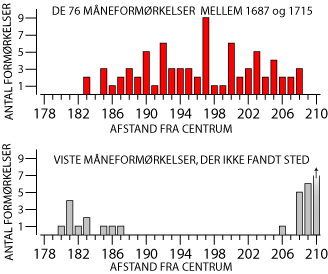Så går vi over til måneformørkelserne. Testresultatet var følgende: Alle de 76 måneformørkelser, der forekom i perioden, bliver vist korrekt i intervallet fra 183 mm til 208 mm under centrum, men på grund af fejlene vil vi tilstræbe, at kun formørkelser i intervallet fra 184 mm til 207 mm under centrum bliver vist. Så vil 71 af de 76 måneformørkelser blive vist, og der vil blive vist 4 formørkelser, der ikke fandt sted i virkeligheden.

For at bestemme hastighedsskivens indflydelse på eklipsariets pålidelighed foretog forfatterne også en test af eklipsariet, hvor hastighedsskiven var sat ud af kraft, så forsideskiven drejede sig jævnt. En iagttagelse er en situation, hvor måneskiven passerer knudelinjen mellem 178 mm og 207 mm fra centret. Resultatet af de to tests kan beskrives således:

Uden hastighedsskive: 85% af iagttagelserne er korrekt viste formørkelser. 90% af formørkelserne vises korrekt.

Med hastighedsskive: 85% af iagttagelserne er korrekt viste formørkelser. 96% af formørkelserne vises korrekt.

Det er forfatternes vurdering, at man næppe kan forvente bedre resultater af et eklipsarium fra 1680.

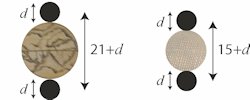
Oven for til venstre viser vi to måneskiver placeret på hver sin side af eklipsariets solformørkelsesmarkering, der har en diameter på 21 mm. Vi vil tilstræbe, at formørkelser vises, når måneskiven og solformørkelsesmarkeringen overlapper eller rører hinanden. Længden af det interval, hvor solformørkelser vises er altså 21+d mm. Ovenfor har vi bestemt intervallets længde til 29 mm og det giver, at måneskivens diameter skal være d=8 mm. Til højre på figuren vises den tilsvarende situation nede ved måneformørkelsesmarkeringen. Her får vi at 15+d=23, hvoraf d=8. Denne overensstemmelse begrunder til vores glæde størrelsesforskellen på de to markeringer. Den restaurerede måneskive, der i skrivende stund sidder i eklipsariet, er 10 mm i diameter.

Så går vi over til længden af viseren. Den skal vælges sådan, at måneskiven kan komme til at vise formørkelser i begge de to yderstillinger, der er vist på figuren. Dette opnås, ved at vælge viserlængden lig med afstanden ud til midten af de to markeringsintervaller. Midtpunktet af solmarkeringsintervallet ligger 192 mm fra centrum, og det passer fint med at midtpunktet af solformørkelsesmarkeringen ligger 191 mm fra midtpunktet. Heraf ses, at den valgte viserlængde passer fint med solformørkelserne. Specielt placerede måneskiven sig på begyndelsestidspunktet med stort overlap med markeringen for oven.

Midtpunktet af månemarkeringsintervallet ligger 195,5 mm fra centrum. Så måneformørkelsesmarkeringen burde efter vores målinger ligge 4,5 mm længere nede, så ville det passe med den foreslåede viserlængde.

Til slut bemærker vi, at det ikke vides om Rømer i denne sammenhæng har brugt tests, som vi har gjort her, eller om han har støttet sig til teoretiske overvejelser. En ting, der vil spille en rolle ved sådanne overvejelser, er retningen af baneskivens tangenter i punkterne A og B. Man vil også få brug for at vide, hvor langt fra knudepunkterne Månen kan stå, når der er en formørkelse.

Ole Rømer

Konklusionen af denne beskrivelse af eklipsariet er, at Rømers konstruktion var både elegant udtænkt og succesrig, med 96% af alle formørkelser vist korrekt. Dertil skal tilføjes, at hvis man sammenligner eklipsariet med anden samtidig mekanik, da kan der ikke herske nogen tvivl om, at dette apparat har en for sin tid meget avanceret konstruktion. Eklipsariet illustrerer på fremragende vis Rømers fine evne til at forene teori og praksis.

6. Afslutning

Som tidligere nævnt findes det originale eklipsarium på Rosenborg Slot i København; se her: http://dkks.dk/ole-roemers-rum/ . En fuldstændig dokumentation af dette apparats mekanismer, i form af et sæt originaltegninger af Poul Darnell. tegningerne findes på Kroppedal Museum i Tåstrup. Tegningslisten nedenfor viser, hvilke tegninger der eksisterer. Tegningerne er nummererede som anført nedenfor og forsynet med engelsk tekst: 1. Samlingstegning 2. Trækasse. 3. Skive med steltappe. 4. Bevægelig skive. 5. Skive og viser. 6. Bevægelig arm. 7. Diverse dele for bevægelig skive. 8. Tandhjul og drev. 9. Stelplader og tandhjul. 10. Talskiver. 11. Kurveskive for varierende vinkelhastighed. 12. Kurveskive for radiær forskydning af viser.

Til slut vil forfatterne gerne rette en tak til følgende, som har været behjælpelige med, at denne artikel kunne blive en realitet: Museumsinspektør Robert Sunderland, Kroppedal Museum, urmager, konservator Søren Andersen, cand. scient.Ivan Tafteberg Jakobsen, cand.scient. Else Høyrup samt civilingeniør Ole Henningsen, der har taget tre af fotografierne og som deltog i den tidskrævende test af eklipsariet.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.