|
Forside
Søgning
Liste |  |
Ole Rømers arbejder om varmelære
Ole Rømers arbejder om varmelære er udført, efter at han var vendt tilbage til København i 1681. De vedrørte især konstruktion af overensstemmende termometre og bestemmelse af metallers varmeudvidelse.
1. Ole Rømers arbejde med termometre
Før år 1700 var der ikke konstrueret to termometre, der stemte overens. Der var mange årsager til, at forskellige termometre ikke viste det samme. En hovedårsag var, at man ikke havde to veldefinerede fixpunkter at gå ud fra. F.eks. benyttede Fahrenheit 3 fixpunkter, af hvilke det ene var en sund mands legemstemperatur målt i armhulen. En anden fejlkilde var, at man ikke tog hensyn til, at de benyttede termometerrør ikke havde konstant tværsnitsareal.
I 1702 havde Rømer konstrueret pålidelige overensstemmende termometre. Vi beskriver nu, hvordan Rømer kan have båret sig ad.
- Først fik Rømer lavet et termometerrør af glas. Dernæst målte han omhyggeligt, hvordan
termometerrørets tværsnitsareal varierede.
Det gjorde han ved at lægge lidt kviksølv ind i termometerrøret og så måle, hvordan længden af denne lille
kviksølvsøjle varierede, når den blev placeret forskellige steder i røret. Rømer brugte kviksølv, fordi det ikke som vand eller
sprit sætter sig på rørets inderside.
Her er Rømers egen skitse af
røret med tre placeringer af kviksølvet i et konkret tilfælde:
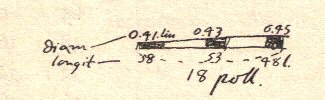
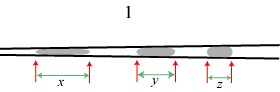
På figuren nedenfor illustrerer vi skematisk Rømers fremgangsmåde. Rømers termometerrør var tyndest i den ene ende, og de blev så nogenlunde regelmæssigt tykkere og tykkere hen mod den anden ende. Øverst viser vi tre placeringer af den samme kviksølvdråbe i røret. De tre rørstykker, der er markeret x, y og z, har altså samme rumfang
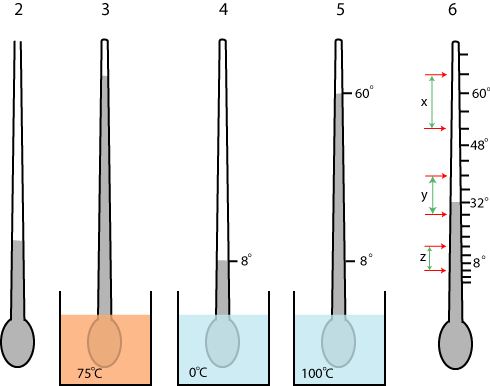
- Når det arbejde var færdigt, blev røret smeltet til i den ene ende, og der blev pustet en lille beholder. Det hele blev fyldt næsten helt med sprit.
- Dernæst blev termometret anbragt lodret, og det blev varmet kraftigt op, næsten til sprits kogepunkt. Mens det var opvarmet, blev den øverste ende smeltet til et stykke oppe over væskeoverfladen.
- Termometret blev dernæst stillet til afkøling. Under denne afkøling får spritten mindre rumfang, og der dannes et rum over spritsøjlen. I dette rum er der spritdampe. Nu er termometret fysisk færdigt og skal forsynes med en gradskala. Som det første fixpunkt valgte Rømer vands frysepunkt, som han satte til 8°.
- Som det andet fixpunkt valgte Rømer vands kogepunkt, som han satte til 60°. Rømer vidste ikke, at kogepunktet afhænger af barometerstanden. Det opdagede Fahrenheit først omkring 1720.
- Hvis røret nu havde været lige tykt hele vejen, så skulle de mellemliggende gradstreger afsættes med lige store mellemrum. I stedet afsatte Rømer nu stregerne med matematisk præcision, så der hele vejen igennem blev samme rumfang i røret mellem to på hinanden følgende grader. Det er kun hvert fjerde gradtal, der er afmærket på figuren. På figur 1 og 6 kan man se, at der skal være længere mellem gradmarkeringerne, når kviksølvdråben er lang, end når den er kort. De tre stykker x, y og z svarer hver til 12 grader Rømer. Så er termometret færdigt. To forskellige termometre med forskellig spritmængde og med forskelligt rørtværsnit, der er justeret på denne måde, er overensstemmende.
De 8° blev formodentlig valgt, fordi Rømer først havde tænkt sig at bruge temperaturen af en fryseblanding (måske is-salt-vand) som fast nulpunkt. Dette valg gav så vands frysepunkt temperaturen 8°. Senere bestemte Rømer sig til i stedet at bruge vands frysepunkt som fixpunkt, men han beholdt de 8° som gradtal for frysepunktet. Den naturlige forklaring på, at Rømer valgte tallet 60 som gradtal for vands kogepunkt, er sandsynligvis, at tallet 60 siden oldtiden havde været brugt som grundtal. Babylonerne brugte det i deres talsystem, og derfra bredte det sig ind i astronomi og matematik. Vinkelmålet en grad blev delt i 60 minutter, og en time blev også delt i 60 minutter.
I 1708 var Fahrenheit på besøg hos Rømer i København, og han lærte der, hvordan man kan lave overensstemmende termometre. Fahrenheit forstod dog ikke, at Rømer brugte vands kogepunkt som fixpunkt. At Fahrenheit lærte det af Rømer, dokumenteres af et brev fra Fahrenheit til en vis Boerhaave, dateret 17. april 1729. Du kan læse brevet her.
I vinteren 1708-1709 benyttede Rømer sine termometre til at få tegnet en kurve, der viser temperaturvariationerne i København i perioden 26. december til 26. april. Da det er verdens første temperaturkurve, viser vi den her.
Som bekendt kan man ikke sammenligne højden af Rundetårn med højden af et tordenskrald. Bl.a. derfor har man forskellige enheder for lydstyrke og længde. I den forbindelse er det tankevækkende, at ordet grad og tegnet ° begge benyttes om både vinkelmål og temperaturmål. På de fleste europæiske sprog benyttes en variant af ordet grad både om vinkelmål og temperaturmål. Denne tradition går i hvert fald tilbage til 1667, se Kirstine Meyer, 1909, p. 51 i referencerne. I Tjekkiet bruger man ordet stupeň både om temperatur og vinkelmål, og i Kina hedder begge dele du. Hvis denne tradition er verdensomspændende, tyder det meget på, at en temperaturenhed kun er fastlagt i Europa.
2. Ole Rømers arbejde med metallers længdeudvidelse ved opvarmning
Da Rømer var den første, der var i besiddelse af et pålideligt temperaturmål, var han også den første, der overhovedet var i
stand til at besvare spørgsmål om, hvordan forskellige ting afhænger af temperaturen. En af de ting, som Rømer arbejdede med,
var metallers
længdeudvidelse ved opvarmning. Han tog 7 stænger, der alle var 3 fod lange (ca. 1 meter). Stængerne var lavet af guld, kobber,
sølv, tin, bly, jern og glas.Stængernes længdeudvidelse blev målt med en "enhed" på ca.
1/7 mm. Rømer kaldte denne enhed en "del". Han
opvarmede hver stang fra 6½° til 30½°, målt på Rømers termometer, og fandt følgende længdeudvidelser målt i dele:
| Materiale | Guld | Kobber | Sølv | Tin | Bly | Jern | Glas |
| Rømers tal | 5 | 5 | 6½ | 6½ | 9½ | 3½ | 3½ |
| Moderne tal | 4,4 | 5,3 | 5,9 | 8,4 | 8,9 | 3,8 | 2,5 |
I sidste linie viser vi moderne tal for udvidelsen, stadig målt i Rømers dele. I betragtning af, at det er den første måling af sin art, synes vi, at resultaterne er imponerende.
Rømer brugte resultaterne inden for to områder: Dels studerede han temperaturens indflydelse på pendulures gang. En temperaturstigning gør penduler længere, og det bevirker, at uret går langsommere. Og så undersøgte han udvidelsens betydning for de gradskalaer, som sad på hans astronomiske instrumenter.
På Rømers tid var det matematiske formelapparat under kraftig udvikling, men Rømer brugte det næsten ikke. I hans manuskripter er der
lejlighedsvis et bogstavnavn for et tal, et rodtegn, eller en brøk med bogstaver. Når man ser hans udregninger vedrørende varmeudvidelse,
er der ingen tvivl om, at han vidste, at udvidelsen er proportional med længden, og at han formodede, at udvidelsen er proportional
med temperaturen.
I dag definerer vi et stofs længdeudvidelseskoefficient α som udvidelsen af en stang på en cm ved en grads opvarmning. Og når
vi så skal finde længden lt af en stang ved t grader, udtrykt ved længden l0 ved 0 grader,
bruger vi længdeudvidelsesformlen
Rømer regner, som om han brugte denne formel, men han er altså ikke fortrolig med formelapparatet.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |